Маршруты, цепи, циклы в графе. Связность графа. Деревья.

Маршрутом M(v0,vk) в графе называется чередующаяся последовательность вершин и ребер v0, e1, v1, e2, v2,..., ek, vk, в которой любые два соседних элемента инцидентны.

- Если v0 = vk, то маршрут замкнут, иначе открыт.

- Если все ребра различны, то маршрут называется цепью.

- Если все вершины (а значит, и ребра) различны, то маршрут называется простой цепью.

- В цепи v0, e1,..., ek, vk вершины v0 и vk называют концами цепи. Говорят, что цепь с концами u, v соединяет вершины v и u. Цепь, соединяющая вершины u и v, обозначается < u, v>.

Очевидно, что если есть цепь, соединяющая вершины u и v, то есть и простая цепь, соединяющая эти вершины.

Замкнутая цепь называется циклом.

Число циклов в графе G обозначается z(G).

Замкнутая простая цепь называется простым циклом.

Граф без циклов называется ациклическим.

Для ориентированных графов цепь называется путем, а цикл - контуром.

Граф, состоящий из простого цикла с k вершинами, обозначается Сk.

Пример:

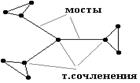
v1, v3, v1, v4 - маршрут, но не цепь;

v1, v3, v5, v2, v3, v4 - цепь, но не простая цепь;

v1, v4, v3, v2, v5 - простая цепь;

v1, v3, v5, v2, v3, v4 - цикл, но не простой цикл;

v1, v3, v4, v1 - простой цикл.

Связность

Две вершины в графе связаны, если существует соединяющая их (простая) цепь.

Граф, в котором все вершины связаны, называется связным.

Отношение связанности вершин является эквивалентностью.

Классы эквивалентности по отношению связанности называются компонентами связности графа.

Число компонент связности графа G обозначается k (G).

Граф G является связным тогда и только тогда, когда k (G) = 1.

Если k (G) > 1, то G - несвязный граф.

Граф, состоящий только из изолированных вершин (в котором k (G)= p (G) и r (G) = 0), называется вполне несвязным.

Точка сочленения / мост – это вершина / ребро, удаление которой /которого приводит к нарушению связности компонент данного графа.

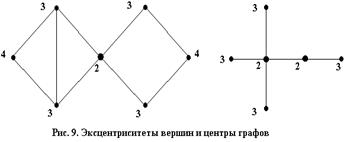
ТЕОРЕМА. Если граф G имеет р-вершин и k-компонент связности, то максимально возможное количество ребер в нем N(p, k) = ½(p - k + 1)(p - k)

Связность характеризуется:

- Числом вершинной связности (числом связности) c(G) - наименьшим количеством вершин, удаление которых приводит к несвязному или тривиальному графу.
Так, c(K1) = 0; c(Kp) = p - 1; c (Cp) = 2.

- Числом реберной связности λ(G) - минимальным количеством ребер, удаление которых приведет к несвязному графу.

В общем случае c(G) £ λ(G) £ degmin(G), где degmin(G) - минимальная степень вершин в графе.

- Рассмотрим случай λ(G) £ degmin(G):

o Если граф тривиален, следовательно, в нем нет ребер, а значит: λ(G) = deg(G) = 0.

o Если G - связный граф, то превратить его в несвязный граф можно следующим образом: найти вершины с минимальной степенью и удалить инцидентные им ребра.

- Рассмотрим случай c (G) £ λ(G):

o Для несвязных графов c = λ = 0;

o Для графа с мостом c = λ = 1.

o В общем случае c £ λ, так как удаление вершины ведет за собой удаление всех инцидентных ребер.

Расстояния между вершинами, ярусы и диаметр графа

- Длиной маршрута называется количество ребер в нем (с повторениями). Если маршрут М = v0, e1,..., ek, vk, то длина М равна k (обозначается | M | = k).

- Расстоянием между вершинами u и v (обозначается d(u, v)) называется длина кратчайшей цепи < u, v>, а сама кратчайшая цепь называется геодезической.

- Множество вершин, находящихся на одинаковом расстоянии n от вершины v (обозначение D(v, n)), называется ярусом: D(v, n) = { u Î V | d(v, u) = n }

Ясно, что всякий граф однозначно разбивается на ярусы относительно данной вершины.

- Диаметром графа G (обозначается D(G)) называется длина длиннейшей геодезической цепи.

- Обхват графа - это длина кратчайшего простого цикла.

- Окружение графа - длина максимального простого цикла.

Эксцентриситет и центр

- Эксцентриситетом e(v) вершины v в связном графе G(V, E) называется максимальное расстояние от вершины v до других вершин графа G: e(v) = max d(v, u).

Наиболее эксцентричные вершины - это концы диаметра.

- Радиусом R(G) графа G называется наименьший из эксцентриситетов вершин: R(G) = min e(v).

- Вершина v называется центральной, если ее эксцентриситет совпадает с радиусом графа, e(v) = R(G).

- Множество центральных вершин называется центром и обозначается С(G): С(G) = { v Î V | e(v) = R(G) }.

Пример:

На рис.9. указаны эксцентриситеты вершин и центры двух графов. Вершины, составляющие центр, выделены.

Деревья

- Граф без циклов называется ациклическим (или лесом).

- Дерево - это связный ациклический граф. (обозначается Tn, где n - количество вершин)

Дерево можно построить путем добавления ребер в его вершинах.

- Простейшее дерево состоит из 2 вершин, соединенных ребром.

- При добавлении очередного ребра, добавляется еще одна вершина.

o Граф G - дерево, если это связанный граф и p=q+1, где р, q - количество вершин и ребер соответственно.

o Граф G - дерево, если это ациклический граф такой, что если между двумя его вершинами провести ребро, в нем получится ровно 1 простой цикл.

o Граф G - дерево, если любые 2 его вершины соединены простой цепью.

- При введении в графе операции удаления ребра, причем такой операции, которая не приводит к нарушению связности графа, можно получить ее последовательным применением (пока возможно) остовное дерево.

- Если имеем граф с характеристиками (p, q)-граф, то для получения дерева надо удалить q – p + 1 ребро. Данное число называется циклическим рангом графа или цикломатическим числом ν(G) = q – p + 1.

- Число ν*(G)= p – 1 ребер любого остова графа G называется коциклическим рангом графа G.

ν(Tn) = 0, ν(Cn) = 1 - простой цикл,

ν(Gk) = q - p + k, ν*(Gk) = p - k,

где Gk - несвязный граф состоящий из k -компонент связности.

ТЕОРЕМА. Центр свободного дерева состоит из одной вершины или из двух смежных вершин:

z(G) = 0 & k(G) = 1 Þ C(G) = K1 Ú C(G) = K2.

Доказательство:

Для деревьев K1 и К2 утверждение теоремы очевидно.

Пусть теперь G(V, E) - некоторое свободное дерево, отличное от К1 и К2. Рассмотрим граф G'(V', E'), полученный из G удалением всех висячих вершин. Заметим, что G' - дерево, поскольку ацикличность и связность при удалении висячих вершин сохраняется.

Далее, если эксцентриситет eG(v) = d(v, u), то u - висячая вершина в дереве G. Поэтому " v Î V' eG(v) = eG' (v) + 1 и при удалении висячих вершин эксцентриситеты оставшихся уменьшаются на 1. Следовательно, при удалении висячих вершин центр не меняется, C(G) = C(G').

Поскольку дерево G конечно, то удаляя на каждом шаге все висячие вершины, в конце концов за несколько шагов придем к К1 или К2.

Теория перечисления деревьев занимается разработкой методов подсчета неизоморфных графов, обладающих данными свойствами.

Основной вопрос теории перечисления деревьев - сколько существует деревьев Тn неизоморфных друг другу.

Данная задача была решена ученым Келли. Он доказал, что всего может быть nn-2 помеченных неизоморфных деревьев. Данная теория применяется для решения задач при создании кратчайшей связной цепи.