
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 23. Средние показатели динамики временных рядов. Прогнозирование по среднему абсолютному приросту и среднему темпу роста.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Средние показатели динамики временных рядов. Средние показатели являются обобщенными характеристиками динамического ряда. Прежде всего, такой характеристикой является средний уровень ряда
где уi – отдельные уровни ряда; n – число уровней. Средний абсолютный прирост уровней рассчитывается как средняя арифметическая простая из отдельных цепных приростов:
Средний темп роста рассчитывается как средняя геометрическая из цепных темпов роста:
Темпы роста в % определяется как: Тр= Где Кi – цепные коэффициенты роста, n- число коэффициентов; у0 и уп – соответственно начальный (базисный) и конечные абсолютные уровни. Прогнозирование по среднему абсолютному приросту и среднему темпу роста. Скорость изменения уровней динамического ряда за определенный отрезок времени характеризуется средним абсолютным приростом. Полагая его стабильным, прогноз можно дать в виде следующей экстраполяции: Упр = Уб + Где Упр – прогнозируемый уровень; Уб- уровень принятый за базу экстраполяции (обычно последний уровень динамического ряда Уп; L – период упреждения. Прогноз по среднему коэффициенту роста имеет следующий вид: Упр= Уб Такие способы применимы для предварительного прогноза. Вопрос 24. Стационарные временные ряды, проверка ряда на стационарность, построение доверительного интервала для прогноза. Временной ряд называется стационарным, если в нем отсутствует тенденция развития. Это значит, что уровни динамического ряда варьируют вокруг среднего уровня, отклонения от которого представляют собой случайную колебимость. Модель такого ряда имеет следующий вид: уt= где уt – уровни динамического ряда;
Метод проверки ряда на стационарность: ряд разбиваютна две равные по времени части; вычисляются средние уровни двух этих частей. Если оказывается, что средние уровни существенно не отличаются, т.е. Расчет начинается с проверки гипотезы о равенстве дисперсий в сравниваемых группах по F- критерию Фишера: F = Так число имеющихся уровней динамического ряда, как правило ограничено, то каждая половина ряда рассматривается как малая выборка, и дисперсии в них определяются формулами:
Если фактическое значение F- критерия меньше табличного при числе степеней свободы (n1- 1) и (n2-1), то гипотеза о равенстве дисперсий принимается, п в противном случае считается, что дисперсии отличаются значимо. Далее осуществляется проверка гипотезы о равенстве средних уровней в двух группах по t-критерию Стьюдента. Если дисперсии различаются незначимо, то t- критерий рассчитывается по формуле t= n1 = n2 – число уровней в каждой половине динамического ряда;
Фактическое значение t-критерия сравнивается с табличным при уровне значимости Если проверка по F- критерию Фишера показала, что дисперсии уровней в двух половинах ряда отличаются значительно, то t- критерий Стьюдента определяется по следующей формуле: t = Полученное фактическое значение t- критерия сравнивается с табличным при числе степеней свободы (f-2), где f= Прогноз по стационарному ряду основан на предположении о неизвестности в будущем среднего уровня динамического ряда. Так отдельные уровни дин.ряда колеблются вокруг среднего значения, то прогноз принято давать в интервале
где
n- количество уровней ряда; tа, n-1 –табличное значение t-критерия Стьюдента при уровне значимости а и числе степеней свободы (n-1). Основной недостаток этого прогноза- прогноз не учитывает период упреждения.
|
|||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 792; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.94.125 (0.007 с.) |

 =
= 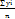 ,
, =
= 

 =
=  =
=  .
. *100,
*100, рL.
рL. ,
,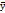 - средний за период уровень динамического ряда;
- средний за период уровень динамического ряда;
 =
=  , то ряд считается стационарным.
, то ряд считается стационарным. 12/
12/  22, где
22, где  22
22 ;
; 
 , где
, где
 = 0,05 и числе степеней свободы (п-2). Если
= 0,05 и числе степеней свободы (п-2). Если 

 , то различие средних считется незначительным и ряд считается стационарным. В противном случае гипотеза о стационарности ряда не принимается.
, то различие средних считется незначительным и ряд считается стационарным. В противном случае гипотеза о стационарности ряда не принимается. .
. При практических рассчетах, фактическое значение t-критерия оказывается меньше на 1, то групповые средние считаются равными, т.е.
При практических рассчетах, фактическое значение t-критерия оказывается меньше на 1, то групповые средние считаются равными, т.е.  =
= 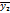 .
.
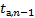
 ,
,


