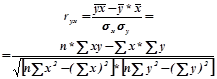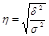Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие корреляционной зависимости. Поле корреляции. Методы выявления корреляционных связей. Коэффициент Фехнера.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Статистическая связь - это связь между величинами, при которой одна из них, случайная величина у, реагирует на изменение другой вели чины х или других величин x1, x2,…,xn (случайных или неслучайных) изменением закона распределения. Корреляционная связь - понятие более узкое, чем статистическая связь. Это частный случай статистической связи, когда разным значениям одной переменой (фактора) соответствуют разные средние значения другой переменной (результативной). При корреляционной связи изменение результативного признака не всецело зависит от факторного признака х, а лишь частично, так как возможно влияние прочих факторов Характерной особенностью корреляционных связей является то, что они проявляются не в единичных случаях, а в массе. Для того чтобы установить, есть ли зависимость между величинами, используются многообразные статистические методы. Они позволяют определить, во-первых, какие связи; во-вторых, тесноту связи (в одном случае она сильная, устойчивая, в другом слабая); в-третьих, форму связи (т.е. формулу, связывающую величину х и у).
Для выявления наличия и характера корреляционной связи используется ряд методов: рассмотрение параллельных данных (значений х и у в каждой из n единиц), графический метод, метод аналитических группировок и корреляционных таблиц, расчет коэффициентов корреляции. При небольшом числе наблюдений наличие корреляционной связи между двумя признаками х и у можно выявить путём параллельного сравнения их значений у отдельных единиц. Для этого единицы наблюдения располагают по возрастанию значений факторного признака х и затем сравнивают с ним поведение значений результативного признака у. Коэффициент Фехнера (коэффициент корреляции знаков) простейший показатель тесноты связи. Он основан на сравнении поведения отклонений индивидуальных значений каждого признака от средней величины. При этом рассматриваются не величины отклонений, а их знаки. Коэффициент Фехнера определяется по формуле Поле корреляции - это поле точек, на котором каждая точка соответствует единице совокупности: её координаты определяются значением признаков х и у. По характеру расположения точек на поле корреляции можно сделать вывод о наличии или отсутствии связи, о характере связи (линейная или нелинейная, а если линейная, то прямая или обратная).
В случае если точки корреляционного поля обнаруживают определённую направленность в своём расположении, то можно говорить о наличии связи. При этом корреляционное поле можно окантовать эллипсом (корреляционный эллипс). Метод группировок заключается в следующем. Проводится группировка единиц совокупности по факторному признаку х, и для каждой группы рассчитывается среднее значение результативного признака Таблицы взаимной сопряженности. Результаты группировки единиц совокупности могут быть оформлены в виде таблицы, в которой приведено комбинационное распределение единиц совокупности по двум признакам. Такие таблицы называются таблицами взаимной сопряженности. Если оба признака по которым дано распределение единиц совокупности, количественные, то такая таблица взаимной сопряженности называется корреляционной. 16. Линей ный коэффициент корреляции и проверка его значимости. Корреляция – это статистическая зависимость между случайными величинами, не имеющими строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой. Виды зависимостей: 1) парная корреляция – связь между двумя признаками (между двумя факторными либо между факторным и результативным признаком) 2) частная корреляция – зависимость между результативным и одним факторным признаком при фиксированном значении других факторных признаков 3) множественная корреляция – зависимость результативного и двух и более факторных признаков. Корреляционный анализ имеет своей задачей количественное определение тесноты связи между двумя признаками. Теснота связи количественно выражается величиной коэффициентов корреляции. Теснота связи при линейной зависимости измеряется с помощью линейного коэффициента корреляции:
Линейный коэффициент корреляции изменяется в пределах от -1 до+1. По степени тесноты связи различают количественные критерии оценки тесноты связи:
Теснота связи при криволинейной зависимости измеряется с помощью корреляционного отношения. Различают эмпирическое и теоретическое корреляционное отношение.
Эмпирическое корреляционное отношение:
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 1005; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.128.55 (0.007 с.) |

 :
: 
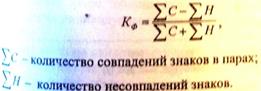
 .
.