
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Индексы Ласпейреса, Пааше и Фишера. Индекс Эджворта и их экономический смысл.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В экономике в условиях рыночных отношений особое место среди индексов качественных показателей отводится индексу потребительских цен. С его помощью осуществляется оценка динамики цен и пересчет важнейших стоимостных показателей системы национальных счетов. Рассмотрим принцип построения агрегатных индексов качественных показателей на примере индекса цен. Если нам необходимо выявить изменения цен на различные продукты и товары или количества товаров и продуктов, то необходимо привести определенное количество товаров и продуктов по определенным ценам к общей стоимости. Для этого мы должны соизмерить "вес" каждого элемента (будь то цена или кол-во товара). При отражении изменения цен на товары в качестве весов будет выступать количество товара. Если же необходимо отразить изменение количества товаров, то в роли "весов" будут выступать цены. Но возникает проблема: на уровне какого периода зафиксировать веса (базисного или отчетного). Существует два способа расчета индексов цен: индексы цен Пааше и Лайспейреса. Индекс цен Ласпейреса
Экономическое содержание Индекс цен Ласпейреса показывает, на сколько изменились цены в отчетном периоде по сравнению с базисным, но на товары реализованные в базисном периоде. Иначе говоря индекс цен Ласпейреса показывает во сколько товары базисного периода подорожали или подешевели из-за изменения цен в отчетном периоде. Индекс цен Пааше Индекс цен Пааше — это агрегатный индекс цен с весами (количество реализованного товара) в отчетном периоде.
Экономическое содержание Индекс цен Пааше характеризует изменение цен отчетного периода по сравнению с базисным по товарам, реализованным в отчетном периоде. То есть индекс цен Пааше показывает на сколько подешевели или подорожали товары. Значения индексов цена Пааше и Ласпейреса для одних и тех же данных не совпадают, так как имеют разное экономическое содержание и следовательно применяются в разных ситуациях.
В отечественной статистике до перехода к рыночным отношениям отдавали предпочтение индексу цен Пааше. Но из-за особенностей расчета начиная с 1991 года вычисление общего уровня цен на товары и услуги начали проводить по формуле Ласпейреса. Связано это с тем что во время инфляции или экономических кризисов многие товары могут выпасть из потребления. При исчислении по формуле Пааше не учитываются товары спрос на которые упал, поэтому при исчислении индекса цен по формуле Пааше небходим частый перерасчет информации для формировании правильной системы весов. В связи с этим и в международной практике прибегли к расчету индексов цен по формуле Ласпейреса. Идеальный индекс цен Фишера Представляет собой среднюю геометрическую из произведений двух агрегатных индексов цен Ласпейреса и Пааше:
Идеальность заключается в том, что индекс является обратимым во времени, то есть при перестановке базисного и отчетного периодов получается обратный индекс (величина обратная величине первоначального индекса). Индекс цен Фишера лишен какого-либо экономического содержания. В силу сложности расчета и трудности экономической интерпретации ипользуется довольно редко (например при исчислении индексов цен за длительный период времени для сглаживания значительных изменений). Эти формулы дают совершенно различное представление о соотношении уровней явления и естественно имеют разные результаты. В теории и практике статистики для решения этой проблемы применяется метод стандартных весов, который заключается в том, что значения индексируемой величины взвешиваются не по весам какого-либо одного региона, а по весам двух регионов вместе либо области, в которой эти регионы находятся. Для этого стоят индекс цен со стандартными весами Эджворта:
30. Индексы фиксированного и переменного состава. Индекс структурных сдвигов. Взаимосвязь индексов и их экономическое содержание. Будучи сводной характеристикой качественного показателя, средняя величина складывается как под влиянием значений показателя у индивидуальных элементов (единиц), из которых состоит объект, так и под влиянием соотношения их весов («структуры» объекта).
Если любой качественный индексируемый показатель обозначить через х, а его веса - через/ то динамику среднего показателя можно отразить как за счет изменения обоих факторов (х и/), так и за счет каждого фактора отдельно. В результате получим три различных индекса: • индекс переменного состава; • индекс фиксированного состава; • индекс структурных сдвигов. Индекс переменного состава отражает динамику среднего показателя (для однородной совокупности) за счет изменения индексируемой величины х у отдельных элементов (частей целого) и за счет изменения весов/, по которым взвешиваются отдельные значения х. Любой индекс переменного состава — это отношение двух средних величин для однородной совокупности (за два периода или по двум территориям): . ху0 X/, ' Х/о 'п.с (9.16) Свое название этот индекс получил потому, что он характеризует динамику средних величин не только за счет изменения индексируемой величины у отдельных элементов (частей целого), но и за счет изменения удельного веса этих частей в общей совокупности, т.е. изменения состава совокупности. Например, средняя себестоимость определенного вида продукции, выпускаемой на разных предприятиях, зависит как от уровня себестоимости на отдельных предприятиях, так и от количества продукции, выпускаемой этими предприятиями. Поэтому индекс себестоимости переменного состава отражает изменение средней себестоимости определенного продукта как за счет изменения себестоимости на каждом предприятии, так и за счет изменения удельного веса отдельных предприятий в общем выпуске продукции. Индекс фиксированного состава отражает динамику среднего показателя лишь за счет изменения индексируемой величины х, при фиксировании весов на уровне, как правило, отчетного периода /у = 2>1Л.2>аЛ Ф., • Другими словами, индекс фиксированного состава исключает влияние изменения структуры (состава) совокупности на динамику средних величин, т.е. он характеризует динамику средних величин, рассчитанных для двух периодов по одной и той же фиксированной структуре весов. По аналогии можно показать динамику среднего показателя лишь за счет изменения весов / при фиксировании индексируемой величины на уровне базисного периода х0. Такой индекс условно назван индексом структурных сдвигов (/стр): = ХУ. XV (9)8) стр 1у. 1/о Если от абсолютных весов перейти к относительным весам /. (мут следующий вид: 1 = XV). / = хм, 7 = ху. пс XV’ ф-с XV,’ стр XV' Все три формулы отражают динамику среднего показателя определенной индексируемой величины х, но в каждой из них видно, влияние какого фактора учитывается при динамике среднего показателя. Нетрудно заметить, что индекс переменного состава есть произведение индекса фиксированного состава на индекс структурных сдвигов. Таким образом, индекс структурных сдвигов можно рассчитать путем деления индекса переменного состава на индекс фиксированного состава: 'стр ' ^ф.с" Как отмечалось в параграфе 9.1, для обозначения различных показателей в индексном методе используется определенная символика. Пользуясь ею (вместо х и /), можно записать формулы индексов переменного и фиксированного составов, а также индекса структурных сдвигов для конкретных индексируемых показателей. Индекс структурных сдвигов показывает изменение средней себестоимости в зависимости только от изменения структуры (себестоимость и в числителе, и знаменателе формулы - базисная):
У Zo di А 76 v,: =?--=J™== 0,996, или 99,6%. В расчете 4,р значение числителя взято из расчета индекса постоянного состава, значение знаменателя — из расчета индекса переменного состава.,.. Индексы В отчетном периоде по сравнению с предыдущим средняя себестоимость продукции А в двух цехах снизилась на 0,4%, или на 0,02 руб. (4,76 - 4,78), за счет положительных изменений в структуре производства, т.е. возрастания доли производства цехом № 2, где уровень себестоимости и в предыдущем, и в базисном периоде ниже, чем в цехе № 1. Связь индексов переменного, постоянного состава и структурных сдвигов Индекс переменного состава, зависящий от двух факторов, равен произведению индексов, на каждый из которых влияет один фактор: Связь индексов используется для проверки расчетов и исчисления любого третьего индекса по известным двум: 0,854 «0,857-0,996. Проверку расчетов можно выполнить также, используя связь исчисленных приростов средних значений индексируемого показателя: прирост средней себестоимости за счет двух факторов равен сумме приростов за счет каждого фактора: 0,7 руб. = (0,68 + 0,02) руб. Область применения индексов переменного, постоянного состава и структурных сдвигов В статистике товарных рынков эти индексы используются для определения влияния структуры продаж определенного товара на различных рынках на изменение средней цены товара. б.б. Индексы переменного, постоянного состава и структурных сдвигов - 62,5%. В городе А уровень цены выше, чем в городе Б, следовательно, в структуре продаж произошли отрицательные изменения. _>>?1^6- 0,625+ 4 • 0,375 5,25?^4, 5-0,545 +3-0,455 "4,09 = 1,283, или 128,3%. В отчетном периоде по сравнению с базисным средняя цена картофеля в городах А и Б возросла на 28,3%, или на 1,16 руб., вследствие: 1) повышения цены в каждом городе; 2) отрицательных изменений в структуре продаж, т.е. возрастания доли продаж городом А, где уровень цены выше и в отчетном, и в базисном периодах
|
|||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 8747; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.219.213 (0.008 с.) |


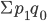 — стоимость продукции реализованной в базисном (предыдущем) периоде по ценам отчетного периода
— стоимость продукции реализованной в базисном (предыдущем) периоде по ценам отчетного периода — фактическая стоимость продукции в базисном периоде
— фактическая стоимость продукции в базисном периоде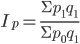
 — фактическая стоимость продукции отчетного периода
— фактическая стоимость продукции отчетного периода — стоимость товаров реализованных в отчетном периоде по ценам базисного периода
— стоимость товаров реализованных в отчетном периоде по ценам базисного периода
 .
.


