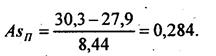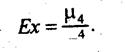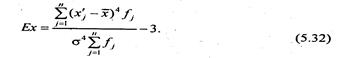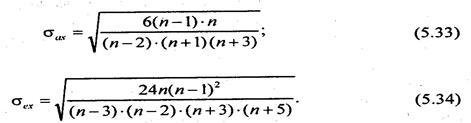Моменты распределения. Показатели формы распределения.

Центральные моменты распределения

Для дальнейшего изучения характера вариации используются средние значения разных степеней отклонений отдельных величин признака от его средней арифметической величины. Эти показатели получили название центральных моментов распределения порядка, соответствующего степени, в которую возводятся отклонения (табл. 5.7), или просто моментов (нецентральные моменты используются редко и здесь не будут рассматриваться). Величина третьего момента ц-, зависит, как и его знак, от преобладания положительных кубов отклонений над отрицательными кубами либо наоборот. При нормаль- ном и любом другом строго симметричном распределении сумма положительных кубов строго равна сумме отрицательных кубов.

 

Показатели асимметрии

На основе момента третьего порядка можно построить показатель, характеризующий степень асимметричности распределения:

 

 

As называют коэффициентом асимметрии. Он может быть рассчитан как по сгруппированным, так и по несгруппированным данным.

 

Английский статистик К. Пирсон на основе разности между средней величиной и модой предложил другой показатель асимметрии

Центральные моменты

 

По данным табл. 5.6 показатель Пирсона составил:

 

 

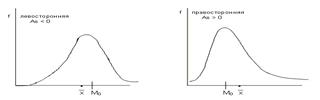
Показатель Пирсона зависит от степени асимметричности в средней части ряда распределения, а показатель асимметрии, основанный на моменте третьего порядка, - от крайних значений признака. Таким образом, в нашем примере в средней части распределения асимметрия более значительна, что видно и по графику (рис. 5.1). Распределения с сильной правосторонней и левосторонней (положительной и отрицательной) асимметрией показаны на рис. 5.3.

 

Характеристика эксцесса распределения

С помощью момента четвертого порядка характеризуется еще более сложное свойство рядов распределения, чем асимметрия, называемое эксцессом.

 

Рис. 5.3. Асимметрия, распределения

 

Показатель эксцесса рассчитывается по формуле

(5.30)

 

Часто эксцесс интерпретируется как «крутизна» распределения, но это неточно и неполно. График распределения может выглядеть сколь угодно крутым в зависимости от силы вариации признака: чем слабее вариация, тем круче кривая распределения при данном масштабе. Не говоря уже о том, что, изменяя масштабы по оси абсцисс и по оси ординат, любое распределение можно искусствен но сделать «крутым» и «пологим». Чтобы показать, в чем состоит эксцесс распределения, и правильно его интерпретировать, нужно сравнить ряды с одинаковой силой вариации (одной и той же величиной?) и разными показателями эксцесса. Чтобы не смешать эксцесс с асимметрией, все сравниваемые ряды должны быть симметричными. Такое сравнение изображено на рис. 5.4.

Рис.5.4. Эксцесс распределений

 

Для вариационного ряда с нормальным распределением значе- i ний признака показатель эксцесса, рассчитанный по формуле (5.30), j равен трем.

Однако такой показатель не следует называть термином «эксцесс», что в переводе означает «излишество». Термин «эксцесс» следует применять не к самому отношению по формуле (5.30), а к сравнению такого отношения для изучаемого распределения с величиной данного отношения нормального распределения, т.е. с величиной 3. Отсюда окончательные формулы показателя эксцесса, т.е. излишества в сравнении с нормальным распределением при той же силе вариации, имеют вид:

для ранжированного ряда

 

для интервального и дискретного вариационного ряда

 

Наличие положительного эксцесса, как и ранее отмеченного значительного различия между малым квартальным расстоянием и большим средним квадратическим отклонением, означает, что в изучаемой массе явлений существует слабо варьирующее по данному признаку «ядро», окруженное рассеянным «гало». При существенном отрицательном эксцессе такого «ядра» нет совсем.

По значениям показателей асимметрии и эксцесса распределения можно судить о близости распределения к нормальному, что бывает существенно важно для оценки результатов корреляционного и регрессионного анализа, возможностей вероятностной оценки прогнозов (см. главы 7,8,9). Распределение можно считать нормальным, а точнее говоря - не отвергать гипотезу о сходстве фактического распределения с нормальным, если показатели асимметрии и эксцесса не превышают своих двукратных средних квадратических отклонений Стц, и <т^. Эти средние квадратические отклонения вычисляются по формулам: