Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод симметричных составляющих при расчетах несимметричных КЗ.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В электрических устройствах, выполненных несимметрично, применение метода симметричных составляющих в значительной мере упрощает анализ несимметричных процессов, поскольку при этом симметричные составляющие токов связаны законом Ома с симметричными составляющими напряжений только одноименной последовательности. Другими словами, если какой–либо элемент цепи несимметричен и обладает по отношению к симметричным составляющим токов прямой (
Сопротивления Комплексная форма записи уравнений справедлива не только для установившегося режима, но и для переходного процесса, так как токи и напряжения при переходном процессе можно представить в виде проекций на соответствующую ось вращающихся и неподвижных векторов. В большинстве случаев при практических расчетах обычно учитывают лишь основные гармоники токов и напряжений. При таком ограничении представляется возможным применять метод симметричных составляющих в его обычной форме, характеризую для этого синхронную машину в схеме обратной последовательности реактивностью Протекающие по обмоткам статора токи прямой, обратной и нулевой последовательности создают магнитные потоки тех же последовательностей. Эти потоки наводят в статоре э.д.с. Вводить эти э.д.с. в расчет нецелесообразно, так как они пропорциональны токам отдельных последовательностей, значения которых необходимо определять. Поэтому в дальнейшем будем вводить в расчет только те э.д.с., которые либо известны, либо не зависят от внешних условий цепи статора (начальные значения переходной и сверхпереходной э.д.с., синхронная э.д.с. В соответствии с этим для несимметричного КЗ основные уравнения второго закона Кирхгофа для отдельных последовательностей будут иметь вид:
где
Уравнение движение ротора генератора
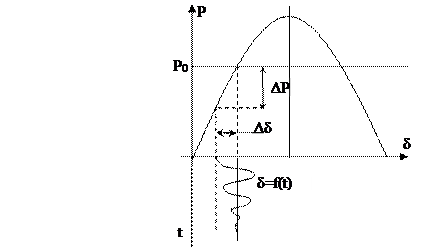
Рис. 1. К определению уравнения движения ротора СГ Пусть в результате небольшого возмущения изменился угол δ на величину Δδ<0. При этом мощность генератора уменьшится на величину ΔP. Мощность турбины P0 в первый момент времени остается неизменной и появляется избыток мощности ΔP, обусловленный разностью мощностей турбины и генератора. Избыток мощности ΔP сообщает ротору некоторое ускорение α. Значение этого ускорения пропорционально избыточной мощности ΔP и обратно пропорционально постоянной инерции Tj
где Чем больше постоянная инерции, тем медленнее растет скорость ротора под действием избыточной мощности. Ускорение α в этом уравнении представляет собой вторую производную угла δ по времени, т.е.
Что же касается величины ΔP, то она представляет собой разность между мощностью турбины и мощностью, отдаваемой генератором в сеть,
Таким образом, выражение (1) с учетом (2) и (3), можно записать в следующем виде:
Решение этого уравнения в форме δ=f(t) дает картину изменения угла во времени и позволяет установить, остается ли машина в синхронизме или под действием возрастающих колебаний угла δ выходит из синхронизма. Необходимо определить затухающий или возрастающий характер носит изменение δ во времени.
Рис. 2. К анализу изменения угла δ во времени. Сохранение устойчивости.
|
|||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 419; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.37.129 (0.007 с.) |

 ), обратной (
), обратной ( ) и нулевой (
) и нулевой ( ) последовательностей сопротивлениями
) последовательностей сопротивлениями  и
и  соответственно, то симметричные составляющие напряжений в этом элементе будут определяться как:
соответственно, то симметричные составляющие напряжений в этом элементе будут определяться как:
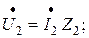

 .
.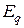 при известном токе возбуждения
при известном токе возбуждения 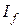 , расчетная э.д.с.
, расчетная э.д.с.  для произвольного момента времени и т.д.). Дополнительно примем, что установленные у машин устройства АРВ независимо от их конструкций реагируют только на отклонения напряжения прямой последовательности и поддерживают это напряжение на постоянном уровне.
для произвольного момента времени и т.д.). Дополнительно примем, что установленные у машин устройства АРВ независимо от их конструкций реагируют только на отклонения напряжения прямой последовательности и поддерживают это напряжение на постоянном уровне.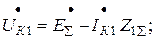


 - симметричные составляющие напряжения и тока в месте КЗ;
- симметричные составляющие напряжения и тока в месте КЗ; - результирующая э.д.с. относительно точки КЗ;
- результирующая э.д.с. относительно точки КЗ; - результирующие сопротивления схем соответствующих последовательностей относительно точки КЗ.
- результирующие сопротивления схем соответствующих последовательностей относительно точки КЗ.
 (1)
(1) - постоянная инерции.
- постоянная инерции.  .
. (2)
(2) (3)
(3)