
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет симметричных режимов работы трехфазных системСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
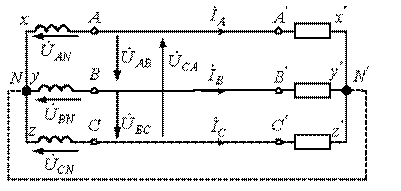
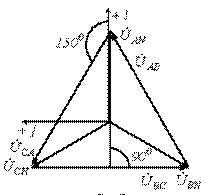
Многофазный приемник и вообще многофазная цепь называются симметричными, если в них комплексные сопротивления соответствующих фаз одинаковы, т.е. если ZA = ZB = ZC. На рис. 3.1 приведена трехфазная система при соединении фаз генератора и нагрузки в звезду. На рис. 3.2 представлена векторная диаграмма для симметричной системы напряжений.
Рис. 3.1 Рис. 3.2
Для симметричной системы напряжений соотношение между модулями линейных и фазных напряжений имеет вид
При симметричном режиме работы как трехпроводной, так и четырехпроводной трехфазной цепи фазные напряжения генератора
· фаза А · фаза В · фаза С
При соединении в звезду линейные токи
где φ определяется характером нагрузки Z, которая в нашем случае является активной, т.е. Тогда токи фаз В и С равны
При наличии нейтрального провода ток в нейтральном проводе
Расчет несимметричных режимов работы трехфазных систем Четырехпроводная цепь
Многофазный приемник называются несимметричным, если в них комплексные сопротивления соответствующих фаз не равны. При соединении фаз генератора и нагрузки в звезду и наличии нейтрального провода с нулевым сопротивлением фазные напряжения нагрузки UAN′, UBN′, UCN′ равны соответствующим напряжениям на фазах источника UAN, UBN, UCN. В этом случае фазные токи легко определяются по закону Ома, т.е. путем деления известных напряжений на фазах потребителя на соответствующие сопротивления
где ZA, ZB, ZC – комплексные сопротивления фаз нагрузки, которые в зависимости от характера нагрузки равны:
· активная нагрузка · активно-емкостная нагрузка
где Комплексные сопротивления фаз, необходимые для расчетов, в зависимости от того, в какую фазу включен конденсатор емкостью С, приведены в табл. 3.4.
Таблица 3.4
Ток в нейтральном проводе равен сумме фазных токов:
Для определения суммы фазных токов запишем их в алгебраической форме:
Складывая отдельно их действительные и мнимые части, получаем ток в нейтральном проводе в алгебраической форме записи. Для его сопоставления с результатами экспериментов переходим к показательной форме:
где
Трехпроводная цепь
При симметричном питании и несимметричной нагрузке (ZA ≠ ZB ≠ ZC) трехфазной цепи на рис. 3.3, а в общем случае будет соответствовать векторная диаграмма напряжений (см. рис. 3.3, б), на которой нейтральные точки источника и приемника занимают разные положения, т.е.
Рис. 3.3
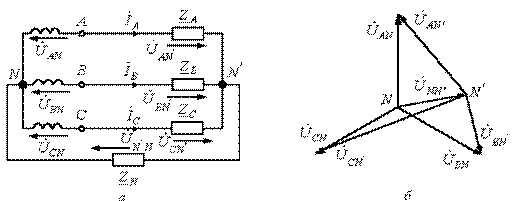
Разность потенциалов нейтральных точек генератора и нагрузки называется напряжением смещения нейтральной точки (обычно принимается, что При отсутствии нейтрального провода в трехфазной цепи для расчета напряжений на фазах нагрузки необходимо первоначально найти напряжение смещения нейтрали. Соотношение для напряжения смещения нейтрали, записанное на основании метода узловых потенциалов, имеет вид
В случае отсутствия нейтрального провода
где
где yA, yB, yC, а также φ A, φ B, φ C в зависимости от характера нагрузки могут принимать следующие значения (см. табл. 3.5): · активная нагрузка · активно-емкостная нагрузка
Таблица 3.5
Зная напряжение смещения нейтрали можно найти напряжения на фазах нагрузки:
Их вычисление удобнее проводить, имея алгебраическую форму записи напряжений на фазах генератора и смещения нейтрали:
После чего следует перейти от алгебраической формы записи фазных напряжений нагрузки к показательной. Окончательный расчет выполняется по приведенным ниже формулам. Для напряжения нагрузки фазы А:
где Аналогично можно записать выражения для определения фазных напряжений фаз В и С:
где
где Фазные токи нагрузки определяются по тем же формулам (3.4), что и в случае наличия нейтрального провода.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 582; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.192.113 (0.011 с.) |

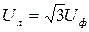 .
.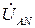 ,
, 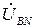 ,
, 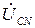 равны фазным напряжениям нагрузки
равны фазным напряжениям нагрузки 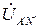 ,
, 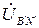 ,
, 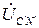 и определяются по формулам:
и определяются по формулам: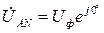 ;
;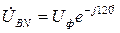 ;
;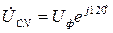 .
.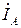 ,
, 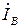 и
и 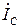 равны соответствующим фазным токам. При известных фазном напряжении и сопротивлениях фаз ZA = ZB = ZC = Z для тока фазы А можно записать
равны соответствующим фазным токам. При известных фазном напряжении и сопротивлениях фаз ZA = ZB = ZC = Z для тока фазы А можно записать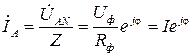 , (3.1)
, (3.1)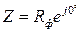 .
.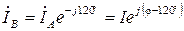 ; (3.2)
; (3.2)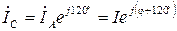 . (3.3)
. (3.3)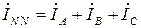 . Если система фазных токов симметрична, то
. Если система фазных токов симметрична, то 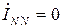 .
.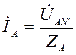 ;
; 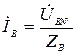 ;
; 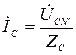 , (3.4)
, (3.4)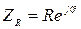 ;
;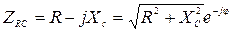 ,
,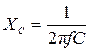 - емкостное сопротивление;
- емкостное сопротивление; 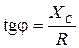 .
.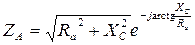
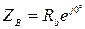
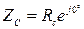
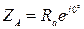
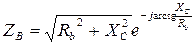
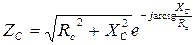
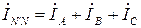 .
.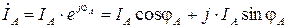 ;
;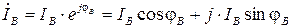 ;
;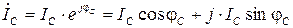 .
.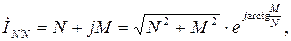 (3.5)
(3.5)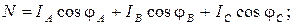
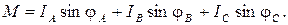
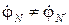 .
.
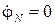 ) или просто напряжением смещения нейтрали.
) или просто напряжением смещения нейтрали.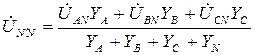 .
.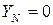 . Для расчетов формулу для напряжения смещения нейтрали удобнее представить в следующем виде
. Для расчетов формулу для напряжения смещения нейтрали удобнее представить в следующем виде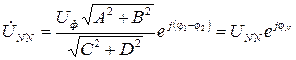 , (3.6)
, (3.6)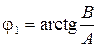 ;
; 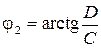 ;
;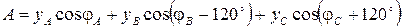 ;
;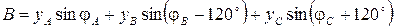 ;
;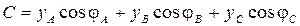 ;
;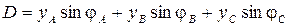 ,
,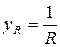 ;
; 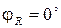 ;
;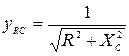 ;
; 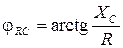 .
.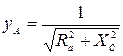 ;
; 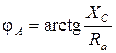
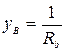 ;
; 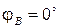
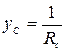 ;
; 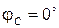
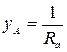 ;
; 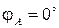
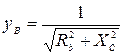 ;
; 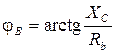
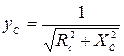 ;
; 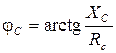
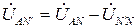 ;
; 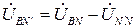 ;
; 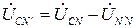 .
.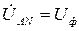 ;
;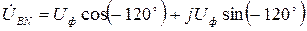 ;
;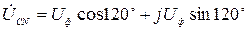 ;
;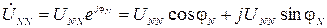 .
.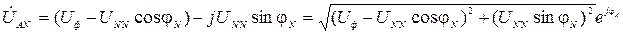 ,
,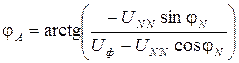 .
.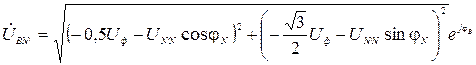 ,
,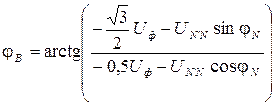 ;
;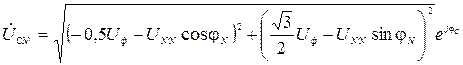 ,
,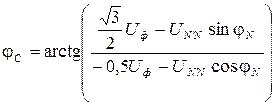 .
.


