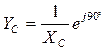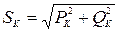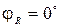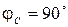Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование разветвленной электрической цепи однофазногоСодержание книги
Поиск на нашем сайте
Синусоидального тока Цель работы Ознакомиться с особенностью расчета разветвленных цепей синусоидального тока. Проанализировать цепи, содержащие параллельно соединенные активные и реактивные элементы. Содержание отчета 1. Название и цель работы. 2. Расчетная схема и исходные данные. 3. Расчетные формулы и таблица с результатами расчетов. 4. Векторная диаграмма токов и напряжений. 5. Многоугольник проводимостей.
Последовательность выполнения работы 1. Используя исходные данные, приведенные в табл. 2.1, рассчитать электрическое состояние отдельных ветвей и всей схемы, состоящей из соединенных параллельно: резистора — R; катушки — LК, RК; и конденсатора — C. Частота напряжения сети f = 50 Гц.
Таблица 2.1
Результаты расчетов занести в табл. 2.2.
Таблица 2.2
2. По результатам расчетов построить в масштабе векторную диаграмму токов и напряжений, многоугольник мощностей. Масштабы для всех отображаемых физических величин должны быть указаны.
Теоретические положения На рис. 2.1 приведена расчетная схемас параллельным соединением резистора, катушки индуктивности и конденсатора. На входе схемы действует переменное напряжение
Предварительно определяется комплексная проводимость отдельных участков цепи YR, YC и YK, содержащих соответственно резистор, конденсатор и катушку индуктивности, а также проводимость Y всей цепи, образованной параллельно соединенными элементами. С целью удобства проведения последующих вычислений следует в расчетах для каждой ветви схемы перейти от алгебраической формы записи комплексной проводимости к показательной форме, используя для этого следующие формулы:
· проводимость резистора · проводимость конденсатора где · проводимость катушки где
· проводимость схемы, содержащей параллельно соединенные резистор, конденсатор и катушку
где Ток, протекающий через отдельные участки цепи и во всей схеме, является комплексным и определяется по закону Ома: · ток через резистор · ток через конденсатор · ток через катушку · ток во всей схеме В том случае, если в схеме содержится только один элемент (резистор, конденсатор или катушка), ток во всей схеме будет равен току через этот элемент. Активная мощность в общем виде определяется по формуле:
где U, I – действующие значения напряжения и тока соответственно равные модулю их комплексов; cosφ – коэффициент мощности. Согласно приведенной выше формуле, активная мощность во всей цепи и на отдельных ее участках равна: · на катушке · на резисторе · на конденсаторе · во всей схеме Реактивная мощность: · на катушке · на резисторе · на конденсаторе · во всей схеме Полная мощность:
Активная составляющая тока в общем виде определяется по формуле:
Активная составляющая тока на отдельных участках цепи и в цепи, содержащей все три элемента, равна: · на резисторе · на конденсаторе · на катушке · во всей схеме Реактивная составляющая тока в общем виде:
Реактивная составляющая тока на отдельных участках цепи и в цепи, содержащей все три элемента, равна: · на резисторе · на конденсаторе · на катушке · во всей схеме Приведенные выше формулы для удобства вычислений сведены в табл. 2.3. Многоугольник проводимостей строится для цепей с параллельным соединением элементов. Он представляет собой изображение проводимостей элементов цепи с помощью векторов на комплексной плоскости (рис. 2.2).
Таблица 2.3
При построении векторной диаграммы задаются масштабами токов и напряжений, а при построении многоугольника проводимостей – масштабами проводимостей. Векторную диаграмму и многоугольник проводимостей можно строить, имея запись комплекса в показательной форме, т.е. по значениям модуля и фазы. При этом векторы длиной равной модулю комплексной величины откладываются из начала координат под углом к действительной оси равным фазе. Однако на практике удобнее проводить построения, используя алгебраическую форму записи, поскольку при этом вещественная и мнимая составляющие комплексной величины непосредственно откладываются на соответствующих осях комплексной плоскости, определяя положение точки на ней. Затем путем параллельного переноса векторы выстраиваются на комплексной плоскости согласно расположению элементов электрической цепи. Построение векторной диаграммы токов предполагает расчет комплексов токов в каждой ветви цепи с последующим суммированием векторов тока в узле схемы непосредственно на комплексной плоскости. Аналогично выполняется построение многоугольника проводимостей.
5. Контрольные вопросы
1. Какие вы знаете схемы замещения источников электрической энергии? 2. Законы Кирхгофа. 3. В чем заключается расчет электрических цепей? Назовите методы расчета? 4. Назовите основные величины, характеризующие синусоидальный ток. 5. Изобразите синусоидально изменяющуюся величину с помощью вектора на комплексной плоскости. 6. Дайте определение понятиям «комплексная амплитуда», «комплекс тока», «мгновенное значение тока». 7. Комплексная проводимость в алгебраической и показательной форме записи. 8. Что такое коэффициент мощности? Каким образом его можно повысить? 9. Какой прибор используется для измерения мощности? В чем особенности включения обмоток этого прибора в цепь? Какую мощность он измеряет? 10. Дайте определение понятиям «векторная диаграмма» и «топографическая диаграмма». Каковы особенности взаимного расположения на них векторов напряжения и тока для активных и реактивных элементов? Лабораторная работа №3
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 591; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.233.71 (0.01 с.) |

 .
.
 ;
;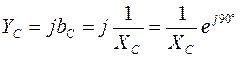 ,
, - емкостное сопротивление;
- емкостное сопротивление;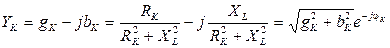 ,
, ;
; 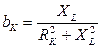 ;
;  ;
; - индуктивное сопротивление;
- индуктивное сопротивление;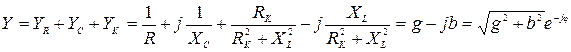 ,
, ;
;  ;
;  .
.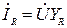 ;
; ;
;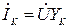 ;
; .
.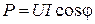 ,
, ;
; ;
; ;
; ;
; ;
; ;
; .
. .
. .
. ;
; ;
; ;
; .
. .
. ;
; ;
; ;
; .
.