c — опора с полным защемлением;
Содержание книги
- Проектирование, сопровождаемое испытаниями
- Таблица 3.1 — Прочностные и деформативные характеристики бетона
- Рисунок 3.1 — Номограммы для определения коэффициента ползучести j(¥, t0) для бетона
- при нормальных условиях окружающей среды
- Таблица 3.3 — Значения kh в формуле (3.9)
- Рисунок 3.2 — График зависимости «напряжение — относительная деформация»
- Рисунок 3.3 — Параболически-прямоугольная диаграмма для бетона при сжатии
- Рисунок 3.6 — Зависимость между напряжением и относительной деформацией
- при многоосном сжатии (бетон с ограничением поперечных деформаций)
- Характеристики пластичности (деформативности)
- Рисунок 3.7 — Диаграммы «напряжение — относительная деформация»
- Рисунок 3.8 — Идеализированная (А) и расчетная (В) диаграммы
- Рисунок 3.9 — Диаграмма «напряжение — относительная деформация»
- для типичной напрягаемой стали (абсолютные значения показывают
- Рисунок 3.10 — Идеализированная (А) и расчетная (В) диаграммы
- Анкерные устройства и зоны анкеровки
- Таблица 4.1 — Классы условий эксплуатации, соответствующие условиям окружающей среды согласно EN 206-1
- Коррозия, вызванная хлоридами. Окончание таблицы 4.1. Коррозия, вызванная хлоридами морской воды. Воздействие попеременного замораживания и оттаивания
- Таблица 4.2 — Минимальная толщина слоя cmin,b, требования к обеспечению сцепления бетона с арматурой
- Таблица 4.3N — Рекомендуемая классификация конструкций
- Допустимые отклонения при проектировании
- Специальные требования для фундаментов
- Случаи нагружения и сочетания воздействий
- Рисунок 5.1 — Примеры воздействия геометрических несовершенств
- Эффективная ширина полок (все предельные состояния)
- c — опора с полным защемлением;
- Линейно-упругий расчет с ограниченным перераспределением
- Пластический расчет балок, рам и плит
- Рисунок 5.5 — Угол пластического поворота qs для армированных поперечных сечений
- поперечных сечений железобетона для классов арматуры В и С.
- Расчет эффектов второго порядка при осевой нагрузке
- Упрощенный критерий для эффектов второго порядка
- Гибкость и расчетная длина для отдельных элементов
- Общий эффект второго порядка в зданиях
- Метод, основанный на номинальной жесткости
- Коэффициент увеличения момента
- Метод, основанный на номинальной кривизне
- Боковая (поперечная) неустойчивость гибких балок
- Предварительно напряженные элементы и конструкции
- Усилие предварительного напряжения во время напряжения
- Усилие предварительного напряжения
- Прямые (первые) потери усилия предварительного напряжения при предварительном натяжении
- Таблица 5.1 — Коэффициенты трения m для пост-натягиваемых напрягающих элементов, располагаемых в конструкции, и внешних напрягающих элементов без сцепления
- Потери от проскальзывания в анкерном устройстве
- Учет предварительного напряжения в расчете
- Влияние предварительного напряжения в предельном состоянии по эксплуатационной пригодности и предельном состоянии по усталости
- Предельные состояния по несущей способности (ULS)
- Рисунок 6.1 — Возможное распределение относительных деформаций
- Элементы, не требующие по расчету поперечной арматуры
- а — для балки с непосредственной опорой;
а — разрезные элементы;
b — неразрезные элементы;
c — опора с полным защемлением;
d — расположение опоры;
е — консоль
(2) Неразрезные плиты и балки должны рассчитываются, как правило, с учетом допущения, что опоры не ограничивают поворота.
(3) Если балка или плита монолитно соединены с опорами, как правило, необходимо определять критический опорный расчетный момент по грани опоры. Расчетный момент и реакции, передающиеся на опору (например, колонна, стена и т. п.), как правило, следует определять как наибольшие из значений, полученных из упругого расчета и расчета с учетом перераспределения усилий.
Примечание — Момент по грани опоры должен составлять не менее 0,65 момента при полной заделке конца элемента.
(4) Независимо от метода расчета в неразрезных балках или плитах, опоры которых могут быть рассмотрены как не препятствующие повороту (например, над стенами), расчетное значение момента над опорой, определенное при расчетном пролете, равном расстоянию между центрами опор, может быть уменьшено на значение DMEd:
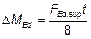 , (5.9) , (5.9)
где FEd,suр — расчетное значение опорной реакции;
t — глубина опоры (см. рисунок. 5.4 b).
Примечание — Если используются специальные опоры, то, как правило, для значения t выбирается ширина опоры.
5.4 Линейно-упругий расчет
(1) Линейный расчет элементов, основанный на положениях теории упругости, может быть использован для проверки как предельных состояний по эксплуатационной пригодности, так и по несущей способности.
(2) Для определения эффекта от воздействий может производиться линейный расчет при следующих предположениях:
i) поперечные сечения работают без трещин;
ii) соблюдается линейная зависимость между напряжениями и относительными деформациями;
iii) принимается среднее значение модуля упругости.
(3) Для эффектов, вызванных температурными деформациями, осадками и усадкой при проверке предельного состояния по несущей способности может быть принята уменьшенная жесткость сечений с трещинами, пренебрегая работой бетона на растяжение, но учитывая воздействие ползучести. При проверке предельных состояний по эксплуатационной пригодности следует, как правило, учитывать развитие трещин.
|