
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Боковая (поперечная) неустойчивость гибких балокСодержание книги
Поиск на нашем сайте
5.8.8.3 Кривизна (1) Для элементов с постоянными симметричными сечениями (включая арматуру) применяется следующая формула:
где Kr — корректирующий коэффициент, зависящий от продольной нагрузки, см. 5.8.8.3 (3); Кj — коэффициент, учитывающий влияние ползучести, см. 5.8.8.3 (4); здесь d — полезная высота, см. 5.8.8.3 (2). (2) Если вся арматура не сконцентрирована у противоположных сторон, а частично распределена параллельно плоскости изгиба, то d определяется по формуле
При этом is — радиус инерции площади всей арматуры. (3) Kr в формуле (5.34) следует принимать следующим образом:
где здесь NEd — расчетное значение продольного усилия; nbal — значение n при максимальном сопротивлении изгибу; допускается принимать равным 0,4;
где As — общая площадь сечения арматуры; Ас — общая площадь сечения бетона. (4) Влияние ползучести следует учитывать коэффициентом
где jef — эффективный коэффициент ползучести, см. 5.8.4;
l — гибкость, см. 5.8.3.1. 5.8.9 Двухосный изгиб (1) Общий метод, описанный в 5.8.6, может быть также использован для двухосного изгиба. Следующие правила действительны, когда применяются упрощенные методы. Особое внимание необходимо уделить нахождению сечения элемента с критической комбинацией моментов. (2) В качестве первого шага необходимо произвести раздельный расчет в направлениях обеих главных осей, без учета двухосного изгиба. Несовершенства необходимо учитывать только в направлении, в котором они больше всего приводят к самым неблагоприятным воздействиям. (3) Не требуется никакой дальнейшей проверки, если для гибкости выполняются следующие условия:
и если относительный эксцентриситет ey/h и ez/b (рисунок 5.8), удовлетворяет одному из условий:
где b, h — ширина и высота сечения;
здесь iy, iz — радиусы инерции соответственно относительно оси y и оси z; lу, lz — гибкость l0/i соответственно относительно оси y и оси z;
здесь MEdy — расчетное значение момента относительно оси y, включая моменты с учетом эффекта второго порядка; MEdz — расчетное значение момента относительно оси z, включая моменты с учетом эффекта второго порядка; NEd — расчетное значение продольного усилия для соответствующего сочетания нагрузок.
Рисунок 5.8 — Определение эксцентриситетовey и ez (4) Если не выполняются условия (5.38), то необходимо учитывать двухосный изгиб, включая влияние эффектов второго порядка в обоих направлениях (если ими нельзя пренебречь согласно 5.8.2 (6) или 5.8.3). При отсутствии более точного расчета сечений при двухосном изгибе может быть использован следующий упрощенный критерий:
где MEdz/y — расчетный момент относительно соответствующей оси, включая момент от эффектов второго порядка; MRdz/y — предельный момент в соответствующем направлении; a — показатель степени: для круглых и эллиптических сечений а = 2;
для прямоугольных сечений: NEd/NRd 0,1 0,7 1,0 a 1,0 1,5 2,0 для промежуточных значений допускается линейная интерполяция, здесь NEd — расчетное значение продольной силы; NRd = Acfcd + Asfyd — расчетное значение сопротивления сечения продольной силе, Ac — площадь брутто бетонного сечения; As — площадь продольной арматуры. (1)Р При определенных обстоятельствах необходимо учитывать боковую неустойчивость гибких балок, например, для сборных балок при транспортировке и монтаже, для балок без достаточного бокового раскрепления в готовой конструкции и т. д. Геометрические несовершенства должны быть учтены в расчете. (2) При расчете балок в нераскрепленных условиях боковое перемещение l/300 необходимо принять как геометрическое несовершенство, причем l — общая длина балки. В готовых конструкциях может быть учтено раскрепление присоединенными элементами. (3) Влияние эффектов второго порядка в отношении боковой неустойчивости может не учитываться, если будут выполнены следующие условия:
— для постоянных ситуаций — для переходных ситуаций где l0t — расстояние между раскреплениями от кручения; Н — общая высота балки в центральной части пролета l0t; В — ширина сжатой полки. (4) Кручение, связанное с боковой неустойчивостью, необходимо учитывать при расчете поддерживающей конструкции.
|
||||||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 5; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.92.6 (0.01 с.) |

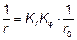 , (5.34)
, (5.34)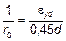 ,
,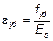 ;
;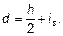 (5.35)
(5.35)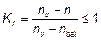 , (5.36)
, (5.36)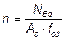 — относительное продольное усилие;
— относительное продольное усилие;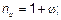
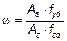 ,
,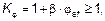 (5.37)
(5.37)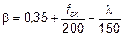 ;
;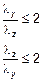 и (5.38а)
и (5.38а)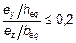 или
или 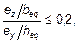 (5.38b)
(5.38b)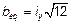 и
и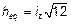 — для эквивалентного прямоугольного сечения,
— для эквивалентного прямоугольного сечения,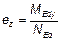 — эксцентриситет нагрузки в направлении оси z;
— эксцентриситет нагрузки в направлении оси z;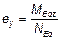 — эксцентриситет нагрузки в направлении оси у,
— эксцентриситет нагрузки в направлении оси у,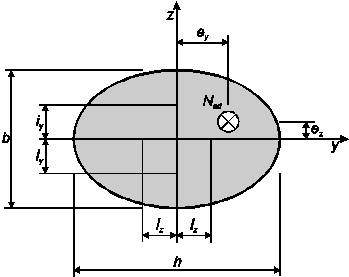
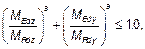 (5.39)
(5.39)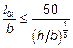 и h/b £ 2,5; (5.40а)
и h/b £ 2,5; (5.40а)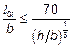 и h/b £ 3,5, (5.40b)
и h/b £ 3,5, (5.40b)


