
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод, основанный на номинальной жесткостиСодержание книги
Поиск на нашем сайте 5.8.4 Ползучесть (1)P При расчете с учетом эффектов второго порядка необходимо учитывать влияние ползучести, включая общие условия ползучести (см. 3.1.4), а также продолжительность действия различных нагрузок в рассматриваемых расчетных сочетаниях. (2) Продолжительность нагрузки в упрощенном варианте учитывается с помощью эффективного коэффициента ползучести jef, который при использовании совместно с расчетной нагрузкой дает ту деформацию ползучести (кривизну), которая соответствует практически постоянной нагрузке.
где M0Eqp — изгибающий момент с учетом эффекта первого порядка при практически постоянном сочетании нагрузок (предельное состояние по эксплуатационной пригодности); M0Ed — изгибающий момент с учетом эффекта первого порядка при расчетном сочетании нагрузок (предельное состояние по несущей способности). Примечание — Возможно определить значение jef по полным значениям изгибающих моментов M0Eqp (3) Если отношение M0Eqp/M0Ed изменяется в элементе или конструкции, то оно может быть рассчитано для поперечного сечения с максимальным моментом или может быть применено репрезентативное среднее значение. (4) Влияние ползучести не учитывается, т. е. jef = 0, если выполнены три следующих условия: j(¥,t0) £ 2; l £ 75;
При этом M0Ed является моментом, определенным с учетом эффекта первого порядка, а h — высотой поперечного сечения в соответствующем направлении. Примечание — Если условия согласно 5.8.2 (6) или 5.8.3.3 будут выполнены только частично, то следует учитывать эффекты второго порядка и ползучесть, кроме случаев, когда механический коэффициент армирования (w, см. 5.8.3.1 (1)) составляет не менее 0,25. 5.8.5 Методы расчета (1) Методы расчета включают общий метод, основанный на нелинейном расчете с учетом эффектов второго порядка (см. 5.8.6) и следующих двух упрощенных методов. (а) Метод, основанный на номинальной жесткости, см. 5.8.7. (b) Метод, основанный на номинальной кривизне, см. 5.8.8. Примечание 1 — Выбор упрощенного метода ((a) и (b)) для применения в своей стране может быть указан Примечание 2 — Номинальные моменты, определенные с учетом эффектов второго порядка с помощью упрощенных методов (a) и (b) иногда могут быть больше, чем соответствующие потере устойчивости. Тем самым необходимо убедиться, что общий момент совместим с сопротивлением поперечного сечения. (2) Метод (a) может применяться как для отдельных элементов, так и для конструкции в целом, если значения номинальной жесткости рассчитаны предварительно, см. 5.8.7. (3) Метод (b) подходит преимущественно для отдельных элементов, см. 5.8.8. При реальных предпосылках в части распределения кривизны метод по 5.8.8 может быть применен для конструкций. 5.8.6 Общий метод (1)P Общий метод основан на нелинейном расчете, включающем геометрическую нелинейность, т. е. эффекты второго порядка. Применяются общие правила для нелинейного расчета по 5.7. (2)Р Следует использовать зависимости напряжений от относительных деформаций для бетона и стали, пригодные для общего расчета. Необходимо учитывать влияние ползучести. (3) Могут быть использованы зависимости «напряжение — относительная деформация» для бетона и стали, которые приведены в 3.1.5, уравнении (3.14) и 3.2.7 (см. рисунок 3.8). По определенным на основе
Примечание — Значение gСE может быть приведено в национальном приложении. Рекомендуемое значение равно 1,2. (4) При отсутствии более точных моделей ползучесть может быть учтена умножением всех значений относительных деформаций диаграммы «напряжение — относительная деформация» для бетона согласно 5.8.6 (3) на коэффициент (1 + jef), где jef является эффективным коэффициентом ползучести согласно 5.8.4. (5) Может быть учтен благоприятный эффект ужесточения при растяжении. Примечание — Этот эффект является благоприятным и для упрощения расчетов в каждом случае может (6) Обычно условия равновесия и совместности деформаций проверяются в нескольких поперечных сечениях. Упрощенной альтернативой является рассмотрение только критических сечений
|
||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 11; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.72.78 (0.008 с.) |

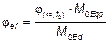 , (5.19)
, (5.19)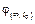 — предельная характеристика ползучести по 3.1.4;
— предельная характеристика ползучести по 3.1.4;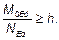
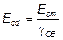 . (5.20)
. (5.20)


