Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
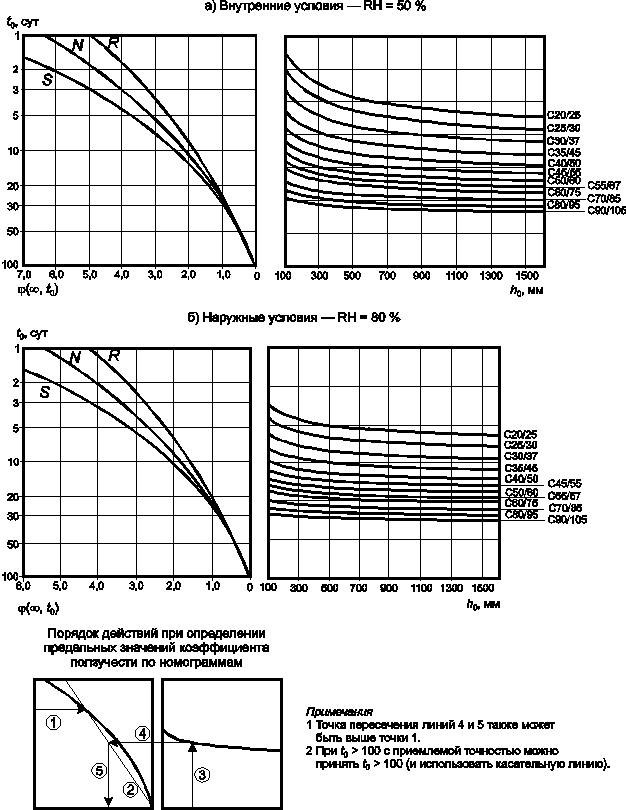
Рисунок 3.1 — Номограммы для определения коэффициента ползучести j(¥, t0) для бетонаСодержание книги
Поиск на нашем сайте
3.1.3 Упругие деформации (1) Упругие деформации бетона существенно зависят от его состава (особенно от заполнителей). Значения, приведенные в настоящем техническом кодексе, должны рассматриваться как ориентировочные для общего применения. Однако они должны быть специально оценены, если конструкция чувствительно реагирует на отклонения от приведенных в стандарте общих значений. (2) Модуль упругости бетона зависит от модулей упругости его составляющих. Приближенные значения модуля упругости Ecm, определенные для секущей, проведенной через точки sс = 0 и 0,4fcm для бетона на кварцевых заполнителях, приведены в таблице 3.1. При заполнителях из известняка или песчаника эти значения должны быть уменьшены соответственно на 10 % и 30 %. При базальтовых заполнителях значение должно быть увеличено на 20 %. Примечание — Национальное приложение может содержать не противоречащую дополняющую информацию. (3) Изменение модуля упругости во времени может быть оценено при использовании зависимости
где Eсm(t) и fcm(t) — соответственно значения модуля упругости и средней прочности в возрасте t сут; Ecm и fcm — значения модуля упругости и средней прочности в возрасте 28 сут. Взаимосвязь между fcm(t) и fcm представлена выражением (3.1). (4) Коэффициент Пуассона может быть принят равным 0,2 для бетона без трещин и 0 — для бетона с трещинами. (5) Если более точная информация отсутствует, линейный коэффициент температурного расширения принимается равным 10 · 10–6 · К–1 . 3.1.4 Ползучесть и усадка (1)P Ползучесть и усадка бетона зависят, в основном, от относительной влажности окружающей среды, геометрических размеров конструктивного элемента и состава бетона. На ползучесть бетона также оказывает влияние степень зрелости бетона (начальная прочность) при первоначальном приложении нагрузки, а также продолжительность нагружения и величина нагрузки. (2) Коэффициент ползучести j(t, t0) связан с касательным модулем упругости Еc, который может быть принят равным 1,05Еcm. Если особая точность не требуется, то в качестве предельной характеристики ползучести j(∞, t0) может быть принято значение, приведенное на рисунке 3.1, при условии, что бетон в момент времени, соответствующий приложению нагрузки, t = t0, не подвергается сжимающим напряжениям, большим, чем 0,45fck(t0). Примечание — Другая информация, включая развитие ползучести во времени, приведена в приложении В. (3) Деформация ползучести бетона eсс(¥, t0) в возрасте t = ∞, при постоянном напряжении сжатия sс, приложенном во время t = t0, рассчитывается по формуле ecc (4) Если напряжения сжатия бетона в возрасте t0 превышает значение 0,45fck(t0),то, как правило, следует учитывать нелинейную ползучесть. Такой высокий уровень напряжений может появиться
При этом
ks — отношение «напряжение — прочность» sс/fck(t0), где sc — напряжение сжатия, а fck(t0) — характеристическая прочность бетона в момент времени, соответствующий нагружению. (5) Значения, приведенные на рисунке 3.1, действительны при температуре окружающей среды j(¥, t0) — предельное значение коэффициента ползучести; t0 — возраст бетона в момент нагружения, в сутках; h0 — приведенный размер, равный 2Aс/u, где Ac — площадь поперечного сечения бетона; S — класс S по 3.1.2 (6); N — класс N по 3.1.2 (6); R — класс R по 3.1.2 (6).
|
||||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 58; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

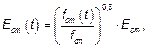 (3.5)
(3.5)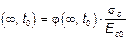 . (3.6)
. (3.6)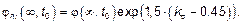
 (3.7)
(3.7)
 jnl(¥, t0) — нелинейный условный коэффициент ползучести, вводимый взамен j(¥, t0);
jnl(¥, t0) — нелинейный условный коэффициент ползучести, вводимый взамен j(¥, t0);