
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическая модель работы нейронной сети. Теоремы Колмогорова и Хехт-Нильсона. Основные типы нейронных сетей.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Искусственные нейронные сети (ИНС) — математические модели, а также их программные или аппаратные реализации, построенные по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма.
Нейронные сети не программируются в привычном смысле этого слова, они обучаются (и в этом их преимущество). Технически обучение заключается в нахождении коэффициентов связей между нейронами. В процессе обучения нейронная сеть способна выявлять сложные зависимости между входными данными и выходными, а также выполнять обобщение. Это значит, что в случае успешного обучения сеть сможет вернуть верный результат на основании данных, которые отсутствовали в обучающей выборке, а также неполных и/или «зашумленных», частично искаженных данных. Устройство модели. Пусть имеется n входных величин x1,…,xn бинарных признаков, описывающих объект x. Значения этих признаков будем трактовать как величины импульсов, поступающих на вход нейрона через n входных синапсов (связей). Будем считать, что, попадая в нейрон, импульсы складываются с весами ω1,…,ωn. Если вес положительный, то соответствующий синапс возбуждающий, если отрицательный, то тормозящий. Если суммарный импульс превышает заданный порог активации ω0, то нейрон возбуждается и выдаёт на выходе 1, иначе выдаётся 0. Таким образом, нейрон вычисляет n-арную булеву функцию Теорема Колмогорова: Академикам А.Н. Колмогорову и В.И. Арнольду удалось доказать, что любая непрерывная функция n переменных f(x1, x2,... xn) всегда может быть представлена в виде суммы непрерывных функций одного переменного f1(x1) + f2(x1) +... + fn(xn). Теорема Хехт-Нильсона: В 1987–1991 гг. профессором Калифорнийского университета (США) Р.Хехт-Нильсеном теоремы Арнольда – Колмогорова были переработаны применительно к нейронным сетям. Было доказано, что для любого множества непротиворечивых между собой пар произвольной размерности (Xq, Dq), q = 1,..., Q, существует двухслойный персептрон с сигмоидными активационными функциями и с конечным числом нейронов, который для каждого входного вектора Xq формирует соответствующий ему выходной вектор Dq. Таким образом, была доказана принципиальная возможность построения нейронной сети, выполняющей преобразование, заданное любым множеством различающихся между собой обучающих примеров, и установлено, что такой универсальной нейронной сетью является двухслойный персептрон, т.е. персептрон с одним скрытым слоем, причем активационные функции его нейронов должны быть сигмоидными. (s = 1 / (1+exp(-x)) – сигмоида) Этапы решения задач: - 1) Сбор данных для обучения является самым сложным этапом решения задачи. Исходные данные (обучающие пары/векторы) преобразуются к виду, в котором их можно подать на входы сети. Обучение сети на «сыром» наборе, как правило, не даёт качественных результатов. Существует ряд способов улучшить «восприятие» сети (например, Нормировка - выполняется, когда на различные входы подаются данные разной размерности. Например, на первый вход сети подаются величины со значениями от нуля до единицы, а на второй — от ста до тысячи. При нормировке размерности всех входных и выходных данных сводятся воедино). 2) Выбор топологии сети - Выбирать тип сети следует исходя из постановки задачи и имеющихся данных для обучения. Для обучения с учителем требуется наличие для каждого элемента выборки «экспертной» оценки. Иногда получение такой оценки для большого массива данных просто невозможно. В этих случаях естественным выбором является сеть, обучающаяся без учителя, например, самоорганизующаяся карта Кохонена или нейронная сеть Хопфилда. При решении других задач, таких как прогнозирование временных рядов, экспертная оценка уже содержится в исходных данных и может быть выделена при их обработке. В этом случае можно использовать многослойный перцептрон или сеть Ворда; 3) Экспериментальный подбор характеристик сети - Для сетей, подобных перцептрону, это будет число слоев, число блоков в скрытых слоях (для сетей Ворда), наличие или отсутствие обходных соединений, передаточные функции нейронов. При выборе количества слоев и нейронов в них следует исходить из того, что способности сети к обобщению тем выше, чем больше суммарное число связей между нейронами. С другой стороны, число связей ограничено сверху количеством записей в обучающих данных; 4) Экспериментальный подбор параметров обучения - От правильного выбора параметров зависит не только то, насколько быстро ответы сети будут сходиться к правильным ответам. Например, выбор низкой скорости обучения увеличит время схождения, однако иногда позволяет избежать паралича сети; 5) Собственно обучение - В процессе обучения сеть в определенном порядке просматривает обучающую выборку. Порядок просмотра может быть последовательным, случайным и т. д., при этом один полный проход по выборке называется эпохой обучения. - Обучение с учителем — выходное пространство решений нейронной сети известно; - Обучение без учителя — нейронная сеть формирует выходное пространство решений только на основе входных воздействий. При обучении с учителем набор исходных данных делят на две части — собственно обучающую выборку и тестовые данные. Обучающие данные подаются сети для обучения, а проверочные используются для расчета ошибки сети (проверочные данные никогда для обучения сети не применяются). Таким образом, если на проверочных данных ошибка уменьшается, то сеть действительно выполняет обобщение. Если ошибка на обучающих данных продолжает уменьшаться, а ошибка на тестовых данных увеличивается, значит, сеть перестала выполнять обобщение и просто «запоминает» обучающие данные. Это явление называется переобучением сети. В таких случаях обучение обычно прекращают; 6) Проверка адекватности обучения - Даже в случае успешного, на первый взгляд, обучения сеть не всегда обучается именно тому, чего от неё хотел создатель. Тестирование качества обучения нейросети необходимо проводить на примерах, которые не участвовали в ее обучении. При этом число тестовых примеров должно быть тем больше, чем выше качество обучения; 7) Корректировка параметров, окончательное обучение; 8) Вербализация сети с целью дальнейшего использования. Известные применения: Распознавание образов и классификация; Принятие решений и управление; Кластеризация; Прогнозирование. Известные типы сетей: § Перцептрон - математическая и компьютерная модель восприятия информации мозгом (кибернетическая модель мозга), предложенная Фрэнком Розенблаттом. Основная математическая задача, с которой он справляется, — это линейное разделение любых нелинейных множеств; § Многослойный перцептрон - перцептрон с дополнительными слоями А-элементов (скрытый внутренний слой), расположенными между S-(входы) и R-(выходы) элементами; § Сеть Ворда - искусственная нейронная сеть, топология которой характеризуется тем, что внутренние (скрытые) слои нейронов разбиты на блоки (решение задач прогнозирования и распознавания образов); § Сеть Кóхонена - класс нейронных сетей, основным элементом которых является слой Кохонена – он состоит из адаптивных линейных сумматоров («линейных формальных нейронов»). Как правило, выходные сигналы слоя Кохонена обрабатываются по правилу «победитель забирает всё»: наибольший сигнал превращается в единичный, остальные обращаются в ноль.; § Сеть Джордана (рекуррентная) - вид нейронных сетей, который получается из многослойного перцептрона, если на его вход подать, помимо входного вектора, выходной с задержкой на один или несколько тактов; § Сеть Элмана (рекуррентная) - один из видов рекуррентной сети, которая так же как и сеть Джордана получается из многослойного перцептрона введением обратных связей, только связи идут не от выхода сети, а от выходов внутренних нейронов. Это позволяет учесть предысторию наблюдаемых процессов и накопить информацию для выработки правильной стратегии управления. Эти сети могут применяться в системах управления движущимися объектами, так как их главной особенностью является запоминание последовательностей; § Когнитрон - искусственная нейронная сеть на основе принципа самоорганизации. Своей архитектурой когнитрон похож на строение зрительной коры, имеет иерархическую многослойную организацию, в которой нейроны между слоями связаны только локально. Обучается без учителя. Каждый слой мозга реализует различные уровни обобщения; входной слой чувствителен к простым образам, таким, как линии, и их ориентации в определенных областях визуальной области, в то время как реакция других слоев является более сложной, абстрактной и независимой от позиции образа; § Неокогнитрон - является дальнейшим развитием идеи когнитрона и более точно отражает строение зрительной системы, позволяет распознавать образы независимо от их преобразований, вращений, искажений и изменений масштаба. Неокогнитрон может как самообучаться, так и обучаться с учителем. Неокогнитрон получает на входе двумерные образы, аналогичные изображениям на сетчатке глаза, и обрабатывает их в последующих слоях аналогично тому, как это было обнаружено в зрительной коре человека; § Осцилляторная нейронная сеть - нейронные сети, основными структурными единицами которых являются осцилляторы. Функционируют ОНС за счет колебаний отдельных элементов или групп элементов и их взаимодействия; § Сеть радиальных базисных функций (RBF-сеть) - нейронная сеть прямого распространения сигнала, которая содержит промежуточный (скрытый) слой радиально симметричных нейронов. Такой нейрон преобразовывает расстояние от данного входного вектора до соответствующего ему "центра" по некоторому нелинейному закону (обычно функция Гаусса); § Вероятностная сеть – сеть, которая фактически учится оценивать функцию плотности вероятности. В задачах классификации выходы сети можно с пользой интерпретировать как оценки вероятности того, что элемент принадлежит некоторому классу; § Сеть обобщенной регрессии - устроена аналогично вероятностной нейронной сети (ВНС), но она предназначена для решения задач регрессии, а не классификации.
|
||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 548; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.140.152 (0.01 с.) |

 ИНС представляют собой систему соединённых и взаимодействующих между собой простых процессоров (искусственных нейронов). Каждый процессор подобной сети имеет дело только с сигналами, которые он периодически получает, и сигналами, которые он периодически посылает другим процессорам.
ИНС представляют собой систему соединённых и взаимодействующих между собой простых процессоров (искусственных нейронов). Каждый процессор подобной сети имеет дело только с сигналами, которые он периодически получает, и сигналами, которые он периодически посылает другим процессорам.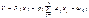 В теории нейронных сетей функцию φ, преобразующую значение суммарного импульса в выходное значение нейрона, принято называть функцией активации.
В теории нейронных сетей функцию φ, преобразующую значение суммарного импульса в выходное значение нейрона, принято называть функцией активации.


