Эффективность аппроксимации с помощью нейронных сетей и систем нечеткого вывода.

Эффективность аппарата нейросетей определяется их аппроксимирующей способностью, причем НС являются универсальными функциональными аппроксиматорами. С помощью НС можно выразить любую непрерывную функциональную зависимость на основе обучения НС, без предварительной аналитической работы по выявлению правил зависимости выхода от входа.

Недостатком нейросетей является невозможность объяснить выходной результат, так как значения распределены по нейронам в виде значений коэффициентов весов. Основной трудностью в применении нечётких экспертных систем служит необходимость явно сформулировать правила проблемной области в форме продукции. В нечётких экспертных системах легко построить объяснение результата в форме протокола рассуждений. Поэтому в настоящее время создаются гибридные технологии, сочетающие преимущества нечётких систем и нейронных сетей.

Свойство универсальности применения систем нечёткого вывода доказано рядом следующих фундаментальных теорем.

В 1992 г. У. Ванг показал, что справедливо утверждение: если нечёткая импликация основана на операции min, функция принадлежности задаётся гауссовым распределением

И используется центральный метод дефазификации, то система нечёткого вывода является универсальным аппроксиматором.

В 1995 г. К. Кастро доказал справедливость следующей теоремы: если импликация основана на использовании произведения по Ларсену, а функции принадлежности треугольные, то при использовании центроидной дефазификации нечёткий контроллер является универсальным аппроксиматором.

Линейно-сепарабельные задачи.

Обучить – значит провести разделяющую образцы прямую, найти ее направление.

Признаки объекта интерпретируются как координаты признакового пространства, тогда каждый объект обучающей выборки представлен точкой пространства. Разграничительная поверхность определяется текущим состоянием весов. В состоянии до обучения такая поверхность не разделяет классы, а после обучения должна разделять.

Если разделяющая поверхность является n-мерной гиперплоскостью, то задача называется линейно сепарабельной.

X2

X1

O

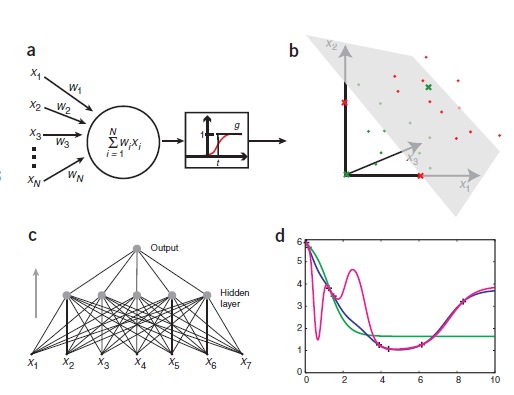
Рисунок 5Иллюстрация разбиения объектов на два класса

ИНС (искусственные НС) могут быть созданы путем имитации модели сетей нейронов на компьютере. Используя алгоритмы, которые имитируют процессы реальных нейронов, мы можем заставить сеть «учиться», что помогает решить множество различных проблем.

Модель нейрона представляется как пороговая величина (она проиллюстрирована на рисунке 1а). Модель получает данные от ряда других внешних источников, определяет значение каждого входа и добавляет эти значения. Если общий вход выше пороговой величины, то выход блока равен единице, в противном случае – нулю. Таким образом, выход изменяется от 0 до 1, когда общая «взвешенная» сумма входов равна пороговой величине. Точки в исходном пространстве, удовлетворяющие этому условию, определяют, так называемые, гиперплоскости. В двух измерениях, гиперплоскость – линия, в то время как в трех измерениях, гиперплоскость является нормальной (перпендикулярной) плоскостью. Точки с одной стороны от гиперплоскости классифицируются как 0, а точки с другой стороны – 1. Это означает, что задача классификации может быть решена с использованием пороговой величины, если два класса будут разделены гиперплоскостью. Эти проблемы называются линейно сепарабельными и изображены на рисунке 1b.

Нейронная сеть как универсальный аппроксиматор.

См. вопрос 10

Сети Кохонена. Алгоритм обучения «победитель забирает все»

Сети Кохонена

Нейронные сети Кохонена — класс нейронных сетей, основным элементом которых является слой Кохонена. Слой Кохонена состоит из адаптивных линейных сумматоров («линейных формальных нейронов»). Как правило, выходные сигналы слоя Кохонена обрабатываются по правилу «победитель забирает всё»: наибольший сигнал превращается в единичный, остальные обращаются в нуль.

По способам настройки входных весов сумматоров и по решаемым задачам различают много разновидностей сетей Кохонена:

· Сети векторного квантования сигналов, тесно связанные с простейшим базовым алгоритмом кластерного анализа (метод динамических ядер или K-средних)

· Самоорганизующиеся карты

· Сети векторного квантования, обучаемые с учителем

· Самоорганизующиеся карты решают задачу классификации. У нее есть сколько-то центров и после обучения к каждому этому центру она будет относить объекты по принципу ближайшего соседства. Обучается алгоритмом без учителя.