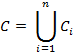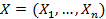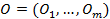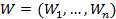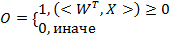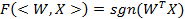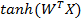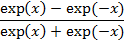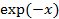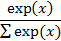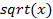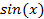ИС осуществляет логический вывод по базе нечетких правил по этапам.

1. Фазификация фактических данных, т.е. точное значение x₀ интерпретируется как нечеткая точка.

2. Композиция входной переменной и условной части правила: х₀ ° Ai, y₀ ° Bi, т. е. вычисляется уровень пригодности правила к ситуации. Если факт задан нечеткой точкой, то композиция сводится к выявлению соответствующей степени принадлежности.

3. Вычисление нечеткой импликации:

(х₀ ° Ai) ^ (y₀ ° Bi) → С_i для любого R.

Результатом выполнения п. 2 и 3 для всех правил являются N нечетких значений для выхода Z.

4. Агрегация среднего значения:

т.е. построение нечеткого значения выхода по результатам предыдущих этапов.

5. Дефазификация, т. е. выбор представляющего элемента но агрегированному нечеткому понятию.

Схемы нечеткого вывод у разных авторов уточняются до оператора нечеткой импликации. Распространены 5 схем нечеткого вывода:

1. По Мамдани: импликация моделируется минимумом, агрегация – максимумом
2. По Цукамото: для монотонных функций принадлежности. L₁', L₂' – уровни достоверности применения правил; z₁,z₂ – значения выходной переменной по первому и второму правилу:

z₁ = C₁^-1(L₁), z₂ =C₂^-1(L₂)

z = (L₁'* z₁ +L₂'* z₂)/(L₁'+ L₂')

Ввиду монотонности функций вычисления выходной переменной сводят к усреднению значений, полученных по разным правилам.

1. По Суджено: правые части правил вывода ограничиваются линейным случаем

Если х – А₁ и у – В₁, тогда z = a₁x + b₁y

1. По Ларсену: импликация выполняется с помощью произведения.
2. Упрощенная схема: Если х – А_i и у – В_i, тогда z = Z_i, где z – четкое значение.

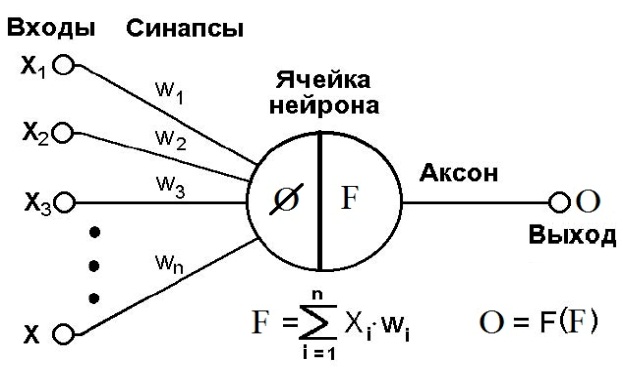
Поскольку правые части правил в упрощенной схеме задаются четко, то в результате вывода получается дискретное множество решений для каждого элемента, у которого задана определенная степень уверенности. В качестве выходной переменной выбирается значение с максимальной уверенностью.

Архитектура нечёткой экспертной системы

См. вопрос 3

Искусственная нейронная сеть. Математическая модель нейрона.

Искусственные нейронные сети представляют собой простейшие математические модели мозга. Понять основные принципы построения НС можно, рассматривая их как совокупность (сеть) отдельных структур (нейронов).

Биологический нейрон характеризуется наличием тела, входов, выходов и места их соединения:

1. Сома – тело,

2. Дендриты – дерево входов.

3. Аксоны – дерево выходов.

4. Синапсы – место соединения дендритов и аксонов. Синапсы имеют переменное сопротивление для переходных сигналов.

Принятые синапсами сигналы либо возбуждают нейрон, либо его тормозят в зависимости от порогового значения. Когда суммарное возбуждение достигает некоторого порога, нейрон возбуждается и посылает по аксону сигнал другим нейронам. Каждый синапс обладает уникальной синаптической силой, которая пропорционально своему значению изменяет передаваемый на нейрон входной сигнал. Дендрит имеет собственный приоритет, который он меняет в течение жизни.

Рисунок 2 Искусственный нейрон

Схема будущего элемента – взвешенный пороговый сумматор.

Биологический нейрон является взвешенным пороговым сумматором.

Математически нейрон характеризуется следующими параметрами:

1. Вектор входов

2. Вектор выходов

3. Вектор весов

4. Порог срабатывания ø

5. Функция активации F

Наиболее часто используемые функции активации

Название функции	Формула
Линейная
Функция «знак»
Униполярная сигмоидальная
Биполярная сигмоида
Гиперболический тангенс

Функция активации. Виды нейронных сетей.

Функция активации.

Особенности структуры НС составляют:

1. вид связей,

2. функции активации,

3. постсинаптические элементы:

· Линейный элемент вычисляет взвешенную сумму входов, что эквивалентно скалярному произведению векторов входов и весов, и сравнивает результат с порогом. Линейные ПСЭ раз­деляют пространство образцов с помощью пересекающихся гиперплоскостей.

· Нелинейный элемент;

· Радиальный элемент вычисляют квадрат расстояния между 2 точками пространства, представляющими вектор весов и входов. Радиальные ПСЭ эквивалентны гиперсферам в про­странстве образцов.

· Элемент деления специально разработаны исключительно для сетей регрессии. Сегодня многослойный перцептрон (МП) — это самая популярная архитектура, которая имеет ли­нейные ПСЭ и нелинейные ФА.

Функция активации	Формула функции активации	Комментарий
Линейная		Сигнал проходит без преоб­разования непосредственно на выход
Логистическая		S-образная кривая с выходом в диапазоне [0,1]
Гиперболическая		Гиперболический тангенс (tank): кривая, подобная логистической функции, но с диапазоном [-1, +1]
Экспонента		Гауссовская колоколообразная кривая
Мягкий максимум		Нормализованная экспонен­циальная функция
Квадратный корень		Используется для преобразо­вания квадрата расстояния в сетях Кохонена в расстояние на выходе
Синус		Используется вместе с РБФ
Кусочно-линейная	Нет	Кусочно-линейная аппрок­симация сигмоиды
Пороговая	Нет	Выход 1,0 или 0,0 в зависимости от результата

Виды нейронных сетей.

Классификация нейронных сетей связана с характером передачи сигнала, т.е. с наличием или отсутствием обратных связей. Среди нейронных сетей разделяют сети с прямым распределением сигнала и сети с обратными связями.

1. Сети прямого распространения сигнала называют слоистыми сетями или персептронами (от англ. perception – восприятие).

Персептроновым слоем называют не совокупность нейронов, а совокупность связей одного уровня.

Перцептрон – математическая модель фрагмента нейронной системы головного мозга, осуществляющего восприятие внешнего объекта. Первые перцептроны создавались как модель искусственного глаза. В настоящее время перцептрон представляет собой многослойную нейронную сеть прямого распространения сигнала, способную к обучению.

2. Сети с обратными связями или сети прямого и обратного распространения сигнала. Для сетей с обратными связями моделирование прохождения сигнала осложняется тем, что необходимо учитывать возврат сигнала. Обычно такое моделирование требует введение внутреннего времени (внутренних тактов срабатывания).

Виды нейронных сетей

НС без обратных связей

· многослойные перцептроны;

· сети Кохонена;

· нейронные сети с радиальными базисными функциями;

· байесовские сети регрессии;

· байесовские вероятностные НС;

· линейные многослойные перцептроны.

Полносвязные сети

Многослойный перцептрон – самая известная и очень старая архитектура, в которой идут подряд несколько слоев нейронов — входной, один или несколько скрытых слоев, и выходной слой. Почти всегда обучается методом обратного распространения ошибки — что автоматически означает, что мы должны предоставить для обучения набор пар «входной вектор — правильный выход».

Сеть такого типа обычно очень хорошо справляется с задачами, где:

1. ответ зависит только от того, что мы даем на вход сети, и никак не зависит от истории входов.

2. ответ не зависит/слабо зависит от высоких степеней и/или произведений параметров — функции этого типа сеть строить почти не умеет.

3. в наличии есть достаточно много примеров.

Сильные стороны — изучена со всех сторон, хорошо работает на своих задачах, если на некоторой задаче не работает (действительно не работает, а не по криворукости, как это бывает чаще всего) — то это повод утверждать, что задача сложнее, чем казалось.

Слабые стороны — неумение работать с динамическими процессами, необходимость большой обучающей выборки.

Перспективы — никаких существенных. Большинство серьезных задач, которые все еще требуют решения, не входят в класс задач, решаемых многослойным перцептроном c методом обратного распространения ошибки.

Радиальная базисная нейронная сеть (РБНС) состоит из двух слоев:

1. скрытого радиального базисного слоя из S¹ нейронов

2. выходного линейного слоя из S² нейронов.

Элементы первого слоя РБНС вычисляют расстояния между входным вектором и векторами весов первого слоя, сформированных из строк матрицы W^2,1. Вектор порогов B и расстояния поэлементно умножаются. Выход первого слоя можно выразить формулой:

Нейронные сети регрессии (НСР) имеют такой же, как и РБНС первый слой, но второй слой строится специальным образом. Для аппроксимации функций часто используются обобщенные сети регрессии.

1. Скрытый радиальный базисный слой из S¹ нейронов

2. Второй слой как и в случае РБНС выполняет поэлементное произведение строки W_1,2 и вектора выхода первого слоя a¹.

Целевое значение – это значение аппроксимируемой функции в обучающей выборке.

Вероятностные нейронные сети (ВНС) используются для решения проблемы классификации:

1. Слой радиальных базисных нейронов, который вычисляет расстояние и вектор индикаторов принадлежности другим входным векторам, используемым при обучении.

2. Слой суммирует эти значения для каждого класса входов и формирует выходы сети, как вектор вероятностей. Далее ФА определяет максимум вероятностей на выходе 2 слоя и устанавливает данный выход в 1, а остальные выходы в 0.

Сеть классифицирует входные вектора, назначая входу единственный класс на основе максимальной вероятности принадлежности.