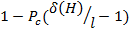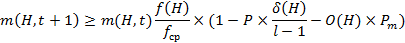Генетический алгоритм в псевдокоде.

Начало

Создать начальную популяцию

Оценить приспособленность каждой особи

Остановка = ложь

Пока не остановка выполнять

Начало

Повторить (размер популяции/2) раз

Начало

Выбрать 2 особи с высокой приспособленностью для скрещивания

Скрестить потомков

Оценить приспособленность потомков

Поместить потомков в новое поколение

Конец

Если приспособленность лучшего потомка > порога, то остановка = истина

Конец

Конец.

Кодировка хромосом. Оператор отбора.

Обычно хромосома представляется битовой строкой – 1 бит на 1 признак. Каждая хромосома состоит из генов (Пр. 1001101011 – хромосома).

Ген – каждая цифра.

Локус – отдельные позиции хромосомы, в которых располагаются гены.

Аллель – значение гена.

Функция приспособленности – ей может быть целевая функция оптимизации.

Генотип – структура хромосомы (относится к полной генетической модели)

Фенотип – вектор в пространстве параметров (относится к внешним наблюдаемым признакам)

Обычно, методика кодирования реальной переменной x состоит в ее преобразовании в двоичные целочисленные строки заданной длины.

Оператор селекции.

Селекция – отбор хромосом пропорционален величине их fitness функции.

Простейший способ пропорционального отбора – рулетка, который выбирает особей с помощью n запусков. Колесо рулетки содержит сектора для каждого члена популяции. Размер i -ого сектора пропорционален соответствующей величине P_s (i). При таком отборе члены популяции с более высокой приспособленностью выбираются чаще, чем особи с низкой. В настоящее время используют разные операторы отбора. Например, турнирный отбор реализует n турниров, чтобы выбрать n особей. Каждый турнир построен на выборке k элементов из популяции, и выбора лучшей особи среди них. Наиболее распространен турнирный отбор с k = 2. Элитные методы отбора гарантируют, что при отборе обязательно будут выживать лучшие члены популяции.

Рассмотрим пример кодирования хромосомы.

Пусть, известно, что для переменой x достаточно 8 разрядов. Установить соответствие между генотипом и фенотипом закодированных особей можно с помощью деления соответствующего двоичного целого числа на 2⁸-1. Например, 00000000 соответствует 0/255 или 0, тогда как 11111111 соответствует 255/255 или 1. Структура хромосомы для примера – 8-битовая строка. Генотип – это точка в 8-мерном хеммининговом пространстве, а фенотип – точка на прямой.

Сначала, пропорциональный отбор назначает каждой i -ой хромосоме вероятность P_s (i), равную отношению ее приспособленности к суммарной приспособленности популяции:

 

Площадь i-того символа пропорционален равной величине (отношение приспособленности i-той особи к суммарной приспособленности популяции). При таком отборе особи с более высокой функцией приспособленности выбираются чаще, чем с низкой.

Операторы рекомбинации и мутации.

Оператор скрещивания (оператор кроссовера)

Оператор скрещивания (кроссовера) позволяет по заданной маске делать из двух строк одну. Существует одноточечный, двухточечный и многоточечный кроссовер.

Пример одноточечного кроссовера.
Исходная строка	Маска	Результат

Одноточечный кроссовер работает следующим образом. Сначала, случайным образом выбирается одна из l - 1 точек разрыва. Точка разрыва – граница между соседними битами в строке. Родительские структуры разрываются в этой точке на два сегмента. Затем, соответствующие сегменты различных родителей склеиваются и получаются два генотипа потомков.

В двухточечном кроссовере выбираются две точки разрыва, и родительские хромосомы обмениваются сегментом, который находится между двумя этими точками.

В равномерном кроссовере, каждый бит первого родителя наследуется первым потомком с заданной вероятностью; в противном случае этот бит передается второму потомку.

После стадии кроссовера выполняются операторы мутации, которые с вероятностью P_m изменяют случайный бит в каждой строке на противоположный.

Оператор мутации

Оператор мутации с определённой вероятностью заменяет случайный бит на противоположный. Вероятность мутации намного меньше, чем вероятность кроссовера.

Сходимость ГА.

Схема хромосомы – это строка длины l (длина любой строки популяции), состоящая из знаков алфавита {0; 1; *}, где знак * обозначает неопределенный символ.

Порядок схемы – число определенных битов («0» или «1»).

Длина схемы – расстояние между крайними определенными битами в схеме .

Строящими блоками называют схемы, обладающие высокой приспособленностью, низким порядком и короткой длиной.

Сходимость алгоритма заключается в том, что он сходится к глобальному оптимуму. Стандартный ГА сходится. Дж. Голланд (1992) показал, что, если ГА явным образом обрабатывает n строк в каждом поколении, то он неявно обрабатывает порядка n³ коротких схем низкого порядка и с высокой приспособленностью. Это явление называется неявным параллелизмом. ГА экспоненциально увеличивает число примеров полезных схем или строящих блоков. Данное утверждение известно как «теорема схем».

Острова – отдельные фрагменты популяции, оптимизируемые на определённом интервале времени автономным и обменивающиеся частями популяций с помощью определённого протокола.

Теорема схем.

Пусть t – номер поколения. H – число примеров полезной схемы, M(H, t) - число реализаций схемы H поколений t.

Количество представителей схемы H в следующем поколение t+1 зависит от действия операции селекции и будет равно

, где

f_ср – средняя приспособленность популяции, f.

f(H) – средняя приспособленность тех строк в популяции, которые являются примерами H.

Отобранные представители полезной схемы H могут быть разрушены последующим кроссинговерам, при этом вероятность разрушения длинной последовательности больше, чем у короткой. Вероятность, что схема переживёт кроссовер не меньше:

Кроме кроссинговера разрушаемой операцией является операция мутации. Если вероятность мутации P_m, а порядок схемы O(H), то вероятность разрушения можно определить по формуле O(H)• P_m, тогда окончательно соотношение между поколениями будет следующими:

Таким образом, теорема схем утверждает сходимость генетического алгоритма к стандартному максимуму.

Общая сходимость генетического алгоритма к глобальному оптимуму не исключает обратного движения или деградации на отдельном участке развития генетического алгоритма.

Теорема о сходимости доказана только для стандартного генетического алгоритма, а для мобильного генетического алгоритма эволюционной стратегии сходимость не обеспечивается, поэтому в случае использования алгоритмов таких видов сходимость приводит только к рациональному, в лучшем случае, приемлемому решению. С учётом значительной вычислительной затратности генетического алгоритма их необходимо распараллелить, причём распараллеливание ведётся за счёт распределения различных фрагментов исходной популяции по вычислителя, в результате возникли так называемые вычислительные алгоритмы с использованием островов.