
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Курсовая стоимость и доходность облигаций. Дюрация Макколея.Содержание книги
Поиск на нашем сайте Стоимостная оценка облигаций Облигации имеют нарицательную цену (номинал) и рыночную цену. Номинальная стоимость облигации напечатана на самой облигации и обозначает сумму, которая берется взаймы и подлежит возврату по истечении срока облигационного займа. Рыночная цена облигаций определяется исходя из ситуации, сложившейся на рынке облигаций и финансовом рынке в целом к моменту продажи, а также двух главных элементов самого облигационного займа. Этими элементами являются: • перспектива получить при погашении номинальную стоимость облигации (чем ближе в момент покупки облигации срок ее погашения, тем выше ее рыночная стоимость); • право на регулярный фиксированный доход (чем выше доход, приносимый облигацией, тем выше ее рыночная стоимость). Курс облигаций Дисконт и процентный доход по облигации Общий доход от облигации складывается из следующих элементов: 1) Облигация, в отличие от акции, приносит владельцу фиксированный текущий доход. Этот доход представляет собой постоянный аннуитет — право получать фиксированную сумму ежегодно в течение ряда лет. Размер купонного дохода по облигациям зависит прежде всего от надежности облигации, иначе говоря, от того, кто является ее эмитентом. Чем устойчивее компания-эмитент и надежнее облигация, тем ниже предлагаемый процент. Кроме того, существует зависимость между процентным доходом и сроком обращения облигации: чем больше отдален срок погашения, тем выше должен быть процент, и наоборот. 2) Вторая составляющая дохода, приносимого облигацией - изменения стоимости облигации за соответствующий период: облигация, купленная по цене ниже номинала, т.е. с дисконтом. Примером таких облигаций, как уже говорилось ранее, служат облигации с нулевым купоном. Доход по ним образуется как разница между ценой, по которой они продаются, и номиналом облигации. При покупке и продаже облигаций с дисконтом важным моментом является определение цены продажи облигации. Иными словами: по какой цене следует продать облигацию сегодня, если известна сумма, которая будет получена в будущем (номинал), и базовая норма доходности (ставка рефинансирования). Подсчет этой цены называется дисконтированием, а сама цена — сегодняшней стоимостью будущей суммы денег.
3) Последний элемент совокупного дохода — доход от реинвестиций полученных процентов — присутствует лишь при условии, что полученный в виде процентов текущий доход по облигации постоянно реинвестируется. Данный вид дохода может иметь довольно существенное значение при покупке долгосрочных облигаций. Доходность облигаций В общем виде доходность представляет собой доход, приходящийся на единицу затрат. Различают текущую доходность и полную, или конечную, доходность облигаций. Показатель текущей доходности характеризует годовые (текущие) поступления по облигации относительно сделанных затрат на ее покупку
Скон = [ (Дсп+ P)/Кр*т ] * 100% где Cкон — конечная доходность облигаций, %; Дсп — совокупный процентный доход, руб.; Р — величина дисконта по облигации, руб.; Кр — курсовая стоимость облигации, по которой она была приобретена, руб.; n — число лет, в течение которых инвестор владел облигацией. Величина дисконта Р равна разнице между номинальной стоимостью облигации и ценой приобретения в случае, если инвестор держит облигацию до погашения. Существуют два важных фактора, влияющих на доходность облигаций. Это — инфляция и налоги. Дюрация (англ. duration — длительность) — это средневзвешенный срок потока платежей, взвешенный по дисконтированной сумме. Иными словами — это точка равновесия сроков дисконтированных платежей. Дюрация является важнейшей характеристикой потока платежей, определяющая его чувствительность к изменению процентной ставки. Понятие дюрации было введено американским ученым Ф. Маколи (F.R. Macaulay). Дюрация рассчитывается по формуле: Где PVi — Дисконтированная стоимость будущих платежей; Ti — период поступления 1,2,3,4…N; N — количество периодов (период может быть любым: день, неделя, месяц, 10 дней и т. д.). Дюрация облигации Дюрация помогает определить степень зависимости рыночной цены облигации от изменения процентной ставки. Дюрация облигации приблизительно равна величине изменения цены облигации при изменении процентной ставки (ставки дисконтирования) на один процент. Другими словами, дюрация — это эластичность цены облигации по процентной ставке (ставке дисконтирования). Чем больше дюрация ценной бумаги, тем значительнее изменения ее рыночной стоимости при изменении процентной ставки (ставки дисконтирования). Следовательно, чем больше дюрация, тем выше риск процентной ставки. Время, проходящее до наступления срока платежа по ценной бумаге, могло бы быть использовано для получения по этим инвестициям более высокого дохода. Следовательно, цена актива с более продолжительным сроком платежа имеет более сильную зависимость от процентной ставки (ставки дисконтирования), чем цена актива, по которому поток платежей происходит в ближайшем будущем. Ввиду существования такой зависимости, дюрация иногда измеряется как средневзвешенный срок до получения каждого платежа по ценной бумаге. Таким образом, дюрация бескупонной облигации со сроком погашения n лет — n лет, поскольку единственный платеж по ней будет произведен через n лет. При наличии купонных выплат, дюрация меньше чем n. Для облигаций дюрация рассчитывается следующим образом: Из этой формулы следуют следующие закономерности изменения дюрации: При прочих равных условиях, чем продолжительнее срок погашения облигации, тем больше дюрация. При прочих равных условиях, при повышении ставки дисконтирования дюрация купонных облигаций уменьшается. При прочих равных условиях, чем выше ставка купонных платежей по облигации, тем меньше дюрация. Математически дюрация Маколея находится по следующей формуле:
|
||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 191; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.01 с.) |

 Ko – курс облигаций, Kp – рыночная цена облигации, P – номинальная цена облигации.
Ko – курс облигаций, Kp – рыночная цена облигации, P – номинальная цена облигации.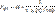 Kрд – цена продажи облигации с дисконтом, руб., H – номинальная цена облигации, руб., T – число лет, по истечении которых облигация будет погашена, C – норма ссудного процента (или ставка рефинансирования), %,
Kрд – цена продажи облигации с дисконтом, руб., H – номинальная цена облигации, руб., T – число лет, по истечении которых облигация будет погашена, C – норма ссудного процента (или ставка рефинансирования), %,  – дисконтный множитель, показывающий, какую долю составляет цена продажи облигации в ее номинальной цене.
– дисконтный множитель, показывающий, какую долю составляет цена продажи облигации в ее номинальной цене. Стек — текущая доходность облигации, %; Д — сумма выплачиваемых в год процентов, руб.; Кр — курсовая стоимость облигации, по которой она была приобретена, руб.
Стек — текущая доходность облигации, %; Д — сумма выплачиваемых в год процентов, руб.; Кр — курсовая стоимость облигации, по которой она была приобретена, руб.
 Где PVi — это текущая (дисконтированная)стоимость будущих поступлений (купоны и основной долг) по облигации, Ti — период поступления i-го дохода, Price — цена облигации.
Где PVi — это текущая (дисконтированная)стоимость будущих поступлений (купоны и основной долг) по облигации, Ti — период поступления i-го дохода, Price — цена облигации. n = количество денежных потоков, t = время до погашения, C = денежный поток, i = требуемая доходность, M = погашение номинальной стоимости, P = цена облигации, причем Р =
n = количество денежных потоков, t = время до погашения, C = денежный поток, i = требуемая доходность, M = погашение номинальной стоимости, P = цена облигации, причем Р = 



