
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обобщенная линейная модель множественной регрессии и обобщенный метод наименьших квадратов.Содержание книги
Поиск на нашем сайте
Одно из предположений классической линейной регрессионной модели состоит в том. Что случайные ошибки некоррелированы между собой и имеют постоянную дисперсию. В тех случаях, когда наблюдаемые объекты достаточно однородны, не сильно отличаются друг от друга, такое допущение оправдано. Однако во многих случаях такое предположение нереалистично. Например, если исследуется зависимость расходов на питание в семье от ее общего дохода, то естественно ожидать, что разброс в данных будет выше для семей с более высоким доходом. Это означает, что дисперсии зависимых величин (а следовательно, и случайных ошибок) не постоянны. Это явление в эконометрике называется гетероскедастичностью (в отличие от гомоскедастичности – равенства дисперсий). Кроме того, при анализе временных рядов в довольно редких случаях можно считать, что наблюдения некоррелированы во времени. Как правило, значение исследуемой величины в текущий момент времени статистически зависит от значений в прошлом, что означает наличие корреляции между ошибками. Поэтому естественно изучать модели регрессии без предположения, что Рассмотрим обобщенную регрессионную модель β – k ×1 вектор неизвестных параметров, ε – n ×1 вектор случайных ошибок, причем: 1) матрица X неслучайна и имеет полный ранг; 2) М(ε)=0; 3) 1. Обобщенный метод наименьших квадратов. Ответ на вопрос об эффективной линейной несмещенной оценке вектора β для модели (1) дает следующая теорема. Теорема Айткена. В классе линейных несмещенных оценок вектора β для обобщенной регрессионной модели оценка Использование термина «обобщенный метод наименьших квадратов» объясняется следующим соображением. Как получено при доказательстве теоремы Айткена, оценка Проблема применения обобщённого МНК заключается в неизвестности ковариационной матрицы случайных ошибок. Поэтому на практике используют доступный вариант ОМНК, когда вместо V (ковариационной матрицы) используется её некоторая оценка. Однако, и в этом случае возникает проблема: количество независимых элементов коварационной матрицы равно n(n+1)/2, где -количество наблюдений (для примера — при 100 наблюдениях нужно оценить 5050 параметров!). Следовательно, такой вариант не позволит получить качественные оценки параметров. На практике делаются дополнительные предположения о структуре ковариационной матрицы, то есть предполагается, что элементы ковариационной матрицы зависят от небольшого числа неизвестных параметров q. Их количество должно быть намного меньше числа наблюдений. Сначала применяется обычный МНК, получают остатки, затем на их основе оцениваются указанные параметры q. С помощью полученных оценок оценивают ковариационную матрицу ошибок и применяют обобщённый МНК с этой матрицей. В этом суть доступного ОМНК. Доказано, что при некоторых достаточно общих условиях, если оценки q состоятельны, то и оценки доступного ОМНК будут состоятельны.
|
||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 297; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.006 с.) |

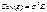 .
.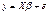 , (1) где у – n ×1 вектор зависимой переменной, X – n × k матрица независимых переменных,
, (1) где у – n ×1 вектор зависимой переменной, X – n × k матрица независимых переменных,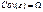 , и матрица Ω (омега) положительно определена. Иными словами, обобщенная модель отличается от классической только условием 3
, и матрица Ω (омега) положительно определена. Иными словами, обобщенная модель отличается от классической только условием 3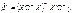 (4) имеет наименьшую матрицу ковариаций.
(4) имеет наименьшую матрицу ковариаций.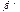 получается минимизацией по b (оценка вектора параметров β) сумм квадратов отклонений
получается минимизацией по b (оценка вектора параметров β) сумм квадратов отклонений 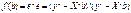 для системы (3), где е – фактические ошибки модели или остатки. Но
для системы (3), где е – фактические ошибки модели или остатки. Но 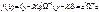 , т.е. для построения оптимальной оценки в модели (1) надо минимизировать «обобщенную» сумму квадратов отклонений
, т.е. для построения оптимальной оценки в модели (1) надо минимизировать «обобщенную» сумму квадратов отклонений 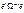 .
.


