
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классическая транспортная задача. Метод потенциалов.Содержание книги
Поиск на нашем сайте Транспортная задача (классическая) — задача об оптимальном плане перевозок однородного продукта из однородных пунктов наличия в однородные пункты потребления на однородных транспортных средствах (предопределённом количестве) со статичными данными и линеарном подходе (это основные условия задачи). Однородный продукт, сосредоточенный в m пунктах отправления в количествах a1…am единиц соответственно, необходимо доставить в каждый из n пунктов назначения в количествах b1…bn. Стоимость перевозки единицы из i-го пункта направления в j-й пункт назначения равна cij и известна для всех комбинаций (i, j). Пусть xij – количество продукта, перевозимого по маршруту (i, j). Задача заключается в определении таких величин xij для всех маршрутов (i, j), при которых суммарная стоимость перевозок была бы минимальной. Математическая модель транспортной задачи имеет следующий вид: найти наименьшее значение линейной функции
Для совместимости уравнений (2) и (3) необходимо, чтобы Теорема 1. Любая транспортная задача, для которой выполняется условие (5), имеет решение. Теорема 2. Система ограничений (2) и (3) содержит m+n-1 линейно независимых уравнений. Следствие 1. Существует опорное решение транспортной задачи, содержащее не более чем m+n-1 положительных перевозок xij. Теорема 3. Если предположить, что все ai и bj - неотрицательные целые числа, то любой опорный план состоит из целочисленных перевозок xij.
Все транспортные задачи записываются в виде табл.1 Клетки таблицы, в которых находятся отличные от нуля перевозки, называются занятыми, остальные – свободными. Занятые клетки соответствуют базисным неизвестным, и для невырожденного опорного решения их количество равно m+n-1. Циклом называется набор клеток (i1, j1) (i1, j2) (i2, j2)… (ik, jk) (il, jk), в котором две и только две соседние клетки расположены в одном столбце или в одной строке таблицы. Графически цикл представляет собой замкнутую ломанную линию. Допустимое решение будет опорным, если в таблице нельзя построить замкнутый цикл, все вершины которого расположены в занятых клетках. Всякое решение транспортной задачи, содержащее более m+n-1 занятых клеток, не является опорным. При таком решении в таблице всегда можно построить замкнутый цикл, с помощью которого уменьшают число занятых клеток до m+n-1. Метод потенциалов. Потенциалами опорного решения x = (xij) называют числа ui и vj (i= Потенциалы ui и vj (i= X – вектор-столбец XТ = (x11, x12,…, x1n, x21, x22,…, x2n,…, xm1, xm2,…, xmn). Тогда двойственная задача будет иметь вид: g(Y) = (Y, B) – max; при ограничениях YA£C. В нематричном представлении ограничения двойственной задачи записываются очень просто ui + vj £ cij (i= Теорема 4. Пусть ui и vj (i= Решение транспортной задачи методом потенциалов проводится по следующей схеме: 1) находим начальное опорное решение х1 = (х1ij) методами северо-западного угла (диагональный) или наименьшего элемента; 2) вычисляем потенциалы ui и vj (i= 3) в таблице строим цикл, одна вершина которого находится в клетке (k, l), а все остальные вершины – в занятых клетках. Далее, вершину в клетке (k, l), метим знаком "+", остальные – знаками "-" и "+" так, чтобы они от вершины к вершине чередовались. Обозначим через q наименьшее из чисел х1ij, стоящих в клетках, помеченных знаком "-"; пусть q = хrs (если такое число находится в нескольких клетках, то выберем ту из них, которой соответствует наибольшее значение сij). После этого заполняем таблицу согласно следующему правилу: а) клетки, не являющиеся вершинами цикла, остаются без изменения; б) если клетка (i, j) помечена знаком "+", то в нее записывают число х1ij + q; в) клетка (r, s) становится свободной, ее не заполняют, а в остальные клетки (i, j), помеченные знаком "-", записывают число х1ij - q. В результате получаем ациклический набор из m+n-1 занятых (базисных) клеток таблицы, который определяет опорное решение х2 такое, что f(х2)£f(х1). Принимая х2 за исходное опорное решение, повторяем п.2 и п.3 до тех пор, пока не будет найдено оптимальное решение задачи.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 167; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.006 с.) |

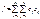 -> min (1)при ограничениях
-> min (1)при ограничениях 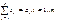 (2)
(2)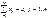 , (3)
, (3)  (4)
(4)  (5) Такая модель называется закрытой. Когда суммарный объём предложений (грузов, имеющихся в пунктах отправления) не равен общему объёму спроса на товары (грузы), запрашиваемые пунктами потребления, транспортная задача называется несбалансированной (открытой).
(5) Такая модель называется закрытой. Когда суммарный объём предложений (грузов, имеющихся в пунктах отправления) не равен общему объёму спроса на товары (грузы), запрашиваемые пунктами потребления, транспортная задача называется несбалансированной (открытой).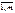 , j=
, j=  ) такие, что ui+ vj=сij для всех занятых клеток. Так как количество занятых клеток m+n-1, то для определения потенциалов надо решить систему m+n-1 линейных уравнений с m+n неизвестными. Эта система всегда совместна, причем одно из неизвестных можно положить равным любому числу и тогда все остальные неизвестные определяются однозначно.
) такие, что ui+ vj=сij для всех занятых клеток. Так как количество занятых клеток m+n-1, то для определения потенциалов надо решить систему m+n-1 линейных уравнений с m+n неизвестными. Эта система всегда совместна, причем одно из неизвестных можно положить равным любому числу и тогда все остальные неизвестные определяются однозначно.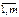 , j=
, j= 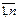 ) можно интерпретировать как двойственные переменные транспортной задачи. Составить двойственную задачу линейного программирования к прямой задаче (1) – (5). С этой целью ограничения (2), (3) представим в матричной форме AX = B, где матрица А состоит из нулей и единиц и имеет размерность (m+n) x mn. Матрицу А, вектор В и вектор-строку Y двойственных переменных для
) можно интерпретировать как двойственные переменные транспортной задачи. Составить двойственную задачу линейного программирования к прямой задаче (1) – (5). С этой целью ограничения (2), (3) представим в матричной форме AX = B, где матрица А состоит из нулей и единиц и имеет размерность (m+n) x mn. Матрицу А, вектор В и вектор-строку Y двойственных переменных для  наглядности
наглядности 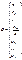 можно
можно  определить формулами:
определить формулами: 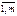 , j=
, j= 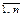 )
) ) – потенциалы опорного решения x = (xij) транспортной задачи. Если для всех свободных клеток (i, j) оценки sij= cij – (ui + vj) > 0, то х – оптимальное решение задачи.
) – потенциалы опорного решения x = (xij) транспортной задачи. Если для всех свободных клеток (i, j) оценки sij= cij – (ui + vj) > 0, то х – оптимальное решение задачи. , j=
, j= 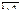 ) опорного решения х1. Если для всех свободных клеток (i, j) sij= cij – (ui + vj) > 0, то х – оптимальное решение и задача решена. В противном случае выбираем клетку (k, l), соответствующую наименьшему значению sij;
) опорного решения х1. Если для всех свободных клеток (i, j) sij= cij – (ui + vj) > 0, то х – оптимальное решение и задача решена. В противном случае выбираем клетку (k, l), соответствующую наименьшему значению sij;


