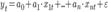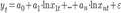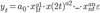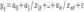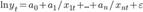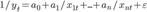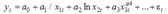Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эконометрическая модель фирмы.Содержание книги
Поиск на нашем сайте
При построении эконометрических моделей могут использоваться два принципиально различных типа исходных информационных массивов — статический и динамический. Статический массив выражает взаимосвязи между результирующей (зависимой, объясняемой и т.п.) переменной y и влияющими на нее факторами (независимыми, объясняющими переменными) xi, характерными для однородной совокупности объектов в определенный период времени. Примером таких объектов является некоторая совокупность однотипных промышленных предприятий (заводов одной отраслевой направленности). В качестве y в практических исследованиях часто рассматриваются показатели производительности труда, объемов выпускаемой продукции и некоторые другие. В качестве xi — влияющие на уровень этих показателей факторы — объемы используемых фондов, квалификация рабочей силы и т.п. Таким образом, необходимая для построения эконометрической модели статическая информация выражается следующими массивами взаимно соответствующих наборов данных: yj — уровень зависимой переменной на j-м объекте совокупности; xij — уровень фактора i-го фактора на j-м объекте совокупности; i = 1, 2,..., n; j = 1, 2,..., N. В общем случае эконометрическая модель, использующая динамическую информацию, связывает значения некоторой зависимой переменной y в моменты времени t cо значениями независимых переменных (факторов) xit, рассматриваемых в те же моменты времени (или в предшествующие). Такая информация может отражать, например, уровни производительности труда на одном из заводов и определяющие ее характеристики факторов в последовательные моменты времени. Несложно заметить, что принципиального различия между статическим и динамическим массивами не существует. Будем предполагать, что общее число независимых факторов равно n, i = 1, 2,..., n, и в ходе измерения уровней всех переменных в моменты времени t = 1, 2,..., T был сформирован массив исходных данных, который послужит основой для построения эконометрической модели. Данный массив образован вектором-столбцом значений зависимой переменной y = (y1, y2,..., yT)' и матрицей значений независимых переменных
Эконометрическая модель, отражающая взаимосвязь переменных y и xi, ft (a, x) — функционал, выражающий закономерность взаимосвязи между переменными xit и yt; x = (х1, х2,..., хn) — вектор независимых переменных (факторов); a = (a0, a1,..., an) — вектор параметров модели; параметр ai выражает степень влияния фактора xi на переменную y; a0 — постоянная модели; εt- случайная ошибка модели в момент t, в отношении которой выдвигается предположение о равенстве нулю ее математического ожидания и конечности дисперсии. Под структурой эконометрической модели понимается совокупность переменных и их взаимосвязей, входящих в правую часть выражения (1.1). Форма эконометрической модели отражает особенности взаимосвязи между переменными y и xi, Проблема построения эконометрической модели состоит в определении конкретного состава независимых переменных xi, выборе вида функционала, связывающего их с зависимой переменной y и в оценке его параметров ai; на основании известных компонент вектора y и элементов матрицы Х. Состав переменных xi и функционал f могут отражать либо экономическую концепцию, лежащую в основе взаимосвязи между зависимой и независимыми переменными, либо эмпирические (т.е. выявленные в ходе конкретных исследований) взаимосвязи между ними в периоде. В практике эконометрических исследований используется достаточно широкий круг функциональных зависимостей между переменными. Основные из них следующие: 1. линейная эконометрическая модель 2. правая полулогарифмическая эконометрическая модель 3. степенная эконометрическая модель 4. гиперболическая эконометрическая модель 5. логарифмическая гиперболическая эконометрическая модель 6. обратная линейная (функция Торнквиста) эконометрическая модель
7. функция с постоянной эластичностью замены Следует отметить, что в практических исследованиях могут встретиться и комбинации рассмотренных выше зависимостей. Пример. 1) Затраты, выручка, прибыль в краткосрочном периоде P – цена производителя; Q – объем производства; B – выручка; П – прибыль; TC – общие затраты; FC – постоянные, VC – переменные (AVC=VC/Q – предельные переменные затраты, на единицу продукции) Затраты: TC=FC+VC= FC+AVC*Q; Выручка: В=P*Q Прибыль: П=В-TC=P*Q-FC-AVC*Q=-FC+(P-AVC)*Q, т.е. y = a + bx + e – эконометрическая модель фирмы, где X – независимая переменная, сопоставленная объему продаж Q Y – зависимая переменная, сопоставленная прибыли П A – свободный член уравнения регрессии, сопоставленный постоянным издержкам в краткосрочном периоде B – коэффициент уравнения регрессии, равный выражению Цена за минусом предельных переменных издержек (P-AVC) E – ошибка уравнения регрессии.
1) Затраты, выручка, прибыль в долгосрочном периоде. Основное отличие долгосрочного периода от краткосрочного в том, что условно постоянные издержки становятся зависимыми от объема продаж (т.е. переходят в категорию переменных) ввиду обновления производственных мощностей, перехода на новую технологию, движения научно-технического прогресса, расширения производственных площадей и др.факторов. Тогда модель примет вид: Затраты: LTC=LFC(Q)+LVC(Q)=LAFC*Q+LAVC*Q (буква L – longterm, долгосрочный); Выручка: В=P*Q Прибыль: П=В-TC=P*Q- LFC(Q)-LVC(Q)=(P-LAFC-LAVC)*Q, т.е. y = a + b 1 x 1+ b 2 x 2+ e – эконометрическая модель фирмы, где X1 – независимая переменная, сопоставленная объему продаж Q, X2 – независимая переменная, сопоставленная имеющейся технологии Т Y – зависимая переменная, сопоставленная прибыли П A – свободный член уравнения регрессии, вероятнее всего статистически незначимый в данном уравнении B1 – коэффициент уравнения регрессии, равный выражению Цена за минусом полных предельных издержек (P-LAFC-LAVC)=(P-LATC) B2 – коэффициент уравнения регрессии при переменной Технология E – ошибка уравнения регрессии.
|
||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 136; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.130.119 (0.01 с.) |

 Эконометрическая модель (econometric model) - это статистическая модель, которая является средством прогнозирования значений определенных переменных, называемых эндогенными переменными (endogenous variables). Для того чтобы сделать такие прогнозы, в качестве исходных данных используются значения других переменных, называемых экзогенными переменными (exogenous variables). Предположения о значениях таких переменных делаются пользователем модели.
Эконометрическая модель (econometric model) - это статистическая модель, которая является средством прогнозирования значений определенных переменных, называемых эндогенными переменными (endogenous variables). Для того чтобы сделать такие прогнозы, в качестве исходных данных используются значения других переменных, называемых экзогенными переменными (exogenous variables). Предположения о значениях таких переменных делаются пользователем модели. размерностью T*n, таким образом, что каждому элементу yt вектора y соответствует строка матрицы Х.
размерностью T*n, таким образом, что каждому элементу yt вектора y соответствует строка матрицы Х.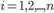 , в общем виде может быть представлена следующим уравнением: yt = ft (a, x) + εt, (1.1)
, в общем виде может быть представлена следующим уравнением: yt = ft (a, x) + εt, (1.1)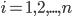 .
.