
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модель межотраслевого баланса Леонтьева.Содержание книги
Поиск на нашем сайте
Центральная идея межотраслевого баланса заключается в том, что каждая отрасль в нем рассматривается и как производитель и как потребитель. Она представляет собой единую взаимоувязанную систему информации о взаимных поставках продукции между всеми отраслями производства, а также об объеме и отраслевой структуре основных производственных фондов, об обеспеченности народного хозяйства ресурсами труда и т. д. В основе исследований балансовых моделей лежат балансовые таблицы, содержащие данные о производстве и потреблении продукции различных отраслей или предприятий. Характерные черты и особенности этого метода описываются с помощью матричных моделей баланса. Из математических методов здесь главным образом используется аппарат линейной алгебры. Двухотраслевая модель межотраслевого баланса. Пусть исполнение баланса за предшествующий период характеризуется данными, приведенными в табл.:
Продукция каждой отрасли частично идет на внешнее потребление (конечный продукт), а частично используется в качестве сырья, полуфабрикатов или других средств производства в других отраслях, в том числе и в данной. Эту часть продукции называют производственным потреблением. Поэтому каждая из рассматриваемых отраслей выступает и как производитель продукции (i-я строка таблицы), и как ее потребитель (j-й столбец таблицы). Обозначим через xi валовый выпуск продукции i-й отрасли за планируемый период и через yi — конечный продукт, идущий на внешнее для рассматриваемой системы потребление (средства производства других экономических систем, потребление населения, образование запасов и т. д.). Таким образом, разность xi-yi составляет часть продукции i-й отрасли, которая предназначена для внутрипроизводственного потребления. Предполагаем, что баланс составляется в стоимостном разрезе. Обозначим через xij часть продукции i-й отрасли, которая потребляется j-й отраслью для обеспечения выпуска ее продукции в размере xi. Очевидно, величины, расположенные в строках, связаны следующими балансовыми равенствами
Одна из задач балансовых исследований заключается в том, чтобы на базе данных об исполнении баланса за предшествующий период определить исходные данные на планируемый период. Рассчитаем по данным таблицы коэффициенты прямых затрат. Это отношение количества продукции i-й отрасли, поступающей в j-ю отрасль для обеспечения выпуска ее продукции в размере xj т. е.
т. е. затраты i-й отрасли в j-ю отрасль пропорциональны ее валовому выпуску или, другими словами, зависят линейно от валового выпуска xj. Выписанные соотношения называют условием линейности прямых затрат:
Найденные коэффициенты образуют матрицу прямых затрат Все элементы aij этой матрицы неотрицательны. Это записывается в виде матричного неравенства A>=0. Заданием матрицы А определяются все внутренние взаимосвязи между производством и потреблением, характеризуемые таблицей выше. Теперь можно записать линейную балансовую модель, соответствующую данным табл., если подставить значения В матричной форме (E - A) X = Y, где Эта система двух уравнений может быть использована для определения x1 и x2 при заданных значениях y1 и y2, для исследования влияния на валовый выпуск любых изменений в ассортименте конечного продукта, для определения матрицы коэффициентов полных затрат, элементы которой служат важными показателями для планирования развития отраслей и т. д.
Пример расчета межотраслевого баланса Рассмотрим 2 отрасли промышленности: производство угля и стали. Уголь требуется для производства стали, а некоторое количество стали — в виде инструментов — нужно для добычи угля. Предположим, что условия таковы: для производства 1 т стали нужно 3 т угля, а для 1 т угля — 0,1 т стали.
Отрасль Уголь Сталь Уголь 1 3 Сталь 0.1 1
Мы хотим, чтобы чистый выпуск угольной промышленности был 200 тыс. тонн угля, а чёрной металлургии — 50 тыс. тонн стали (это наши y1 и y2). Если каждая из них будет производить лишь 200 тыс. и 50 тыс. тонн, то часть продукции будет использоваться в другой отрасли (следовательно, на конечное потребление останется гораздо меньше угля и стали). Для производства 50 тыс. тонн стали требуется 50*3 = 150 тыс. тонн угля, а для производства 200 тыс. тонн угля нужно 200*0.1 = 20 тыс. тонн стали. Чистый выход будет равен: 200-150 = 50 тыс.тонн угля и 50-20 = 30 тыс. тонн стали. Нужно дополнительно производить уголь и сталь, чтобы использовать их в другой отрасли. Обозначим х1 — количество угля, х2 — количество стали. Валовый выпуск каждой продукции найдем из системы уравнений:
|
||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 142; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.221.114 (0.009 с.) |


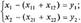
 где
где 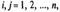
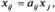
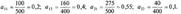
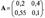
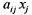 в балансовые равенства
в балансовые равенства 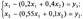
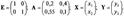
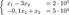 Решение: 500 000 т угля и 100 000 т стали.
Решение: 500 000 т угля и 100 000 т стали.


