
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение обобщенного Метода оценивания параметров моделей на практике (некоторые случаи).Содержание книги
Поиск на нашем сайте А) Эконометрические модели с коррелирующими ошибками При наличии автокорреляционных взаимосвязей в ряду ошибки ковариационная матрица формально может быть представлена в виде:
Можно воспользоваться следующим практическим подходом к оценке недиагональной ковариационной матрицы ошибок эконометрической модели, отражающей существование корреляционной зависимости между ее значениями. Этот подход не требует предварительной информации относительно характера взаимосвязей между ее последовательными значениями 1) на основании исходных данных – вектора у и матрицы Х – формируется уравнение эконометрической модели, затем с помощью МНК оцениваются ее параметры, определяется вектор фактической ошибки е, значения которого проверяют с помощью критериев (например, Дарбина – Уотсона) на наличие автокорреляции. В том случае, если факт корреляции установлен, то на основе эмпирического ряда ошибки 2) определенную таким образом ковариационную матрицу фактической ошибки Процедура построения модели завершается, если критерий Дарбина – Уотсона не подтверждает наличие автокорреляции в ряду ошибок очередного этапа оценивания модели. На практике чаще всего достаточно произвести одну итерацию. Б) Эконометрические модели с гетероскедастичными ошибками В случае гетероскедастичности ошибок ковариационная матрица имеет вид:
Для эконометрических моделей с гетероскедастичными ошибками может быть применена процедура последовательных этапов расчетов, как и в случае автокорреляции между ошибками модели. Для этого на первом этапе по результатам применения обыкновенного МНК должны быть сформированы оценки При таком предположении оценки дисперсий Подобная процедура может быть реализована при любых правдоподобных гипотезах о закономерности изменения дисперсии ошибок, например, для квадратичной закономерности, для логарифмической зависимости и т.д.
|
||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 152; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.007 с.) |

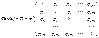
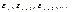 . Согласно этому подходу матрица Cov (e) рассматривается как оценка ковариационной матрицы истинной ошибки модели Cov (ε), находится эмпирическим путем в несколько этапов:
. Согласно этому подходу матрица Cov (e) рассматривается как оценка ковариационной матрицы истинной ошибки модели Cov (ε), находится эмпирическим путем в несколько этапов: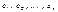 оцениваются элементы ее ковариационной матрицы по формуле
оцениваются элементы ее ковариационной матрицы по формуле 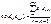 , k =1, 2,…
, k =1, 2,…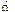 используют для оценки параметров той же модели с помощью ОМНК (формула (4)). Далее вычисляется новый ряд фактической ошибки, происходит проверка на наличие автокорреляции и, в случае подтверждения этой гипотезы, определяется новая матрица
используют для оценки параметров той же модели с помощью ОМНК (формула (4)). Далее вычисляется новый ряд фактической ошибки, происходит проверка на наличие автокорреляции и, в случае подтверждения этой гипотезы, определяется новая матрица 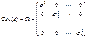
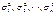 матрицы Cov (e). Сделать это на основе значений фактической ошибки
матрицы Cov (e). Сделать это на основе значений фактической ошибки 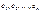 для каждой точки t = 1, 2,…, n невозможно. Вследствие этого приходится привлекать некоторые дополнительные гипотезы относительно характера изменения дисперсии ошибки, например, гипотезу о линейном законе ее изменения.
для каждой точки t = 1, 2,…, n невозможно. Вследствие этого приходится привлекать некоторые дополнительные гипотезы относительно характера изменения дисперсии ошибки, например, гипотезу о линейном законе ее изменения.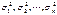 могут быть определены следующим образом. Для двух непересекающихся интервалов
могут быть определены следующим образом. Для двух непересекающихся интервалов 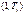 и
и 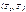 по значениям фактических ошибок
по значениям фактических ошибок 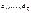 и
и 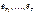 могут быть получены оценки дисперсий
могут быть получены оценки дисперсий 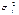 и
и 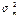 , которые соотносятся с моментами t = l и t = m, являющимися серединами этих рядов. Далее на основе этих двух значений строится линейная зависимость
, которые соотносятся с моментами t = l и t = m, являющимися серединами этих рядов. Далее на основе этих двух значений строится линейная зависимость 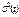 , аппроксимирующая изменение дисперсии на интервале (1, T). Каждое из найденных значений
, аппроксимирующая изменение дисперсии на интервале (1, T). Каждое из найденных значений 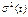 будет представлять собой оценку соответствующего элемента диагональной матрицы Ω. Эта матрица затем используется на втором этапе вычислений оценок параметров модели при помощи ОМНК.
будет представлять собой оценку соответствующего элемента диагональной матрицы Ω. Эта матрица затем используется на втором этапе вычислений оценок параметров модели при помощи ОМНК.


