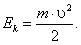Силы трения. Коэффициент трения

Классификация основных видов трения

 

При соприкосновении движущихся (или приходящих в движение) тел с другими телами, а также с частицами вещества окружающей среды возникают силы, препятствующие такому движению. Эти силы называют силами трения. Действие сил трения всегда сопровождается превращением механической энергии во внутреннюю и вызывает нагревание тел и окружающей их среды.

 

Существует внешнее и внутреннее трение (иначе называемое вязкостью). Внешним называют такой вид трения, при котором в местах соприкосновения твердых тел возникают силы, затрудняющие взаимное перемещение тел и направленные по касательной к их поверхностям.

Внутренним трением (вязкостью) называется вид трения, состоящий в том, что при взаимном перемещении слоев жидкости или газа между ними возникают касательные силы, препятствующие такому перемещению.

Внешнее трение подразделяют на трение покоя (статическое трение) и кинематическое трение. Трение покоя возникает между неподвижными твердыми телами, когда какое-либо из них пытаются сдвинуть с места. Кинематическое трение существует между взаимно соприкасающимися движущимися твердыми телами. Кинематическое трение, в свою очередь, подразделяется на трение скольжения и трение качения.

 

В жизни человека силы трения играют важную роль. В одних случаях он их использует, а в других борется с ними. Силы трения имеют электромагнитную природу.

 

Трение покоя

Наблюдения показывают, что сила трения покоя всегда направлена противоположно действующей на тело внешней силе, стремящейся привести это тело в движение. До определенного момента сила трения покоя увеличивается с возрастанием внешней силы, уравновешивая последнюю. Максимальное значение силы трения покоя пропорционально модулю силы Fд давления, производимого телом на опору.

 

По третьему закону Ньютона сила Fд давления тела на опору равна по модулю силе N реакции опоры. Поэтому максимальная сила трения покоя пропорциональна силе реакции опоры. Для модулей этих сил справедливо следующее соотношение:

F_п=f_пN

 

где f_п - безразмерный коэффициент пропорциональности, называемый коэффициентом трения покоя. Значение этого коэффициента зависит от материала и состояния трущихся поверхностей.

Рис.3

Определить значение коэффициента трения покоя можно следующим образом. Пусть тело (плоский брусок) лежит на наклонной плоскости АВ (рис. 3). На него действуют три силы: сила тяжести F, сила трения покоя Fп и сила реакции опоры N. Нормальная составляющая Fп силы тяжести представляет собой силу давления Fд, производимого телом на опору.

Тангенциальная составляющая Fт силы тяжести представляет собой силу, стремящуюся сдвинуть тело вниз по наклонной плоскости.

При малых углах наклона сила Fт уравновешивается силой трения покоя Fп и тело на наклонной плоскости покоится (сила N реакции опоры по третьему закону Ньютона равна по модулю и противоположна по направлению силе Fд, т. е. уравновешивает ее).

 

Виды кинематического трения

Трение скольжения

Трение скольжения возникает при скольжении одного твердого тела по поверхности другого. Закон для трения скольжения имеет вид

F_c= f_cN

 

где F_c - модуль силы трения скольжения; f_c - безразмерный коэффициент трения скольжения; N - модуль силы реакции опоры. Значение f_c зависит от того, из каких веществ изготовлены трущиеся поверхности и от качества их обработки. Если сделать поверхности более гладкими, значение fc уменьшится. Однако уменьшать шероховатость поверхностей можно лишь до определенного предела, так как при очень гладких (например, полированных) поверхностях значение fc вновь увеличивается. Происходит это потому, что молекулы тел с гладкими поверхностями близко подходят друг к другу и силы молекулярного притяжения между ними вызывают "прилипание" тел.

 

 

Задачи

 

1. Найдите удлинение буксирного троса жесткостью 100 кН/м при буксировке автомобиля массой 2 тонны с ускорением 0,5 м/с² Трением пренебречь.

Дано:

m = 2 т. = 2000 кг

а = 0,5 м/с²

х = 100 кН/м = 100000 Н/м

Найти: ΔL

Решение:

По третьему закону Ньютона сила, растягивающая трос, равна силе, действующей на автомобиль. В отсутствие силы трения на автомобиль в горизонтальном направлении другие силы не действуют, поэтому:

mа = F

Запишем для троса закон Гука: F = kΔl

mа = kΔl отсюда получим: Δl = mа/k = 2000 · 0,5/100000 = 0,01 м.

 

2. Оцените значение силы взаимного тяготения двух кораблей, удаленных друг от друга на 100 м, если масса каждого из них по 10000 т.

Дано:

m = 10000 т = 10 000 000 кг = 1·10⁷ кг

R = 100 м

Найти: F -?

Решение:

Из закона всемирного тяготения:

F = G·M_1·M₂ / R²

G – гравитационная постоянная равна – 6,67·10^-11 Н·м² /кг²

F = 6,67·10^-11 ·1·10^7·1·10⁷/ 100² = 1 Н

 

 

Закон сохранения импульса

 

Импульс материальной точки

 

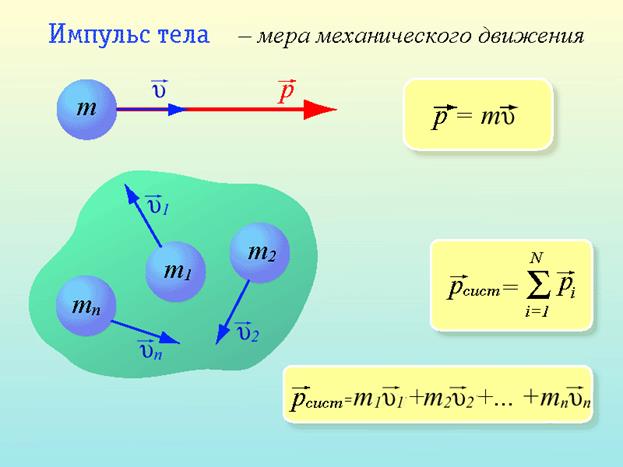
Основную задачу механики - определение положения тела в любой момент времени - можно решить с помощью законов Ньютона, если известны силы, действующие на тело, как функции координат и времени. На практике эти зависимости не всегда известны. Однако многие задачи в механике можно решить, не зная значений сил, действующих на тело. Это возможно в том случае, если известны величины, характеризующие механическое движение тел и сохраняющиеся при определенных условиях. Такими величинами являются импульс, механическая энергия и момент импульса.

Импульсом тела (материальной точки) называют векторную величину, равную произведению массы тела на его скорость:

Единицей измерения импульса в СИ является 1 кг·м/с. Импульс тела направлен в ту же сторону, что и скорость тела.

 

 

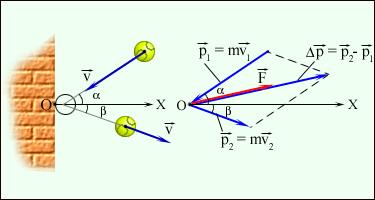
Изменение импульса

В случае прямолинейного равномерного движения тела постоянной массы импульс тела остается величиной постоянной, если скорость или масса тела в процессе движения меняются, то импульс тела также меняется.

Изменение импульса тела равно:

Δр = F·Δt

Изменение импульса материальной точки пропорционально приложенной к ней силе и имеет такое же направление, как и сила.

Импульс тела является векторной величиной, и для правильного нахождения изменения импульса тела необходимо применять правила вычитания векторов. Так, например, при ударе тела массой m, движущегося со скоростью V, о неподвижную стенку изменение импульса тела показано на рисунке.

 

 

Если величина скорости тела при ударе не меняется, удар называется абсолютно упругим. В этом случае угол падения тела на стенку равен углу отражения тела.

Абсолютно неупругим называется такое столкновение, после которого, оба сталкивающихся тела движутся как единое целое и тем самым приобретают одинаковые скорости.

 

 

Закон сохранения импульса

При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, то такая система называется замкнутой.

В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.

Геометрическая (векторная) сумма импульсов взаимодействующих тел, составляющих замкнутую систему, остается неизменной.

Это равенство означает, что в результате взаимодействия двух тел их суммарный импульс не изменился. Рассматривая теперь всевозможные парные взаимодействия тел, входящих в замкнутую систему, можно сделать вывод, что внутренние силы замкнутой системы не могут изменить ее суммарный импульс, т. е. векторную сумму импульсов всех тел, входящих в эту систему.

Этот фундаментальный закон природы называется законом сохранения импульса. Он является следствием из второго и третьего законов Ньютона.

 

Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны. Примером может служить реактивное движение.

 

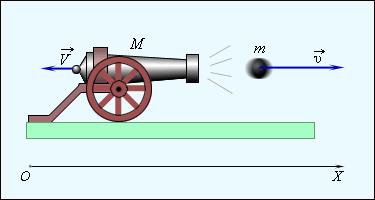
При стрельбе из орудия возникает отдача – снаряд движется вперед, а орудие – откатывается назад. Снаряд и орудие – два взаимодействующих тела. Скорость, которую приобретает орудие при отдаче, зависит только от скорости снаряда и отношения масс. Если скорости орудия и снаряда обозначить через V и v а их массы через M и m, то на основании закона сохранения импульса можно записать в проекциях на ось OX:

 

M· V + m· v = 0 Отсюда: V = - m· v / M

 

 

Задачи

 

1. Два шара с массами 0,5 кг и 0,3 кг движутся по гладкой горизонтальной поверхности навстречу друг другу со скоростями 2 м/с и 4 м/с. Найдите их скорость после центрального абсолютно неупругого удара.

Дано:

m₁ = 0,5 кг

m₂ = 0,3 кг

v₁ = 2 м/с

v₂ = 4 м/с

Найти: v -?

Решение:

Согласно закону сохранения импульса: m_1·v_{1 +} m_2·v₂ = (m₁ + m ₂) v

Т.к. при проекции на ось ОХ направление скорости одного из шаров отрицательно, то

v = m_1·v₁ -m_2·v₂ / m₁ + m ₂ = 0,5 · 2 - 0,3 · 4/ 0,5 + 0,3 = - 0,25 м/с

 

2. Неподвижный вагон массой 2·10⁴ кг сцепляется с платформой массой 3·10⁴ кг. До сцепки платформа имела скорость 1 м/с. Какова скорость вагона и платформы после их сцепки?

Решение: m_1·v_{1 +} m_2·v₂ = (m₁ + m ₂) v

Отсюда v = m_1·v₁ +m_2·v₂ / m₁ + m ₂ = 2·10⁴ · 0 + 3·10⁴ · 1/(2 + 3)· 10⁴ = 0,6 м/с

 

3. На платформу массой 500 кг, движущейся по горизонтальному пути со скоростью 0,2 м/с, насыпали 100 кг щебня. Какой стала скорость платформы?

Решение: m_1·v_{1 +} m_2·v₂ = (m₁ + m ₂) v

Отсюда v = m_1·v₁ +m_2·v₂ / m₁ + m ₂ = 500· 0,2/500+100 = 0,17 м/с

 

4. С какой скоростью должна лететь хоккейная шайба массой 160 г., чтобы ее импульс был равен импульсу пули массой 8 г., летящей со скоростью 600 м/с?

Решение:

Импульс пули равен Р_п = m_п v_п

Импульс шайбы Р_ш = m_ш v_ш

Т.к. импульс шайбы равен импульсу пули, то m_п v_п = m_ш v_ш Отсюда v_ш = m_п v_п/ m_ш =

0,008 · 600 / 0,16 = 30 м/с

 

5. Поезд массой 2000 т, двигаясь прямолинейно, увеличил скорость от 36 до 72 км/ч. Найти изменение импульса.

Решение: Найдем модуль импульса поезда по формуле Р= mv

Р₁ = mv₁ = 2· 10⁶ · 10 = 2· 10⁷ кг · м/с

Р₂ = mv₂ = 2· 10⁶ · 20 = 4· 10⁷ кг · м/с

Изменение импульса Δ Р= Р₂ – Р₁ = (4 – 2) · 10⁷ кг · м/с

 

Кинетическая и потенциальная энергия

 

Энергия – самая важная сохраняющаяся величина не только в механике, но и в физике.

Энергией называется скалярная физическая величина, являющаяся единой мерой различных форм движения материи и мерой перехода движения материи из одних форм в другие.

Для характеристики различных форм движения материи вводятся соответствующие виды энергии, например: механическая, внутренняя, энергия электростатических, внутриядерных взаимодействий и др.

Энергия подчиняется закону сохранения, который является одним из важнейших законов природы.

Механическая энергия Е характеризует движение и взаимодействие тел и является функцией скоростей и взаимного расположения тел. Она равна сумме кинетической и потенциальной энергий.

Работа силы

Работа совершается в природе всегда, когда на какое-либо движущееся тело действует сила. Например: сила тяготения совершает работу при падении капель дождя или камня с обрыва; сила упругости, когда распрямляется согнутое ветром дерево и т.д.

Работа силы равна произведению модулей силы и перемещения тела.

А = F·Δr

Работа является скалярной величиной. Она может быть положительной, отрицательной и равной нулю. Единицей измерения работы является джоуль: 1 Дж = 1Н· 1м

 

Кинетическая энергия

 

Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела.

 

Кинетическая энергия обозначается буквой E_k.

 

Теорема о кинетической энергии:

работа равнодействующей сил, приложенных к телу, равна изменению кинетической энергии тела.

A = Ek₂ – Ek₁.

Так как изменение кинетической энергии равно работе силы, кинетическая энергия тела выражается в тех же единицах, что и работа, т. е. в джоулях.

Если начальная скорость движения тела массой m равна нулю и тело увеличивает свою скорость до значения υ, то работа силы равна конечному значению кинетической энергии тела:

 

Физический смысл кинетической энергии:

кинетическая энергия тела, движущегося со скоростью υ, показывает, какую работу должна совершить сила, действующая на покоящееся тело, чтобы сообщить ему эту скорость.

 

Потенциальная энергия

 

Потенциальная энергия – это энергия взаимодействия тел.

Потенциальная энергия поднятого над Землей тела – это энергия взаимодействия тела и Земли гравитационными силами. Потенциальная энергия упруго деформированного тела – это энергия взаимодействия отдельных частей тела между собой силами упругости.

Потенциальными называются силы, работа которых зависит только от начального и конечного положения движущейся материальной точки или тела и не зависит от формы траектории.

При замкнутой траектории работа потенциальной силы всегда равна нулю. К потенциальным силам относятся силы тяготения, силы упругости, электростатические силы и некоторые другие.

Физическую величину, равную произведению массы тела на модуль ускорения свободного падения и на высоту, на которую поднято тело над поверхностью Земли, называют потенциальной энергией взаимодействия тела и Земли.

Потенциальная энергия обозначается буквой Ер:

Ep = m∙g∙h.

Работа силы тяжести при перемещении тела массой m из точки, расположенной на высоте h2, в точку, расположенную на высоте h1 от поверхности Земли, по любой траектории равна изменению потенциальной энергии взаимодействия тела и Земли, взятому с противоположным знаком.

А= – (Ер₂ – Ер₁).

 

Значение потенциальной энергии тела, поднятого над Землей, зависит от выбора нулевого уровня, т. е. высоты, на которой потенциальная энергия принимается равной нулю. Обычно принимают, что потенциальная энергия тела на поверхности Земли равна нулю.

 

Физический смысл потенциальной энергии взаимодействия тела с Землей:

потенциальная энергия тела, на которое действует сила тяжести, равна работе, совершаемой силой тяжести при перемещении тела на нулевой уровень.

 

В отличие от кинетической энергии поступательного движения, которая может иметь лишь положительные значения, потенциальная энергия тела может быть как положительной, так и отрицательной. Тело массой m, находящееся на высоте h, где h < h0 (h0 – нулевая высота), обладает отрицательной потенциальной энергией:

Еp = –m∙gh