
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Базовые соотношения систем массового обслуживанияСодержание книги
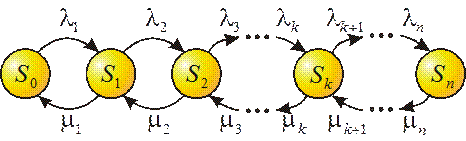
Поиск на нашем сайте Схема гибели и размножения Граф состояний для схемы гибели и размножения имеет вид, показан на рисунке 3.5.
Рисунок 3.5 - Схема гибели и размножения
Особенность этого графа в том, что все состояния системы можно вытянуть в одну цепочку, в которой каждое из средних состояний (S1, S2,...,Sn-1) связано прямой и обратной стрелкой с каждым из соседних состояний – правым и левым, а крайние состояния (S0,Sn) – только с одним соседним состоянием. Термин «схема гибели и размножения» ведет начало от биологических задач, где подобной схемой описывается изменение численности популяции. Пользуясь графом рисунка 3.5, составим и решим алгебраические уравнения Колмогорова для финальных вероятностей состояний. Для состояния S0: P 0 Для состояния S1: P 1 ( Или, с учетом уравнения (3.10), для состояния S1 окончательно: P 1 Очевидно, для состояния S2 получим: P 2 Из уравнения для состояния S0 выразим P1 через P0:
C учетом (3.11), получим для вероятности Р2:
С учетом (3.12), для Р3:
И вообще, для любого k (от 1 до n)
Таким образом, все вероятности состояний выражаются через P0 . Подставив эти выражения в нормировочное условие (3.4) и вынеся P0 за скобку, получим:
Полученные формулы очень полезны при решении простейших задач теории массового обслуживания.
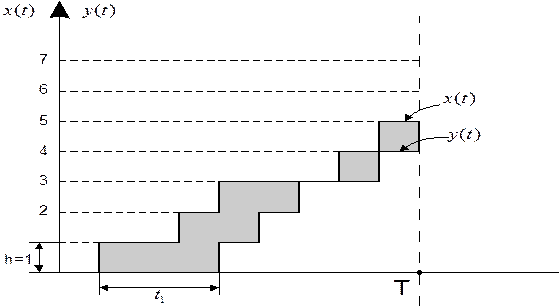
Формула Литтла Теперь выведем одну важную формулу, связывающую среднее число заявок Lсист, находящихся в системе массового обслуживания, и среднее время пребывания заявки в системе Wсист. Рассмотрим любую СМО и связанные с нею два потока событий: X(t) – число заявок, прибывших в СМО до момента t; Y(t) – число заявок, покинувших СМО до момента t. И та, и другая функции являются случайными и меняются скачком (увеличиваются на единицу в моменты приходов и уходов заявок). Вид функции X(t) и Y(t) показан на рисунке 3.6; обе линии - ступенчатые, верхняя – X(t), нижняя – Y(t). Очевидно, что для любого момента t их разность Z(t)=X(t)-Y(t) есть не что иное, как число заявок, находящихся в СМО. Когда линии X(t) и Y(t) сливаются, в системе нет заявок.
Рисунок 3.6 – К выводу формулы Литтла
Рассмотрим очень большой промежуток времени Т и вычислим для него среднее число заявок, находящихся в СМО. Оно будет равно интегралу от функции Z(t) на этом промежутке, деленному на длину интервала Т: Интеграл
где сумма распространяется на все заявки, пришедшие за время Т. Разделим правую и левую часть (3.17) на длину интервала Т, получим с учетом (3.16):
Разделим и умножим правую часть (3.18) на интенсивность
Но величина
откуда
Это и есть замечательная формула Литтла: для любой СМО, при любом характере потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания среднее время пребывания заявки в системе равно среднему числу заявок в системе, деленному на интенсивность потока заявок. Точно таким же образом выводим вторую формулу Литтла, связывающую среднее время пребывания заявки в очереди Wоч и среднее число заявок в очереди Lоч:
|
||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 154; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.007 с.) |

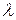 1= P 1
1= P 1 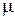 1 (3.10)
1 (3.10)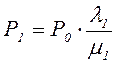 (3.11)
(3.11)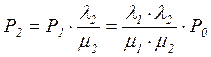 (3.12)
(3.12)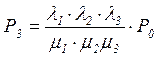 (3.13)
(3.13)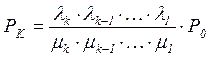 (3.14)
(3.14)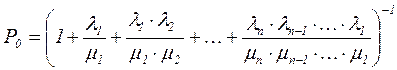 (3.15)
(3.15)
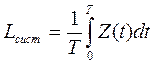
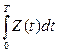 представляет собой не что иное, как площадь фигуры, заштрихованной на рисунке 3.6, состоящей из прямоугольников высотой, равной единице и основанием ti. Поэтому, можно считать, что
представляет собой не что иное, как площадь фигуры, заштрихованной на рисунке 3.6, состоящей из прямоугольников высотой, равной единице и основанием ti. Поэтому, можно считать, что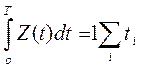 , (3.17)
, (3.17)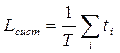 (3.18)
(3.18)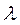 :
: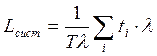 (3.19)
(3.19)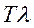 есть не что иное, как среднее число заявок, пришедших за время Т. Если мы разделим сумму всех времен ti на среднее число заявок, то получим среднее время пребывания заявки в системе Wсист. Итак,
есть не что иное, как среднее число заявок, пришедших за время Т. Если мы разделим сумму всех времен ti на среднее число заявок, то получим среднее время пребывания заявки в системе Wсист. Итак,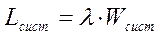 ,
,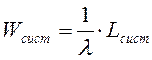 (3.20)
(3.20)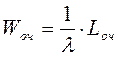 (3.21)
(3.21)


