Методы управления ресурсами многопроцессорных систем при обработке пакетов задач с прерываниями

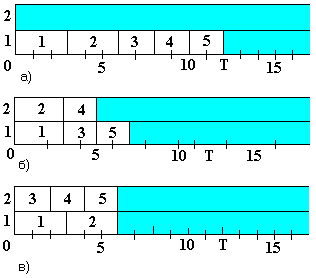
Алгоритм Макнотона

Рассмотрим систему с n идентичными процессорами, на которой необходимо решить L независимых задач; каждая задача решается одним процессором в течение времени t _i, i = 1,..., L. Требуется найти алгоритм, который для каждого данного пакета (набора) строил бы расписание решения задач на процессорах системы, обеспечивающее минимально возможное время решения. При этом достигается максимально возможная производительность системы. Например, в случае 2-процессорной системы и набора задач с временами (3,3,2,2,2) возможны различные варианты назначения задач на решение. Приведем некоторые из них (рисунок 3.13).

Рисунок 3.13 – Варианты расписаний решения задач

 

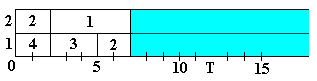
Очевидно, что наилучший в смысле минимизации общего времени решения задач - вариант в), для которого время Т решения пакета задач совпадает с соответствующим оптимальным значением Т₀и в данном случае равно величине

 = max { max t_i, 1/n * S t_i }

Величина  является нижней границей для оптимального значения Т₀. Действительно, длина Т любого расписания не может быть меньше ни max t _i  - максимального из времен решения задач пакета П, ни величины (1/n *  t_i), дающей длину расписания в том случае, когда до момента завершения решения последней из задач пакета ни один процессор не простаивает, то есть все процессоры имеют 100% загруженности.

В общем случае даже при n = 2 задача поиска оптимального значения Т при условии решения задач, является NP-трудной, то есть все известные алгоритмы ее решения имеют трудоемкость, экспоненциально зависящую от L. Однако, если допустить возможность прерывания решения задач пакета до завершения их обслуживания, то могут быть предложены полиномиально-трудоемкие алгоритмы, приводящие к расписанию оптимальной длины Т ₀. При этом считается, что после прерывания решение задачи может быть возобновлено с точки прерывания на любом процессоре, не обязательно на том, на котором она первоначально решалась. Число прерываний должно быть по возможности меньшим, так как с каждым актом прерывания связаны потери машинного времени на загрузку-выгрузку задач из оперативной памяти.

Рассмотрим предложенный Макнотоном в 1959 г. алгоритм построения оптимального по длине расписания с не более чем n-1 прерываниями.

Алгоритм Макнотона заключается в предварительном упорядочении задач по убыванию времени решения и назначении задач последовательно по порядку номеров одну за другой на процессоры системы справа налево от уровня .

Пример

n=2,L=4, времена решения задач:(5,4,3,2). Тогда

q = max {5, 1/2 *(5+4+3+2) } =7.

И расписание, полученное в соответствии с алгоритмом Макнотона, имеет следующий вид (рисунок 3.14):

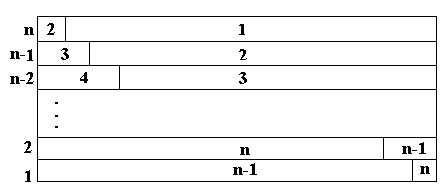
Рисунок 3.14

В данном случае число прерываний равно единице.

Покажем, что n - 1 (максимальное число прерываний для расписания, полученного в соответствии с алгоритмом Макнотона) является достижимой границей числа прерываний.

Для доказательства этого построим такой пример пакета задач, для которого алгоритм Макнотона дает расписание с числом прерываний n-1.

Пусть L = n +1 и t _i = n, i= 1,…, n+1.

Тогда  = max { n, 1/n * (n+1)*n = n+1, а расписание, получаемое в соответствии с алгоритмом Макнотона, имеет вид (рисунок 3.15):

Рисунок 3.15 – Расписание по алгоритму Макнотона

 

T=n+ 1 = q

Число прерываний в этом случае, как видно, равно
n - 1, что и требовалось показать. Покажем теперь, что любое оптимальное расписание для этого пакета задач также имеет не менее n - 1 прерываний. Очевидно, что в любом оптимальном расписании ни один процессор не простаивает на интервале [ 0,n+1 ]. Предположим, что существует некоторое оптимальное расписание с числом прерываний, меньшим n-1. Тогда по крайней мере 2 процессора (предположим для определенности P _k и P _l) обслуживают заявки без прерываний. Очевидно эти процессоры обслуживают некоторые задачи Z _ik и Z _il в интервале [0,n] без прерываний (если решение этих задач начинается позже момента времени t=0, значит до этого момента на этих процессорах решались некоторые другие задачи, решение которых прерывается в моменты начала решения задач Z _ik и Z _il). Найдутся моменты времени t, t`, такие, что
n  t < t`  n+1, и в интервале [ t, t` ] хотя бы один процессор простаивает, а потому рассматриваемое решение не может быть оптимальным.

Так как мы пришли к противоречию, делаем вывод о том, что предположение о числе прерываний, меньшем n-1, в оптимальном расписании ложно.