
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие Марковского случайного процессаСодержание книги
Поиск на нашем сайте
Случайный процесс, протекающий в системе, называется марковским, если для любого момента времени tо вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент tо и не зависят от того, когда и как система пришла в это состояние [4]. Пусть в настоящий момент tо система находится в определенном состоянии Sо (см. рисунок 3.1)
Рисунок 3.1 – К понятию Марковского случайного процесса
Мы наблюдаем процесс со стороны и в момент tо знаем состояние системы Sо и всю предысторию процесса, все, что было при t<tо. Нас интересует будущее(t>to). В точности предсказать его мы не можем, так как процесс случайный. Но мы можем найти некоторые вероятностные характеристики процесса в будущем, например, вероятность того, что через некоторое время t система S окажется в состоянии S1 или сохранит состояние So, и т.п. Таким образом, если процесс марковский, то предсказывать можно, только учитывая настоящее состояние системы So и забыв о его предыстории. Само состояние So зависит от прошлого, но как только оно достигнуто, о прошлом можно забыть. Иначе формулируя, в марковском процессе «будущее зависит от прошлого только через настоящее». На практике марковские процессы в чистом виде обычно не встречаются, но нередко приходится иметь дело с процессами, для которых влиянием предыстории можно пренебречь. При их изучении можно с успехом применять марковские модели. В исследовании операций большое значение имеют так называемые марковские процессы с дискретным состоянием и непрерывным временем. Процесс называется процессом с непрерывным временем, если моменты возможных переходов из состояния в состояние не фиксированы заранее, а неопределенны, случайны, если переход может осуществиться, в принципе, в любой момент.
Потоки событий Потоком событий называется последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени. Например, поток вызовов на телефонной станции; поток сбоев ЭВМ. Поток событий можно наглядно изобразить рядом точек на оси времени 0t, причем положение их случайно (см. рисунок 3.2).
Рисунок 3.2 - Поток событий
Важной характеристикой потока событий является его интенсивность Поток событий называется простейшим (или стационарным пуассоновским), если он обладает сразу тремя свойствами: стационарен, ординарен и без последействия. Название Для простейшего потока с интенсивностью
с плотностью
Рисунок 3.3 - Показательное распределение
Величина T £ 1 / то такой интервал называют коротким. Для простейшего потока характерно, что короткие интервалы между событиями более вероятны, чем длинные; ≈ 63 % промежутков времени между событиями имеют длину меньше средней, равной 1/ λ. Таким образом, предположение о действии на вычислительную систему простейшего потока заявок создает более тяжелые условия для ее работы, чем при других потоках, что позволяет считать результаты анализа ВС для простейших потоков заявок более надежными. В расчетах, связанных с потоками событий, очень удобно пользоваться понятием «элемента вероятности». Рассмотрим на оси Ot простейший поток с интенсивностью P D t = то есть для простейшего потока элемент вероятности равен интенсивности потока, умноженной на длину элементарного участка. Элемент вероятности из-за отсутствия последействия, совершенно не зависит от того, сколько событий и когда появлялись ранее.
Уравнения Колмогорова
Пусть техническое устройство S состоит из двух узлов, каждый из которых в случайный момент времени может выйти из строя, после чего мгновенно начинается ремонт узла, тоже продолжающийся заранее неизвестное, случайное время. Возможные состояния системы можно перечислить: S0 – оба узла исправны; S1 - первый узел ремонтируется, второй исправен; S2 - второй узел ремонтируется, первый исправен; S3 – оба узла ремонтируются. Переходы системы из состояния в состояние происходят практически мгновенно, в случайные моменты выхода из строя того или другого узла или окончания ремонта. При анализе случайных процессов с дискретными состояниями удобно пользоваться графом состояний, в котором состояния системы изображаются окружностями, а возможные переходы из состояние в состояние – стрелками, соединяющими состояния. Граф состояний для рассмотренного выше примера изображен на рисунке 3.4
Рисунок 3.4 - Граф состояний
Стрелка, направленная из S0 в S1, означает переход в момент отказа первого узла; стрелка, направленная обратно, из S1 в S0 - переход в момент окончания ремонта этого узла. Остальные стрелки объясняются аналогично. Буквой Вероятностью i-го состояния называется вероятность Pi(t) того, что в момент t система будет находиться в состоянии Si. Очевидно, что для любого момента сумма всех вероятностей состояний равна единице:
Имея в своем распоряжении размеченный граф состояний, можно найти все вероятности состояний Pi(t) как функции времени. Для этого составляются и решаются так называемые уравнения Колмогорова - особого вида дифференциальные уравнения, в которых неизвестными функциями являются вероятности состояний. Составим эти уравнения для заданной системы. Рассмотрим одну из вероятностей состояний, например P0(t). Это вероятность того, что в момент t система будет в состоянии S0 . Придадим t малое приращение Δt и найдем P0(t+Δt) – вероятность того, что в момент (t+Δt) система будет в состоянии S0. Произойти это может тремя способами: либо в момент t система уже была в состоянии S0, а за время Δt не вышла из него; либо в момент t система была в состоянии S1, а за время Δt перешла из него в S0; либо в момент t система была в состоянии S2, а за время Δt перешла из него в S0. Найдем вероятность первого варианта. Вероятность того, что в момент t система была в состоянии S0 , равна P0(t). Эту вероятность нужно умножить на вероятность того, что, находившись в момент t в состоянии S0, система за время Δt не перейдет из него в другое состояние. Суммарный поток событий, выводящий систему из состояния S0, будет простейший, с интенсивностью ( Значит, вероятность того, что за время Δt система выйдет из состояния S0, равна ( Вероятность второго варианта равна ( Складывая вероятности всех вариантов, получим: P0(t+Δt)= P0(t)* [1-( Раскроем квадратные скобки, перенесем P0(t) в левую часть и разделим обе части на Δt:
Устремив Δt к нулю, получим:
Таким образом, мы получили первое уравнение Колмогорова. Аналогично составляются и следующие уравнения. Сформулируем теперь общее правило составления уравнений Колмогорова. В левой части каждого из них стоит производная вероятности данного состояния. В правой части – сумма произведений вероятностей всех состояний, из которых идут стрелки в данное состояние, на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводяших систему из данного состояния, умноженная на вероятность данного состояния. Пользуясь этим правилом, получим уравнения Колмогорова для рассмотренной системы S:
Чтобы решить эти уравнения и найти вероятности состояний, необходимо задать начальные условия. Правомерен вопрос: что будет происходить с вероятностями состояний при t, стремящемся к бесконечности? Будут ли Pi(t) стремиться к каким-то пределам? Если эти пределы существуют и не зависят от начального состояния системы, то они называются финальными вероятностями состояний. Если вероятности Pi(t) постоянны, то их производные равны нулю. Значит, чтобы найти финальные вероятности, нужно все левые части в уравнениях Колмогорова положить равными нулю и решить полученную систему уже не дифференциальных, а линейных алгебраических уравнений. Для нашей системы они будут выглядеть следующим образом: P 0 * ( P 1 * ( P 2 * ( P 3 * ( Для решения этой системы необходимо воспользоваться нормировочным условием P 0+ P 1+ P 2+ P 3 = 1.
|
||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 138; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.18.192 (0.006 с.) |

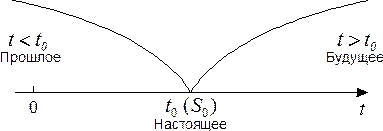
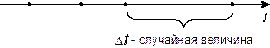
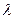 – среднее число событий, приходящееся на единицу времени. Интенсивность может быть как постоянной, так и переменной, зависящей от времени t.
– среднее число событий, приходящееся на единицу времени. Интенсивность может быть как постоянной, так и переменной, зависящей от времени t. простейший связано с тем, что процессы, связанные с простейшими потоками, имеют наиболее простое математическое описание.
простейший связано с тем, что процессы, связанные с простейшими потоками, имеют наиболее простое математическое описание.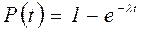
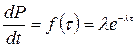 (τ>0) (3.1)
(τ>0) (3.1)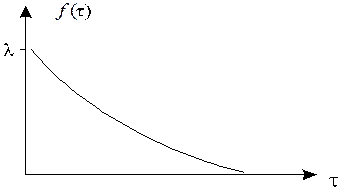
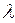 , (3.2)
, (3.2)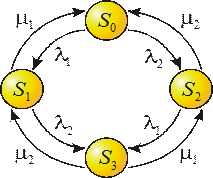
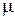 i обозначена интенсивность ремонта i-го узла.
i обозначена интенсивность ремонта i-го узла.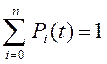 (3.4)
(3.4)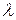 1+
1+ 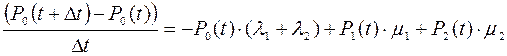 (3.6)
(3.6)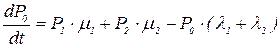 (3.7)
(3.7) (3.8)
(3.8)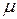 1+ P 2 *
1+ P 2 * 


