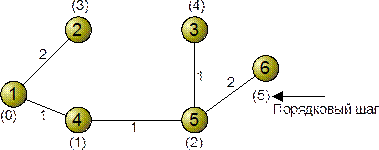Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сети с коммутацией сообщенийСодержание книги
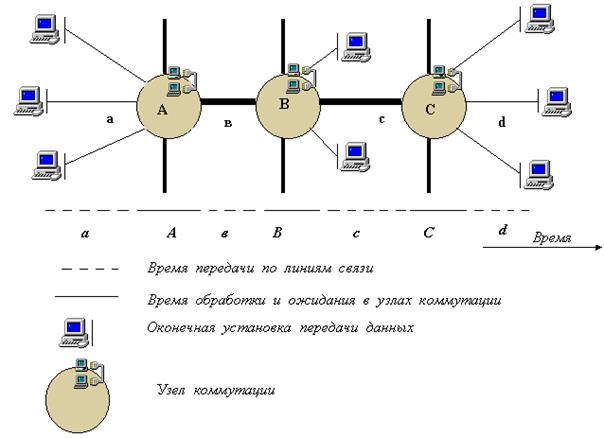
Поиск на нашем сайте В сети с коммутацией сообщений между оконечными установками, обменивающимися информацией, нет сквозного соединения. В коммутационных узлах сообщения заносятся в память и передаются далее по участкам переприёма от узла к узлу. На рисунке 4.39 показана схема сети с коммутацией сообщений. На оконечной установке, от которой необходимо передать сообщение, оно снабжает заголовком, содержащим адрес желаемого абонента, и по абонентской линии а передается на ближайший коммутационный узел А. В нем сообщение запоминается, обрабатывается его заголовок, определяется в какую из исходящих линий далее его нужно направить и, наконец, передаётся на следующий коммутационный узел В.
Рисунок 4.39-Сеть с коммутацией сообщений
Если линия в, по которой нужно передать сообщение далее, занята, то оно остаётся в запоминающем устройстве (буферном накопителе узла) до тех пор, пока не будут переданы все находящиеся перед ним в очереди другие сообщения. Поскольку на участке в магистральном канале скорость передачи обычно выше, чем в абонентской линии а, длительность передачи по этому участку на временной диаграмме (см. рисунок 4.38) показана более короткой. Узел коммутации В, в котором сообщение обрабатывается так же, как и в узле А, передает сообщение по линии с на узел С. От последнего оно передается по абонентской линии d на принимающий модуль абонента. Время ожидания, в течение которого сообщение хранится в узле коммутации, зависит от длины очередей на линии связи, поэтому общее время прохождения сообщения между двумя оконечными установками в сети может быть различным. Запись сообщений в память упрощает трансформацию скоростей различного оборудования данных, осуществляемую в коммутационных узлах. Использование на межузловых участках дуплексных высокоскоростных линий связи позволяет более эффективно, чем в сетях с коммутацией каналов, передавать требуемый объём информации и использовать ресурсы сети. Однако экономию линий связи необходимо сопоставлять с затратами, которых требуют запоминание и обработка сообщений в узлах коммутации.
Сеть с пакетной коммутацией Коммутация пакетов является развитием метода коммутации сообщений. Она позволяет добиться дальнейшего увеличения пропускной способности сети, скорости и надежности передачи данных. В сети с коммутацией пакетов сообщения разделяются на отдельные части, называемые пакетами (см. рисунок 4.39).
Рисунок 4.40-Пакетирование сообщений
В принимающем коммутационном узле каждый пакет проверяется на наличие ошибок. На пакеты, принятые без ошибок, в ответ направляется подтверждение их приёма (положительная квитанция ДА). Если же в пакете обнаружены ошибки, то посылается запрос на его повторную передачу (отрицательная квитанция НЕТ). Для передачи отдельных пакетов каждого сообщения по сети могут выбираться различные пути (рисунок 4.41), что обеспечивает более гибкое и оперативное приспособление к состояниям занятости тех или иных линий связи и узлов коммутации. При этом могут возникнуть ситуации, при которых пакеты могут поступать в адрес получателя в неверной последовательности.
Рисунок 4.41-Различные пути передачи пакетов
Известны два способа передачи пакетов в сети передачи данных: виртуальный и датаграммный. При работе в режиме виртуального канала коммутационный узел пункта назначения сортирует поступившие на него пакеты перед их дальнейшей передачей на оконечную станцию. В датаграммном режиме передачи сортировка возлагается на принимающую оконечную станцию. Метод коммутации пакетов по сравнению с другими методами обеспечивает наименьшую задержку при передаче данных и наибольшую пропускную способность сети. Управление потоком в сети На сетевом уровне, в отличии от канального, в котором управление идет между двумя точками, должно быть организовано управление потоком по всему виртуальному каналу от источника до получателя. При этом предполагается, что канальный уровень справляется со своими задачами и ошибок в передаче между узлами нет. Если в сеть поступает большое число пакетов, то заметно растут задержки; производительность, измеряемая числом пакетов, доставляемых по назначению в единицу времени, начинает снижаться. Если поступающая нагрузка достаточно высока, может даже возникнуть тупиковая ситуация, когда все накопители оказываются переполнены, поступление нагрузки прекращается и производительность падает до нуля. Для предотвращения возникновения тупиковых ситуаций существуют специальные методы. Наиболее распространенным является метод скользящего окна [11].
Метод скользящего окна Окно – это неподтвержденные пакеты, находящиеся в виртуальном канале. Рассмотрим виртуальный канал (ВК), проходящий на пути от источника к получателю по сети с коммутацией пакетов М узлов с накоплением и воспроизведением информации. Он представлен в виде разомкнутой сети массового обслуживания (см. рисунок 4.42).
Рисунок 4.42-Модель массового обслуживания
Если предположить, что каждая система независима, то можно применить аппарат теории массового обслуживания.
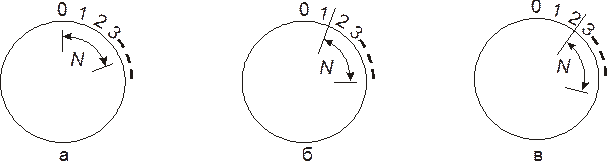
Рисунок 4.43-Управление с помощью скользящего окна: (а) начальное состояние, (б) пакет 1 подтвержден, (в) следующий пакет (2) подтвержден
Разомкнутая сеть может быть отнесена к составным системам массового обслуживания. Она имеет показатели, определенные в форме произведения (то есть вероятности состояний всей сети выражаются произведениями вероятностей состояний каждой системы обслуживания). Наложим на эту модель скользящее окно (рисунок 4.44).
Рисунок 4.44-Модель управления с помощью скользящего окна
В данном случае – частный случай замкнутой сети массового обслуживания. Здесь источник и получатель связаны дополнительной искусственной системой обслуживания, обозначаемой М+1, интенсивность обслуживания которой равна Теорема Нортона: в сети массового обслуживания любой участок сети, содержащий несколько узлов, может быть заменен одним эквивалентным узлом, производительность которого зависит от состояния преобразуемого участка сети. Теорема устанавливает, что М последовательных систем обслуживания между точками И и П могут быть заменены одной системой обслуживания, зависящей от состояния, без изменения статистических характеристик между точками И и П. На рисунке 4.45 показана замкнутая сеть массового обслуживания с одной системой обслуживания СО, вынесенной за ее пределы. Предположим, что требуется найти вероятности состояний только этой системы. Теорема Нортона устанавливает, что если сеть массового обслуживания имеет решение в форме произведения, то отдельная зависящая от состояния система массового обслуживания, входящая в эту сеть, может быть выделена путем короткого замыкания точек А и В, как показано на рисунке 4.45б, позволяя n пакетам циркулировать по вновь образованной замкнутой сети. Значительно более простой эквивалентной моделью для решения этой задачи является модель, показанная на рисунке 4.45в. В ней эквивалентная система обслуживания Нортона с интенсивностью обслуживания u(n), где n – состояние СО, заменяет всю сеть между точками А и В на рисунке 4.45а.
а) б)
в)
Рисунок 4.45-Применение теоремы Нортона к сетям массового обслуживания: (а) исходная сеть, (б) применение теоремы Нортона, (в) эквивалентная модель
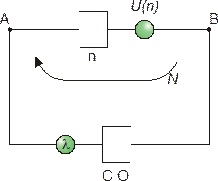
Пусть теперь общее количество пакетов равно N. Если верхняя система обслуживания находится в состоянии n, то нижняя система будет в состоянии N-n. Вероятность pn того, что верхняя система находится в состоянии n равна
где р0 находится из обычного нормирующего условия для вероятностей
Эквивалентная замена для рассматриваемой сети приводит к зависящей от состояния характеристике обслуживания
Производительность u(n) в случае, когда среди М показанных СО распределены n пакетов, всегда меньше или равна
Производительность
На основании формулы Литтла задержка Е(Т) ВК из конца в конец равна отношению среднего числа пакетов в ВК к
Чтобы увидеть, как хорошо работает управление с помощью окна и определить значение N, предлагаемое для соответствующей характеристики управления, рассмотрим область очень большой нагрузки. Предположим, что
На основании формулы Литтла непосредственно получим
Из этого равенства видно, что минимальная задержка
Равенство справедливо только для целых значений N. Какое значение N должно применяться? Из (4.21) и (4.22) видно, что оптимальное N = M-1. Увеличение N за пределы этой точки приводит к устойчивому росту задержки.
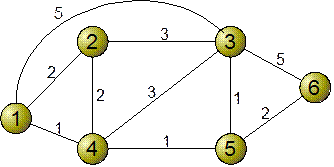
Выбор кратчайших путей 4.6.3.1.Алгоритм Дейкстры Рассмотрим сеть на рисунке 4.46. Числа, проставленные у каждой линии, указывают ее стоимость. Целью является нахождение кратчайшего пути от узла 1, являющегося источником, ко всем остальным узлам сети.
Рисунок 4.46-Пример сети
Обозначим через D(v) расстояние от источника 1 до узла v. Пусть L(i, j) - заданная стоимость пути между узлами i и j. Алгоритм состоит из двух частей: начального шага и итераций, повторяющихся до завершения алгоритма. В множество N будем заносить кратчайшие пути к узлам. 1. Начальный шаг Устанавливаем N = {1}. Для каждого узла v, не принадлежащего множеству N, устанавливаем D(v) = L(1,v). (Расстояние до узлов, не соединенных с узлом 1, принимаем равным бесконечности). 2. Каждый последующий шаг. Находим не принадлежащий множеству N узел w, для которого D(w) минимально и включаем w в множество N. Затем обновляем значения D(w) для всех остальных узлов, не принадлежащих N путем вычисления D(v) Шаг 2 повторяется, пока в множество N не войдут все узлы. Применение этого алгоритма к сети иллюстрируется последовательными шагами, указанными в таблице 4.3. Полужирным курсивом в столбцах обозначены минимальные значения D(w) на каждом шаге (при равных расстояниях выбор производится случайным образом). После каждого шага соответствующий узел w добавляется к N. Затем величины D(v) обновляются. Например, после начального шага во время шага 1 к множеству N добавляется узел 4, имеющий минимальное значение D(4)=1. На шаге 2 в N включается узел 5 при D(5)=2, и т.д. После шага 5 все узлы оказываются включенными в множество N и алгоритм завершается.
Таблица 4.3 Применение алгоритма Дейкстры к сети рисунка 4.46
По мере работы алгоритма, приводящей к результатам, показанным в таблице, в то же самое время строится дерево кратчайших путей с корнем в узле 1: при включении узла во множество N он соединяется с соответствующим узлом, уже принадлежащим N. Результирующее дерево для сети показано на рисунке 4.47. Цифры в скобках у каждого узла указывают шаг, на котором этот узел был включен в дерево. С помощью дерева кратчайших путей для узла 1 можно получить таблицу маршрутов для узла 1, показывающую исходящий путь, по которому нужно направлять пакеты к узлу назначения. Подобная таблица маршрутов может быть составлена для каждого узла, являющегося источником сообщений.
а)
б) Рисунок 4.47-Применение алгоритма Дейкстры к рисунку 4.46. Источник - узел 1: а) - построение дерева, б) - таблица маршрутов. Алгоритм Флойда Он также состоит из двух частей: начального шага и расчетов кратчайших расстояний, которые повторяются до завершения алгоритма. Здесь кратчайшее расстояние представляет собой расстояние до данного узла от узла 1, например, рассматриваемого как узел назначения. Алгоритм заканчивается, когда для всех узлов фиксируется их расстояние до узла 1 (узла получателя) и отмечаются следующие узлы по направлению к узлу назначения по кратчайшему пути. Построение таблицы маршрутов требует повторного или параллельного применения этого алгоритма для каждого узла назначения, что дает в результате набор меток для каждого узла, причем каждая метка дает информацию о маршруте и расстоянии до конкретного узла назначения. Рассмотрим опять рисунок 4.46. Обращаясь ко второй части алгоритма и применяя ее в циклическом порядке для узлов 2-6, находим, что алгоритм завершается после двух циклов. Эти циклы и полученные в результате метки каждого цикла, приводятся в таблице 4.4 (любой другой порядок обхода узлов приводит к тому же самому окончательному результату).
Таблица 4.4 Применение алгоритма Флойда к сети рисунка 4.45
Таким образом, в цикле 1 нужно отметить, что узел 2 является «ближайшим» к его соседу 1. Его результирующая новая стоимость равна D(v)=D(1)+L(1,2)=2. Следовательно, метка, как это и указано, имеет вид (1,2). Переходя к узлу 3, приходим к необходимости выбора стоимостей между D(2)+L(2,3)=5 или D(1)+L(1,3)=5. Выбирая произвольно D(1)+L(1,3), получим (1,5), что показано в таблице (при другом выборе получится то же самое). Аналогично получаются другие результаты. В цикле 2 узел 3 имеет теперь пять соседних узлов с конечными значениями D(w), между которыми нужно произвести выбор. Минимальное значение D(w)+L(w,3) равно D(5)+L(5,3), и метка узла 3, как показано, меняется на (5,3). Другие узлы не меняют своих меток, и алгоритм завершается. Опять же дерево кратчайших путей с корнем в узле 1, как показано на рисунке2а, может быть получено путем обхода меток каждого узла. В результате, узел 2 соединяется с узлом 1, узел 3 - с узлом 5, узел 4 - с узлом 1, узел 5 - с узлом 4 и узел 6 - с узлом 5. Иначе, таблица маршрутов или значение следующего узла в каждом узле по направлению к узлу 1 в точности является первым числом каждой двузначной метки, что и указывалось выше. Для получения полной таблицы маршрутов в каждом узле алгоритм должен быть повторен для каждого узла, принимаемого в качестве узла назначения.
Глобальная сеть INTERNET В настоящее время существует два созвучных термина – internet и Internet. Под internet понимают технологию обмена данными, основанную на использовании протоколов TCP/IP, а под Internet – глобальное сообщество мировых сетей, которые используют internet для обмена данными. Internet начинался, аналогично большинству современных технологий, как военная программа, направленная на повышение устойчивости системы обороны США.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 398; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.015 с.) |

 Каждый пакет имеет, как правило, фиксированную длину и снабжается заголовком, указывающим адрес пункта отправления, адрес пункта назначения и номер пакета в сообщении. Максимальная длина пакета лежит в пределах от 104 до 2*104 бит. Разложение сообщения на пакеты и восстановление его после передачи осуществляются оконечным оборудованием источника и адресата.
Каждый пакет имеет, как правило, фиксированную длину и снабжается заголовком, указывающим адрес пункта отправления, адрес пункта назначения и номер пакета в сообщении. Максимальная длина пакета лежит в пределах от 104 до 2*104 бит. Разложение сообщения на пакеты и восстановление его после передачи осуществляются оконечным оборудованием источника и адресата.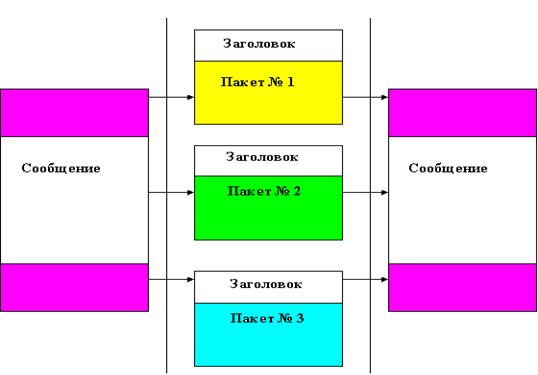



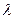 , что соответствует интенсивности входящего потока в ВК. По замкнутой системе циркулирует фиксированное число N пакетов. Отметим теперь, как эта модель замкнутой системы охватывает механизм скользящего окна. Если в ВК (верхние М систем обслуживания) находятся N пакетов, нижняя система обслуживания М+1 пуста и обслуживать не может. Это моделирует состояние блокировки, которое пакеты встречают при поступлении в момент исчерпанного окна. В момент, когда один из N пакетов в ВК поступает к получателю, он появляется в системе обслуживания М+1 и источник теперь может доставить пакеты с пуассоновской интенсивностью
, что соответствует интенсивности входящего потока в ВК. По замкнутой системе циркулирует фиксированное число N пакетов. Отметим теперь, как эта модель замкнутой системы охватывает механизм скользящего окна. Если в ВК (верхние М систем обслуживания) находятся N пакетов, нижняя система обслуживания М+1 пуста и обслуживать не может. Это моделирует состояние блокировки, которое пакеты встречают при поступлении в момент исчерпанного окна. В момент, когда один из N пакетов в ВК поступает к получателю, он появляется в системе обслуживания М+1 и источник теперь может доставить пакеты с пуассоновской интенсивностью 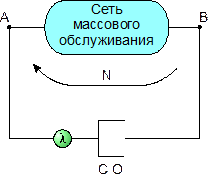

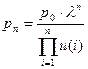 (4.15)
(4.15)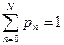 (4.16)
(4.16)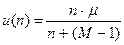 . (4.17)
. (4.17)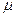 . Она должна удовлетворять условию
. Она должна удовлетворять условию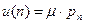 {система непуста}. (4.18)
{система непуста}. (4.18)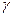 ВК, управляемого с помощью окна, получается усреднением интенсивностей обслуживания по всем N:
ВК, управляемого с помощью окна, получается усреднением интенсивностей обслуживания по всем N: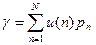
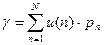 . (4.19)
. (4.19)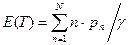 . (4.20)
. (4.20)
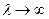 . Тогда очевидно, что как только пакет поступит к получателю и к источнику вернется подтверждение, в ВК немедленно вводится другой пакет. Таким образом, в этом предельном случае ВК всегда находится в состоянии N, E(n)=N и производительность
. Тогда очевидно, что как только пакет поступит к получателю и к источнику вернется подтверждение, в ВК немедленно вводится другой пакет. Таким образом, в этом предельном случае ВК всегда находится в состоянии N, E(n)=N и производительность 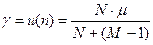 ,
, 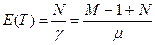 ,
, 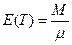 имеет место при N=1. Это соответствует ожиданию. При увеличении размера окна N задержка растет пропорционально, а производительность сначала линейно растет с N, но затем выравнивается, приближаясь к максимальному значению
имеет место при N=1. Это соответствует ожиданию. При увеличении размера окна N задержка растет пропорционально, а производительность сначала линейно растет с N, но затем выравнивается, приближаясь к максимальному значению 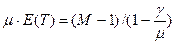 ,
, 
 min[D(v), D(w)+L(w,v)]/ (4.24)
min[D(v), D(w)+L(w,v)]/ (4.24)