
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уменьшения высоты дерева арифметического выраженияСодержание книги
Поиск на нашем сайте
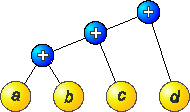
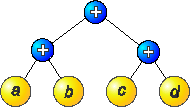
На рисунке 2.2 показаны деревья разбора для арифметического выражения (((a+b)+c)+d). На рисунке 2.2а изображено дерево минимальной высоты (h = 3) для первоначального выражения, а на рисунке 2.2б - дерево, высота которого уменьшена до двух уровней (h = 2) путем преобразования первоначального выражения к виду (a+b)+(c+d) с использованием ассоциативности. Для арифметического выражения с n переменными или константами уменьшение высоты дерева позволяет достигнуть ускорения обработки порядка
а) б) Рисунок 2.2 – Деревья разбора Замена операторов Рассмотрим следующий блок операторов присваивания: X=BCD+E Y=AX Z=X+FG При использовании одного процессора этот блок может быть вычислен за шесть шагов, если один временной шаг отводится для каждой арифметической операции. Путем замены операторов можно получить следующий блок: X=BCD+E Y=ABCD+AE Z=BCD+E+FG Этот блок может быть вычислен параллельно за три шага с ускорением обработки U = 6/3 = 2 при использовании 5 процессоров. Приведенные примеры преобразований показывают, какое ускорение можно получить, используя параллельную обработку и оптимизацию выражений.
Конвейерная обработка Конвейерная обработка улучшает использование ресурсов для заданного набора процессов, каждый из которых применяет эти ресурсы заранее предусмотренным способом. Хорошим примером конвейерной организации является сборочный транспортер на производстве, на котором изделие последовательно проходит все стадии вплоть до готового продукта. Преимущество этого способа состоит в том, что все изделия вдоль своего пути используют один и тот же набор ресурсов, и как только некоторый ресурс освобождается данным изделием, он сразу же может быть использован следующим изделием, не ожидая, пока предыдущее изделие достигнет конца сборочной линии. Если транспортер несет аналогичные, но не тождественные изделия, то это – последовательный конвейер; если же все изделия одинаковы, то это – векторный конвейер. Последовательные конвейеры Разработчики компьютеров издавна прибегали к методам проектирования, известным под общим названием "совмещение операций", при котором аппаратура компьютера в любой момент времени выполняет одновременно более одной базовой операции. Этот общий метод включает два понятия: параллелизм и конвейеризацию. При параллелизме совмещение операций достигается путем воспроизведения в нескольких копиях аппаратной структуры. Высокая производительность достигается за счет одновременной работы всех элементов структур, осуществляющих решение различных частей задачи. Конвейеризация (или конвейерная обработка) в общем случае основана на разделении подлежащей исполнению функции на более мелкие части, называемые ступенями, и выделении для каждой из них отдельного блока аппаратуры. Так обработку любой машинной команды можно разделить на несколько этапов (несколько ступеней), организовав передачу данных от одного этапа к следующему. При этом конвейерную обработку можно использовать для совмещения этапов выполнения разных команд. Производительность при этом возрастает благодаря тому, что одновременно на различных ступенях конвейера выполняются несколько команд. Конвейерная обработка такого рода широко применяется во всех современных быстродействующих процессорах. На рисунке 2.3 показано устройство обработки команд простейшего процессора, которое включает четыре ступени: 1. выборка команд из памяти; 2. декодирование; 3. определение адреса и выборка операнда; 4. исполнение.
Рисунок 2.3 – Последовательный конвейер
Конвейеризация увеличивает пропускную способность процессора (количество команд, завершающихся в единицу времени), но она не сокращает время выполнения отдельной команды. В действительности, она даже несколько увеличивает время выполнения каждой команды из-за накладных расходов, связанных с хранением промежуточных результатов. Однако увеличение пропускной способности означает, что программа будет выполняться быстрее по сравнению с простой неконвейерной схемой.
Рисунок 2.4 – Диаграмма работы последовательного
Ускорение обработки в данном устройстве измеряется отношением времени Ts, необходимом для последовательного выполнения L заданий (без конвейеризации), ко времени Tp выполнения той же обработки на конвейере. Обозначим через ti время обработки на i-той ступени, а через tj - соответствующее время для самой медленной ступени (j? i). Тогда, если L заданий (команд) проходят через конвейер с n ступенями (для рисунков 2.3 и 2.4 – четыре ступени), эффективность конвейера определяется следующим выражением: для Как видно из этого анализа, первый результат на выходе конвейера появляется спустя время tраз = Конвейеризация эффективна только тогда, когда загрузка конвейера близка к полной, а скорость подачи новых команд и операндов соответствует максимальной производительности конвейера. Если произойдет задержка, то параллельно будет выполняться меньше операций и суммарная производительность снизится. Такие задержки могут возникать в результате появления конфликтных ситуаций. Конфликты снижают реальную производительность конвейера, которая могла бы быть достигнута в идеальном случае. Существуют три класса конфликтов: 1. Структурные конфликты, которые возникают из-за конфликтов по ресурсам, когда аппаратные средства не могут поддерживать все возможные комбинации команд в режиме одновременного выполнения с совмещением. 2. Конфликты по данным, возникающие в случае, когда выполнение одной команды зависит от результата выполнения предыдущей команды. 3. Конфликты по управлению, которые возникают при конвейеризации команд переходов и других команд, которые изменяют значение счетчика команд. Конфликты в конвейере приводят к необходимости приостановки выполнения команд (pipeline stall). Обычно в простейших конвейерах, если приостанавливается какая-либо команда, то все следующие за ней команды также приостанавливаются. Команды, предшествующие приостановленной, могут продолжать выполняться, но во время приостановки не выбирается ни одна новая команда. Векторные конвейеры В векторных машинах создается множество функциональных элементов, каждый из которых выполняет определенную операцию с парой операндов, принадлежащих двум разным векторам. Эти пары подаются на функциональное устройство (включающее множество одинаковых функциональных элементов) одновременно и со всеми парами элементов векторов проводят одновременно функциональные преобразования. Для предварительной подготовки преобразуемых векторов используются векторные регистры, на которые собираются подлежащие обработке вектора. Типичное использование векторного конвейера – это процесс, вырабатывающий по двум исходным векторам А и В результирующий вектор С для арифметической операции С = А + В. В этом случае на конвейер поступает множество одинаковых команд. Векторная команда в этом примере реализуется с помощью специального управляющего вектора. Если n -й разряд управляющего вектора установлен в 1, то операция Cn = Ап + Вп выполняется и С n записывается в результирующий вектор. Как видно из примера, по мере вычисления адресов пары операндов могут непрерывно вводиться в арифметическое устройство. В такой конвейерной архитектуре требуются регистры или управляющие векторы, хранящие необходимую информацию до тех пор, пока можно начать выполнение команды. Подготовка данных для векторной обработки может потребовать выполнения нескольких операций загрузки регистров. Необходимое для этого время называют временем подготовки ts. Время от момента декодирования векторной команды до появления на выходе конвейера первого элемента результирующего вектора называют временем разгона конвейера tf. Если длина обрабатываемого векторного поля равна l, а время обработки на самой медленной ступени равно tb, то общее время выполнения на конвейере векторной команды составляет
tvp = ts + tf +(l - 1) tb
Для того чтобы выполнить ту же обработку на последовательном конвейере, потребовалось бы использовать его l раз. По сравнению с векторными конвейерами выборка операндов на последовательных конвейерах реализуется менее эффективно. Эквивалентом оценки tvp в последовательном конвейере является величина
tsq = tfs +(l - 1 ) tbs где tsq, tfs и tbs — соответственно время обработки на последовательном конвейере, время его разгона и время обработки на самой медленной его ступени. Сравнивая tvp и tsq, получаем
ts + tf +(l - 1) tb £ tfs +(l - 1) tbs,
если справедливо соотношение
l ³ 1 + (ts + tf - tfs)/(tbs - tb)
Приведенные характеристики показывают, в каких случаях векторный конвейер имеет преимущества по сравнению с последовательным. В работе [6] установлено, что знаменатель, как правило, составляет около одной десятой числителя, что соответствует значению l ³ 10.
|
|||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 92; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.27.70 (0.197 с.) |


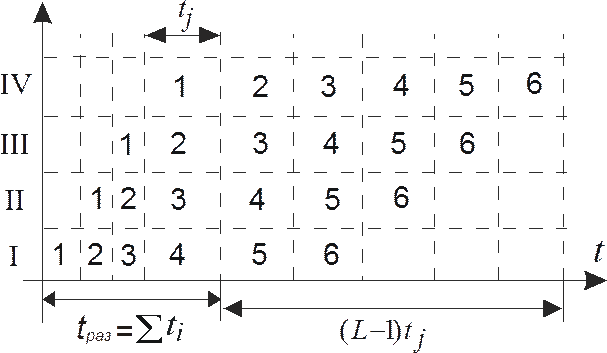
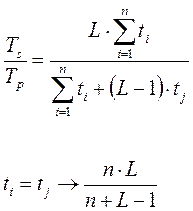 (4.3)
(4.3)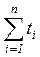 , называемое временем разгона конвейера, а последующие – с интервалами tj.
, называемое временем разгона конвейера, а последующие – с интервалами tj.


