
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Простейшие системы массового обслуживания и их характеристикиСодержание книги
Поиск на нашем сайте Все потоки событий, переводящие систему массового обслуживания (СМО) из состояния в состояние, будем считать простейшими. Поток обслуживаний - поток заявок, обслуживаемых одним непрерывно занятым каналом. В этом потоке интервал между событиями, как и всегда в простейшем потоке, имеет показательное распределение.
Задача Эрланга Рассмотрим одну из первых по времени «классических» задач теории массового обслуживания; эта задача возникла из практических нужд телефонии и была решена в начале нашего века датским математиком Эрлангом. Задача ставится так: имеется n каналов, на которые поступает поток заявок с интенсивностью l. Поток обслуживания одним каналом имеет интенсивность m (величина, обратная среднему времени обслуживания tob). Найти финальные вероятности состояний СМО, а также характеристики ее эффективности: А – абсолютную пропускную способность, то есть среднее число заявок, обслуживаемых в единицу времени; Q – относительную пропускную способность, то есть среднюю долю пришедших заявок, обслуживаемых системой; Ротк - вероятность отказа, то есть того, что заявка покинет СМО необслуженной;
Состояние системы массового обслуживания S будем нумеровать по числу заявок, находящихся в системе (в данном случае оно совпадает с числом занятых каналов): S0 – в СМО нет ни одной заявки; S1 - в СМО находится одна заявка (один канал занят, остальные свободны); ..... Sk - в СМО находится k заявок (k каналов заняты, остальные свободны) Sn - в СМО находятся n заявок (все n каналов заняты). Граф состояний СМО выглядит следующим образом (рисунок 3.7):
Рисунок 3.7 – Граф состояний многоканальной СМО
Разметим этот граф – проставим у стрелок интенсивности потоков событий. Интенсивности потоков l все одинаковы, что естественно, так как на СМО действует один и тот же внешний поток заявок на обслуживание. Интенсивности же потоков обслуживания увеличиваются с каждым занятым каналом. А теперь, зная все интенсивности, воспользуемся уже готовыми формулами для финальных вероятностей в системе гибели-размножения. Получим:
где! обозначает факториал. Члены разложения
Заметим, что в формулы (3.22), (3.23) интенсивности l и m входят не по отдельности, а только в виде отношения l / m. Обозначим
и будем называть величину
Формулы (3.25) для финальных вероятностей состояний называются формулами Эрланга - в честь основателя теории массового обслуживания. По финальным вероятностям можно вычислить характеристики эффективности СМО. Сначала найдем Potk - вероятность того, что пришедшая заявка получит отказ. Для этого нужно, чтобы все n каналов были заняты, значит,
Отсюда находим относительную пропускную способность - вероятность того, что заявка будет обслужена:
Абсолютную пропускную способность получим, умножая интенсивность потока заявок
Таким образом, мы нашли интенсивность потока обслуженных системой заявок. Так как каждый занятый канал в единицу времени обслуживает в среднем
3.5.2. Одноканальная СМО с неограниченной На практике довольно часто встречаются одноканальные СМО с очередью (врач, обслуживающий пациентов; телефон-автомат с одной будкой; ЭВМ, выполняющая заказы пользователей). Пусть имеется одноканальная СМО с очередью, на которую не наложено никаких ограничений (ни по длине очереди, ни по времени ожидания). На эту СМО поступает поток заявок с интенсивностью Lсист - среднее число заявок в системе; Wсист - среднее время пребывания заявки в системе; Lоч - среднее число заявок в очереди; Wоч - среднее время пребывания заявки в очереди; Рзан - вероятность того, что канал занят (степень загрузки канала). Что касается абсолютной пропускной способности А и относительной Q, то вычислять их нет надобности: в силу того, что очередь не ограничена, каждая заявка рано или поздно будет обслужена, поэтому А = Решение. Состояния системы будем нумеровать по числу заявок, находящихся в СМО: S0- канал свободен; S1- канал занят, очереди нет; S2- канал занят, одна заявка стоит в очереди; и т.д. Теоретически число состояний ничем не ограничено. Граф состояний имеет вид (рисунок 3.8).
Рисунок 3.8 – Граф состояний одноканальной СМО с неограниченной очередью
Это - схема гибели и размножения, но с бесконечным числом состояний. По всем стрелкам поток заявок с интенсивностью
Ряд в формуле (3.30) представляет собой геометрическую прогрессию. Известно, что при
откуда Вероятности p 1, p 2,..., p k,... найдутся по формулам:
откуда с учетом (3.31) найдем окончательно:
Как видно, вероятности р 0, р 1... образуют геометрическую прогрессию со знаменателем Найдем среднее число заявок в СМО Lсист. Случайная величина Z – число заявок в системе- имеет возможные значения 0,1,2,...,k,... с вероятностями р 0, р 1,..., p k,... Ее математическое ожидание равно
Подставим в (3.33) выражение для р k из (3.32):
Произведение
Но сумма в (3.34) есть не что иное, как сумма бесконечно убывающей геометрической прогрессии с первым членом
Теперь применим формулу Литтла и найдем среднее время пребывания заявки в системе:
Найдем среднее число заявок в очереди Lоч. Будем рассуждать так: число заявок в очереди равно числу заявок в системе минус число заявок, находящихся под обслуживанием. Значит (по правилу сложения математических ожиданий), среднее число заявок в очереди Lоч равно среднему числу заявок в системе Lсист минус среднее число заявок под обслуживанием. Число заявок под обслуживанием может быть либо нулем (канал свободен), либо единицей (канал занят). Математическое ожидание такой случайной величины равно вероятности того, что канал занят (Рзан). Очевидно, Рзан равно 1 минус вероятность р 0 того, что канал свободен:
Следовательно, среднее число заявок под обслуживанием равно
отсюда
и окончательно
По формуле Литтла найдем среднее время пребывания заявки в очереди:
Таким образом, все характеристики эффективности СМО найдены.
3.5.3.Многоканальная СМО с неограниченной Аналогично одноканальной СМО решается задача о многоканальной СМО с неограниченной очередью. Нумерация каналов- опять по числу заявок, находящихся в очереди: S0- все каналы свободны; S1- один канал занят, очереди нет; S2- занято два канала; .................................... Sn- занято n каналов; Sn+1- заняты все n каналов, одна заявка стоит в очереди; ................................... Sn+r- занzты все n каналов, r заявок стоит в очереди; ..................................
Рисунок 3.9 – Граф состояний многоканальной СМО
Граф состояний показан на рисунке 3.9. Граф есть схема гибели и размножения, но с бесконечным числом состояний. Естественное условие существования финальных вероятностей-
Теперь найдем характеристики эффективности СМО. Из них легче всего находится среднее число занятых каналов
Прибавляя к нему среднее число заявок под обслуживанием (оно же- среднее число занятых каналов)
Деля выражение для Lсист и Lоч на
|
||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 159; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.011 с.) |

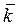
 – среднее число занятых каналов.
– среднее число занятых каналов.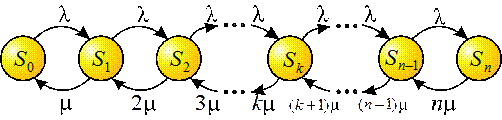
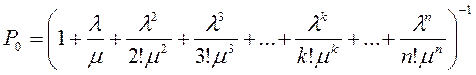 (3.22)
(3.22)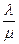 ,...
,... 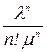 будут представлять собой коэффициенты при P0 в выражениях для P1, P2,...Pn:
будут представлять собой коэффициенты при P0 в выражениях для P1, P2,...Pn: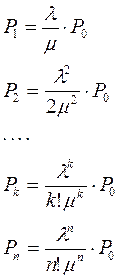 (3.23)
(3.23)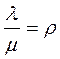 (3.24)
(3.24)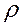 приведенной интенсивностью потока заявок. Ее смысл - среднее число заявок, приходящее за среднее время обслуживания одной заявки. Пользуясь этим обозначением, перепишем формулы (3.22), (3.23) в виде:
приведенной интенсивностью потока заявок. Ее смысл - среднее число заявок, приходящее за среднее время обслуживания одной заявки. Пользуясь этим обозначением, перепишем формулы (3.22), (3.23) в виде: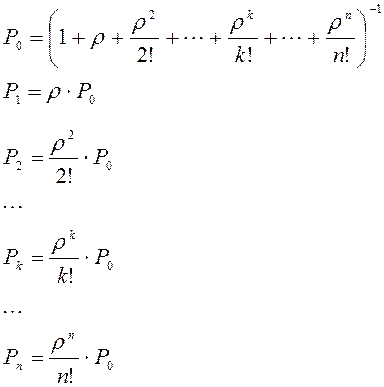 (3.25)
(3.25)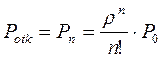 (3.26)
(3.26)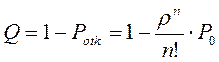 (3.27)
(3.27)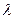 на Q:
на Q: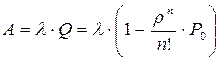 (3.28)
(3.28)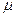 заявок, то среднее число занятых каналов равно
заявок, то среднее число занятых каналов равно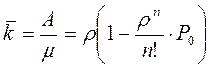 (3.29)
(3.29)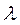 , по той же причине Q=1.
, по той же причине Q=1.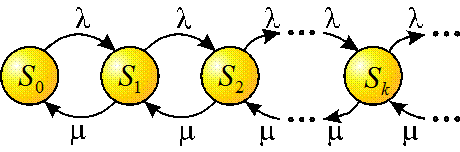
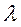 переводит систему слева направо, а справа налево - поток обслуживаний с интенсивностью
переводит систему слева направо, а справа налево - поток обслуживаний с интенсивностью 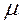 . Если
. Если 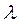 >
> 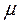 , то канал с заявками не справляется, очередь растет до бесконечности. Если
, то канал с заявками не справляется, очередь растет до бесконечности. Если 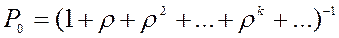 (3.30)
(3.30)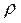 < 1 ряд сходится; при
< 1 ряд сходится; при 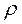 ³ 1 ряд расходится. Теперь предположим, что это условие выполнено, и
³ 1 ряд расходится. Теперь предположим, что это условие выполнено, и 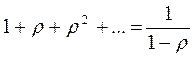
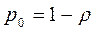 . (3.31)
. (3.31)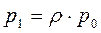 ,
, 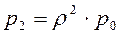 ,...,
,..., 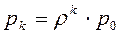 ,...,
,...,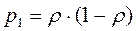 ,
, 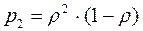 ,...,
,..., 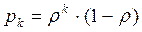 .(3.32)
.(3.32)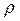 . Как ни странно, максимальная из них р 0- вероятность того, что канал будет вообще свободен. Как бы ни была загружена система с очередью, если только она вообще справляется с потоком заявок, самое вероятное число заявок в системе будет равно нулю.
. Как ни странно, максимальная из них р 0- вероятность того, что канал будет вообще свободен. Как бы ни была загружена система с очередью, если только она вообще справляется с потоком заявок, самое вероятное число заявок в системе будет равно нулю.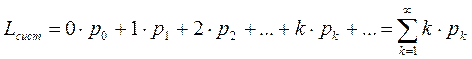 (3.33)
(3.33)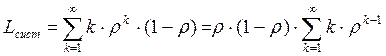
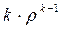 есть ни что иное, как производная по
есть ни что иное, как производная по 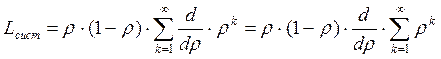 (3.34)
(3.34)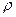 и знаменателем
и знаменателем 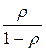 , а ее производная
, а ее производная 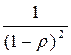 . Подставляя это выражение в (3.34), получим:
. Подставляя это выражение в (3.34), получим: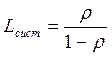 . (3.35)
. (3.35)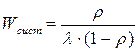 (3.36)
(3.36)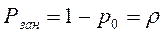 . (3.37)
. (3.37)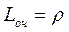 (3.38)
(3.38)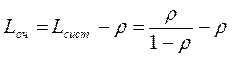
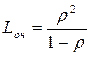 (3.39).
(3.39).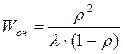 (3.40)
(3.40)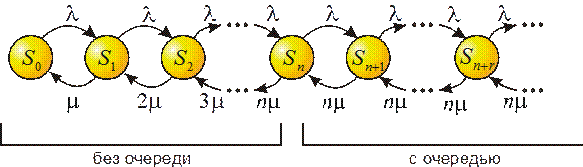
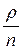 <1. Если
<1. Если 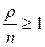 , очередь растет до бесконечности. Предположим, что условие
, очередь растет до бесконечности. Предположим, что условие 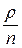 . Суммируя ее, найдем
. Суммируя ее, найдем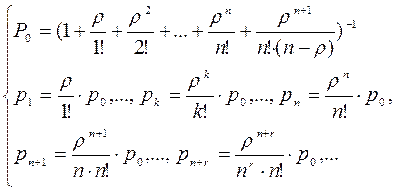 (3.41)
(3.41)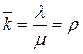 (это вообще справедливо для любой СМО с неограниченной очередью). Найдем среднее число заявок в системе Lсист и среднее число заявок в очереди Lоч. Из них легче вычислить второе по формуле
(это вообще справедливо для любой СМО с неограниченной очередью). Найдем среднее число заявок в системе Lсист и среднее число заявок в очереди Lоч. Из них легче вычислить второе по формуле 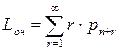 ; выполняя соответствующие преобразования по образцу одноканальной СМО с неограниченной очередью, получим:
; выполняя соответствующие преобразования по образцу одноканальной СМО с неограниченной очередью, получим: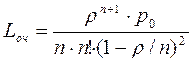 (3.42)
(3.42)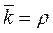 , получаем:
, получаем: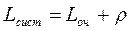 (3.43)
(3.43)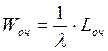 ,
, 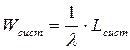 (3.44)
(3.44)


