
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Управление ресурсами вычислительных системСодержание книги
Поиск на нашем сайте
Управление ресурсами однопроцессорных систем оперативной обработки данных Алгоритм SPT В системах оперативной обработки в качестве основного критерия эффективности используется средне время обслуживания заявок. Нетрудно видеть, что в случае, когда времена решения задач априори известны, минимальное среднее время ответа дает алгоритм SPT (Shortest-processing-task-first), назначающий задачи на решение в порядке убывания времени решения ti, то есть t1£t2£...£tL . При этом время ответа ui для задачи zi есть ui= S tj, где S tj- времяожидания, ti- собственно время решения и среднее время ответа есть Покажем, что u* действительно минимальное значение среднего времени обслуживания. Для того чтобы показать, что u* действительно минимально среди u для всех перестановок, достаточно показать, что применение к произвольной перестановке (a1,...,aL) любой парной транспозиции, меняющей местами элементы ak и al, где tal£ tak и l>k, может лишь уменьшить исходное значение u, соответствующее перестановке (a1,...,aL), где ai - номер задачи, назначаемой на решение i-й по порядку, i=I,L. Действительно, пусть задачи с номерами ak и al поменялись местами. Тогда для полученной перестановки среднее время обслуживания равно
Нетрудно видеть, что
так как l > k, а tal £ tak. Следовательно, перемещение вперед задачи с меньшим временем решения приводит к уменьшению среднего времени обслуживания. В перестановке (1,...,L) при условии, что t1 £...£ 7tL, нельзя сделать ни одной такой улучшающей транспозиции, а потому u* есть минимальное среднее время обслуживания и алгоритм SPT дает оптимальное решение рассматриваемой задачи. Алгоритм RR В реальных системах оперативной обработки априорная информация о временах решения задач, как правило, отсутствует. Чтобы воспользоваться принципами планирования на основе алгоритма SPT, в систему вводятся средства, обеспечивающие выявление коротких и длинных работ непосредственно в ходе вычислительного процесса. Простейшее правило планирования работ, обеспечивающее выполнение указанного требования, задается алгоритмом циклического обслуживания, или, иначе, алгоритмом RR (Round–Robin). Работа алгоритма иллюстрируется рисунком 3.10.
Рисунок 3.10 - Циклическое обслуживание заданий
Заявки на выполнение работ поступают с интенсивностью l в очередь O, откуда они выбираются и исполняются процессором Пр. Для обслуживания отдельной заявки отводится постоянный квант времени q, достаточный для выполнения нескольких тысяч операций. Если работа была выполнена за время q, она покидает систему. В противном случае она вновь поступает в конец очереди и ожидает предоставления ей очередного кванта процессорного времени. Оценим среднее время ожидания и пребывания работ в системе с циклическим планированием. Воспользуемся для этого аппаратом теории массового обслуживания. Для упрощения последующих выкладок предположим, что длительность кванта - не постоянная величина, а случайная, распределенная по экспоненциальному закону с тем же средним значением q. Примем также, что на вход системы поступает простейший поток с интенсивностью l работ в единицу времени, и с вероятностями s или (1- s) работа не будет или соответственно будет завершена в текущем кванте. Из последнего предположения следует, что вероятность того, что работа будет выполнена точно за k квантов (не завершена за первые k-1 квантов и завершена в k -том варианте), описывается геометрическим распределением pk= s k-1 (1- s), k=1,2,... со средним
Таким образом, если известны средняя трудоемкость работ Q и длительность q кванта, то среднее количество
Определим среднее время ответа для работы J, требующей ровно t единиц времени обработки. Пусть m – наименьшее целое, при котором mq ³ t (то есть m – число квантов, достаточное для обслуживания заявки). Рассмотрим состояние системы на момент поступления работы J. При поступлении работы J в системе в среднем находится W1 других работ. Значение N1 определяется как среднее число заявок в системе с бесприоритетным обслуживанием, на вход которой заявки поступают с интенсивностью L = l + l s + l s 2 + ¼ + l s n + ¼ = l / (1 - s) (с учетом интенсивности поступления заявок на дообслуживание в последующих тактах) и обслуживаются по экспоненциальному закону со средним q. Для определения W1 требуется найти распределение вероятностей {pk} того, что в очереди будет ровно k заявок. Тогда W1= S kpk. Для определения pk составим систему дифференциальных уравнений Колмогорова с помощью графа переходов (рисунок 3.11). (m = 1 / q)
Рисунок 3.11 – Граф состояний (переходов)
Здесь Si – состояние системы с i заявками в очереди (одна из них обслуживается). Тогда система уравнений имеет вид p`i =Lpi-1 - mpi - Lpi + mpi+1, или æ í p`i =Lpi-1 - (m+L)pi + mpi+1, i=1,2,... è p`0 = -Lp0 + mp1. Кроме того, требуется соблюдение условия нормировки
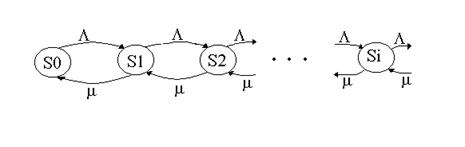
Рассмотрим установившийся режим, то есть считаем, что t®¥. Тогда вместо дифференциальных уравнений получаем алгебраические Lpi-1 - (m+L)pi + mpi+1=0, i=1,2,... Lp0 + mp1=0, p0 + p1 +... + pi +... =1. Из второго уравнения выразим p1 через p0: p1 = L/m* p0 ; подставим это значение в первое уравнение с i=1. Тогда
Делаем индуктивное предположение:
откуда
где
На основании полученного выражения
С учетом допущения об экспоненциальности распределения кванта q время дообслуживания работы J не зависит от этого момента и в среднем равно q. Таким образом, работа будет ожидать W1q единиц времени до получения первого кванта. За время W1q и первый квант выполнения работы J в систему поступит l новых работ. Кроме того, s W1 работ из их общего числа W1 вернутся обратно в очередь на довыполнение. Поэтому в следующем цикле работа J застанет в системе W2 работ: W 2 = l W 1 q + l q + s W 1. Подставляя в последнее выражение ранее полученное значение W1, получаем
В общем случае аналогично получаем Wi = l Wi -1 q + l q + s Wi -1 = r /(1- r). Среднее время ожидания для работы J, время выполнения которой составляет m квантов, равно w m = q Здесь среднее время ожидания w m определяется как время, необходимое для обслуживания всех Wi работ, стоящих впереди работы J в каждом из m циклов обслуживания. Среднее время ответа для работы J Um = w m + mq = mq /(1- r), где r = l q/(1- s) = l q/(q/ Q) = l Q – загрузка системы. Из выражения для времени ожидания wm видно, что время ожидания обслуживания возрастает с увеличением трудоемкости t=mq задачи. В то же время при обслуживании задач в порядке поступления без прерываний среднее время ожидания w не зависит от трудоемкости и составляет где Сравним w и wm:
Из последнего выражения видно, что время ожидания длинных задач (mq> Q) больше, чем при обслуживании в порядке поступления, а время ожидания коротких задач (mq< Q) – меньше времени ожидания в режиме без прерываний.
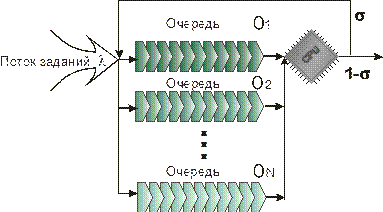
Алгоритм FB Для обеспечения еще более быстрой реакции системы на короткие работы в системах оперативной обработки используются алгоритмы многоуровневого циклического планирования. Одним из таких алгоритмов является алгоритм FB (foreground-background). Принцип его работы можно проиллюстрировать следующей схемой (3.12):
Рисунок 3.12 - Многоуровневая циклическая обработка заданий
Заявки на выполнение работ поступают в очередь O 1. Работы, стоящие в очереди O 1, получают квант процессорного времени q. Если за это время работа была выполнена, то она покидает систему. В противном случае заявка на работу переносится в очередь O 2, откуда она может быть занесена в очереди O 3, O 4,..., O n. Очереди обслуживаются в следующем порядке. Если имеется хотя бы одна заявка в очереди O 1, то эта заявка непременно обслуживается. Заявки из очереди O 2 обслуживаются при условии, что нет заявок в очереди O 1. Аналогично заявки из очереди O m обслуживаются только в том случае, если все очереди O 1,..., O m-1 пусты. Заявка, достигшая последней очереди O n, остается в ней до полного завершения работы. Применяются модификации алгоритма FB, различающиеся по величине квантов времени, предоставляемых заявкам из разных очередей. Возможно планирование на основе постоянной величины кванта или с использованием квантов переменной длительности, которая возрастает по мере увеличения номера очереди. Одна из таких модификаций – алгоритм планирования FB с учетом приоритетов работ. Работы, поступающие в систему, разделяются в зависимости от приоритетов I,..., n на n потоков l1,..., ln. Приоритеты задач относительны, то есть поступление в систему заявки более высокого приоритета не прерывает процесс обработки менее приоритетных заявок, но при освобождении ресурса более приоритетные заявки будут назначены в первую очередь. Работы с высшим приоритетом поступают в очередь O 1, а работы с низким приоритетом – в очередь O n. Работам, выбираемым на обслуживание из разных очередей, выделяются кванты времени различной длительности, причем заявкам из очереди O m выделяется больший по продолжительности квант времени, чем заявкам из очереди O m-1, m = 2, n. Приоритеты работам могут назначаться исходя из трудоемкости последних. Если трудоемкости работ известны хотя бы приближенно, то работам с большой трудоемкостью присваиваются низкие приоритеты и они сразу же поступают в очереди соответствующего приоритета, в которых получают большие кванты времени. В результате этого трудоемкие работы не будут задерживать процесс выполнения менее трудоемких работ. Если трудоемкость работы была занижена, то есть ее приоритет оказался завышен, то после окончания выделенного для нее кванта времени работа переместится в очередь следующего, более низкого приоритета. Алгоритм планирования с учетом приоритетов очень эффективен для систем с ограниченной емкостью оперативной памяти, не позволяющей разместить в ней программы всех работ, выполняемых системой. В таком случае в оперативной памяти размещается только небольшая часть программ, а остальные программы хранятся во внешней памяти – на магнитном диске. Все программы циклически обслуживаются предоставлением им кванта процессорного времени, поэтому они вызываются в оперативную память поочередно, а получив квант обслуживания, удаляются из нее во внешнюю память. Процесс циклического завершения программ в оперативной памяти называется свопингом. Если система работает со свопингом и все без исключения работы поступают в первую очередь, причем всем очередям выделяются одинаковые кванты времени, то затраты ресурсов системы на свопинг крайне большие. Для уменьшения непроизводительных затрат целесообразно трудоемкие работы сразу же размещать в очередях с низкими приоритетами и выделять им большие по длительности кванты времени. Например, операционная система для малых ЭВМ ОСРВ обеспечивает две процедуры разделения времени – циклическое планирование и вытеснение на диск. Процедура циклического планирования через заданный интервал времени циклически перемещает указатель задач в таблице задач системы STD (System Task Directory) и объявляет значимое событие, в результате обработки которого происходит перепланирование задач. Планировщик выбирает для выполнения первую задачу из STD. Обычно интервал времени циклического планирования устанавливается равным 0,1с. Процедура вытеснения на диск перемещает временно на диск часть задач из основной памяти, освобождая тем самым место для более приоритетных задач. Необходимые условия для вытеснения задачи: – задача должна быть установлена как вытесняемая; – на диске есть более приоритетная задача, для которой нет места в основной памяти; – задача не имеет незавершенных запросов ввода-вывода (кроме запроса ввода с терминала). При выполнении процедур вытеснения на диск записываются область занимаемой задачей основной памяти и информация о текущем состоянии задачи, необходимая для продолжения ее работы. Разделение ресурсов задачами базируется на периодическом уменьшении приоритетов задач, находящихся в основной памяти, и как только приоритет задачи в основной памяти становится меньше приоритета задачи на диске, выполняется процедура вытеснения. Приоритетность программ для систем со свопингом может назначаться в соответствии с алгоритмом Корбато. Здесь априорно принимается следующее предположение: программы с большей длиной – более трудоемкие. Исходя из этого предположения приоритеты программам присваиваются на основе формулы
где [x] – целая часть X; Ln – длина программы в байтах; Lq – число байтов, передаваемых между оперативной и внешней памятью за время q, равное минимальной длительности кванта. Отношение qp =2 p -1 q, где q – квант времени, выделяемый для работ из очереди O 1 . Таким образом, очередям O1, O2, O3, O4,... соответствуют кванты времени q,2q,4q,8q,... Увеличение кванта времени на выполнение работ с большой трудоемкостью способствует сокращению числа прерываний работы процессора и числа пересылок программ между оперативной и внешней памятью. Планирование вычислительного процесса
|
||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 336; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |

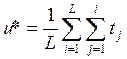 .
.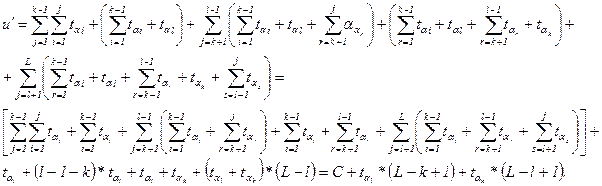
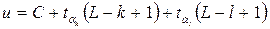 , а потому
, а потому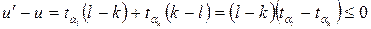 ,
,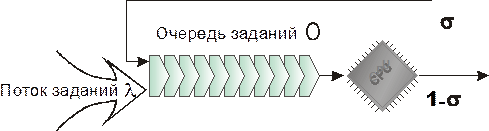
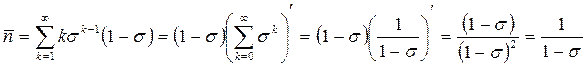
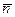 квантов, с одной стороны, равно Q / q, а с другой – полученному выше выражению, то есть
квантов, с одной стороны, равно Q / q, а с другой – полученному выше выражению, то есть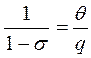 , откуда
, откуда 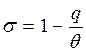 .
.
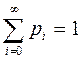 .
. 
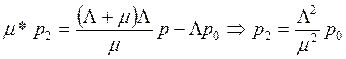
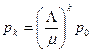 . Тогда из k-го уравнения получаем
. Тогда из k-го уравнения получаем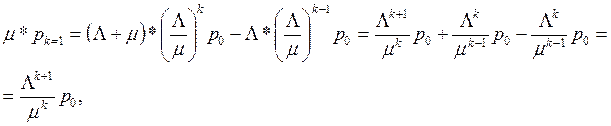
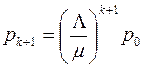 , что подтверждает индуктивное предположение. Поэтому в соответствии с условием нормировки получим
, что подтверждает индуктивное предположение. Поэтому в соответствии с условием нормировки получим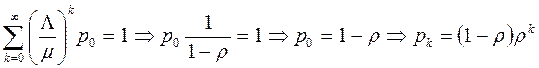 ,
,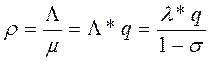 .
.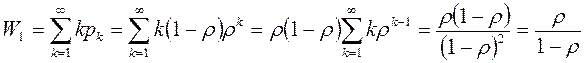 .
.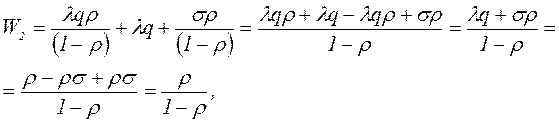
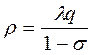
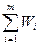 = mq r /(1- r).
= mq r /(1- r).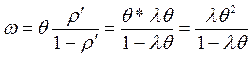 ,
,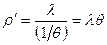 ,
, 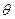 – средняя трудоемкость.
– средняя трудоемкость.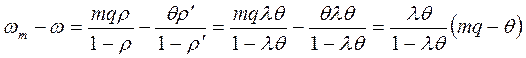 .
.
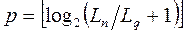 ,
,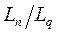 определяет число квантов времени, необходимых для загрузки программы в оперативную память и для вывода ее из оперативной памяти. Работа с приоритетом r заносится в очередь O p. Очередям с номерами
определяет число квантов времени, необходимых для загрузки программы в оперативную память и для вывода ее из оперативной памяти. Работа с приоритетом r заносится в очередь O p. Очередям с номерами 


