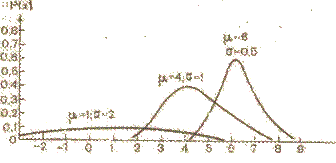Е) творческие результаты в разных видах искусства, материалы средств массовой информации (газеты, журналы и т. п.).

Для того чтобы при изучении документов можно было преодолеть субъективизм исследователя, выявить достоверную информацию и до­статочно точно ее зарегистрировать, был разработан специальный ме­тод, получивший название контент-анализа (буквально «анализ содер­жания»). Впервые он начал применяться начиная с 20-х гг. прошлого столетия для обработки материалов средств массовой коммуникации. Это более или менее формализованный метод анализа документов, когда на основе гипотезы исследователя в документальных материа­лах выделяются специальные единицы информации, а затем подсчи­тывается частота их употребления. Так, например, в 20-е гг. русский исследователь Н. А. Рыбников в ходе анализа сочинений прослежи­вал, как распределяются положительные и отрицательные оценки школьниками своей жизни в зависимости от возраста и пола. Или дру­гой пример: в 80-х гг. Н. Н. Лепехиным и Ч. А. Шакеевой проводился контент-анализ эпизодов жестокости и агрессии в западных и отече­ственных кинофильмах.

Таким образом, основная процедура контент-анализа связана с перево­дом качественной информации на язык счета. С этой целью выделяются два типа единиц: смысловые, или качественные, единицы анализа и еди­ницы счета, или количественные. Основная трудность при работе с доку­ментальными источниками — умение провести качественный анализ, т. е. выделить смысловые единицы. Это во многом зависит от личной компетентности исследователя, уровня его творческих возможностей.

Так как контент-анализ основан на принципе повторяемости, частоты использования различных смысловых единиц (например, определен­ных понятий, суждений, образов и т. п.), его следует применять только тогда, когда есть достаточное количество материала для анализа.

В контент-анализе от простого подсчета частот встречаемости тех или иных смысловых единиц постепенно перешли к более сложным статистическим приемам (корреляционной технике и факторному анализу). Новым этапом в развитии этого метода стала его компьюте­ризация. Особенно широко это используется в США — там разрабаты­ваются стандартные программы анализа разнообразных документов, позволяющие достаточно быстро и надежно проанализировать огром­ный объем информации и освободить кодировщиков от утомительно­го ручного способа.

В психологической диагностике контент-анализ наиболее часто исполь­зуется в качестве вспомогательного метода или процедуры обработки данных, полученных при других исследованиях. С его помощью подвер­гаются анализу речевые сообщения испытуемого, сопровождающие практически любые диагностические обследования, особенно при инди­видуальной процедуре. Конкретно контент-анализ может применяться при обработке данных, полученных посредством проективных методик (например, ТАТ, методика Роршаха, Завершение предложения), интер­вью, содержания бесед, другой речевой и письменной продукции испы­туемого, открытых вопросов анкет и т. п. Так, например, в методиках диа­гностики личностных особенностей (тревожности, невротизма и др.) проводится контент-анализ грамматических и стилистических конструк­ций речи испытуемого: количество «тематических» высказываний (бо­лезнь, страх, неуверенность и т. д.), глаголов, логических блоков и т. п. Такой анализ нередко позволяет выявить и объективизировать скрытую тенденцию в ответах испытуемого.

Следует коротко остановиться еще на одном классе методик. В по­следнее время в западной психологической литературе появился термин «тесты учителя». Под ним подразумеваются не только традиционные тесты учета и контроля школьных достижений, а целенаправленное использование учителем в своей работе малоформализованной диа­гностики. В частности, выделяется умение проводить систематические наблюдения, имеющие своей целью изучение индивидуально-психо­логических особенностей учеников, их поведения. По основательнос­ти разработки тесты учителя далеко отстают от того, что достигнуто в формализованной диагностике. Однако само их появление в психо­диагностической литературе следует рассматривать как одно из про­явлений неудовлетворенности той формалистичностью, которая стала неотъемлемой особенностью психологического диагностирования. Только сочетание формализованных методов диагностики с наблюде­ниями, беседами, тестами учителя и подобными формами изучения обследуемого может дать удовлетворяющий результат.

 

Психометрические требования к построению и проверке методик

Психометрия — область психологической диагностики, связанная с теорией и практикой измерений в психологии.

Это понятие было введено немецким исследователем X. Вольфом, который ставил перед собой задачу измерить величину внимания по­средством продолжительности аргументации, за которой человек в со­стоянии проследить.

Реализация идеи измерений психических явлений началась с работ по психофизике. Первоначально под психометрией понималось из­мерение временных характеристик психических процессов. Однако очень скоро область психометрии расширялась — к ней стали относить измерения не только ощущений, но и более сложных психических функций. Другими словами, все то, что связано с количественным оп­ределением психических явлений, стали включать в понятие «психо­метрия», которое затем переросло в понятие «общая психометрия».

С появлением такой области исследований, как дифференциальная психология, психометрия получила свое новое развитие, поскольку ста­ли возникать особые правила и требования к принципам измерения, следование которым обеспечивало его точность и достоверность. В связи с этим обнаружилась необходимость использовать понятие, более точно определяющее данную область измерений. Оно должно было отражать не всю совокупность психологических и психофизических измерений, а только ту, которая имеет отношение к дифференциально-психологи­ческим характеристикам. В качестве такого понятия предлагается ис­пользовать термин «дифференциальная психометрия».

В ряде работ по психологической диагностике обосновывается це­лесообразность отличать понятие «дифференциальная психометрия» от понятия «общая психометрия». Как первое, так и второе понятие связано с теорией и практикой измерений в психологии. В то же время важно отметить следующее.

К общей психометрии относятся измерения общепсихологического (свойственного всем людям) характера, т. е. функциональные за­висимости между свойствами стимула и свойствами субъектив­ных реакций. Так, в психофизике определяется зависимость меж­ду физическими характеристиками стимулов и субъективными характеристиками ощущений (например, объективная прибавка веса и порог субъективного ощущения увеличения тяжести). В социально-психологических областях выявляется соответствие между рядами социальных объектов и психологическими реак­циями (например, социальные объекты — разные виды реклами­руемых товаров, психологические реакции — от «очень нравится» до «очень не нравится»).

 К дифференциальной психометрии относятся измерения, каса­ющиеся индивидуальных различий между людьми по способнос­тям, когнитивным функциям (внимание, память, мышление и т. д.), мотивам, эмоциональным особенностям и пр. Здесь числовые зна­чения (баллы, ранги, шкальные значения) приписываются не сти­мулам, а индивидам.

Дифференциальная психометрика по отношению к психодиагнос­тике и дифференциальной психологии выступает в качестве техноло­га-методической дисциплины. Она обосновывает требования, которым должны удовлетворять психодиагностические методики, процедуру их разработки и применения. К числу таких требований относятся стандартизация, надежность и валидность методик.

Выше говорилось о том, что психодиагностические методики назы­вают измерительными инструментами. Однако возникает вопрос, пра­вомерно ли их так называть, являются ли они таковыми, подобными, например, тем, которые используются в физических измерениях?

Ответ на этот вопрос можно найти в работах К. М. Гуревича. На примере анализа тестов он показывает, что такое определение диагностических методик носит условный характер. Сначала нужно вспомнить, что представляет собой измерение. Измерить — значит определить какой-либо мерой величину измеряемого. Для этого нуж­но, чтобы были соблюдены по крайней мере два условия.

Первое условие касается самого измерительного инструмен­та: он должен иметь на протяжении всего измерения одну и ту же, тож­дественную самой себе меру. Нельзя измерять инструментом, у которого нет такой тождественной самой себе меры (например, если бы на линей­ке расстояния от одного деления до другого были неодинаковы на раз­ных участках). Второе условие — нужно, чтобы то, что измеряется, во всех случаях оставалось одним и тем же, т. е. также было тождественно самому себе. К. М. Гуревич считает, что соблюсти эти два условия в психодиагностических исследованиях крайне затруднительно.

Например, в тесте предложены задания на умение производить такую логическую операцию, как классификация понятий. Так, даны понятия пшеница, чечевица, кукуруза, бамбук, ячмень. Испытуемый должен за­черкнуть слово, которое не подходит к четырем основным. Обычно ис­пытуемые зачеркивают бамбук. Это ошибка. Бамбук, как пшеница, яч­мень и кукуруза, относится к злаковым, а чечевица— к бобовым. Это слово и следует зачеркнуть.

Чем можно объяснить, что не все испытуемые дают правильный ответ?

К. М. Гуревич называет несколько причин:

1) испытуемый слабо владеет такой логической операцией, как клас­сификация;

2) испытуемый владеет логической операцией, но не знает того ма­териала, на котором ее надо применить;

3) испытуемый знает материал, владеет логической операцией, но он не способен работать в том обычно довольно быстром темпе, ко­торый требуется при выполнении теста.

Возникает вопрос, что же измеряет в действительности данное задание?

Как было показано выше, у одних испытуемых оно измеряет что-то одно, у других — другое. У испытуемых, владеющих соответствующим материалом, оно измеряет то, на что направлено, — владение логиче­ской операцией. У тех же испытуемых, которым материал задания мало­знаком, измеряется их знание. Кроме того, у тех и других измеряется их индивидуальный темп.

Этот анализ К. М. Гуревич продолжает дальше. Тест состоит из цело­го набора заданий; иногда их число доходит до 40. Можно ли выполнен­ное задание считать мерой, через которую определяется количествен­ный показатель измеряемой стороны психики?

Нельзя, так как эта мера измеряет разные стороны психики. У одних вы­является владение логическими действиями, у других — знание тех по­нятий, которые представлены в тесте, у третьих фактически измеряется их темп; у одних эта мера имеет одно, а у других — другое содержание.

На основании проведенного анализа К. М. Гуревич делает вывод о том, что данные, которые получаются в тестировании, нельзя считать из­мерениями в подлинном смысле слова. Тест не является измерительным инструментом в том понимании, которое существует, например, в фи­зических измерениях, хотя какую-то оценку той стороны психики, на диагностирование которой он направлен, тест показывает — правда, не в количественном выражении.

Тест можно считать инструментом сравнения. При сравнении не подчеркивается, что из двух сравниваемых объектов один больше дру-

гого на столько-то единиц. В этом случае достаточно установить, что такой-то объект больше другого (или других). По результатам сравне­ния можно расположить все изучаемые объекты в определенном по­рядке — от меньшего к большему или наоборот. Сравнение не предпо­лагает обязательного измерения, а значит, не предполагает и единицы измерения. При сравнении устанавливается только последовательность, порядок сравниваемых объектов по их величине.

Сделанный К. М. Гуревичем вывод относительно тестов с полным правом может быть перенесен и на другие диагностические методики.

 

Стандартизация

Диагностическая методика отличается от любой исследовательской тем, что она стандартизирована. Как отмечает А. Анастази, стандарти­зация — это единообразие процедуры проведения и оценки выпол­нения теста.

Стандартизация рассматривается в двух планах:

- выработка единых требований к процедуре экспе­римента;

- определение единого критерия оценки результатов диа­гностических испытаний.

Стандартизация процедуры эксперимента подразумевает унифи­кацию (единообразие) инструкций, бланков обследования, способов регистрации ре­зультатов, условий проведения обследования.

К числу требований, которые необходимо соблюдать при проведе­нии эксперимента, можно отнести такие:

· инструкции следует сообщать испытуемым одинаковым образом, как правило, письменно; в случае устных указаний они даются в разных группах одними и теми же словами, понятными для всех, в одинаковой манере;

· ни одному испытуемому не следует давать никаких преимуществ перед другими;

· в процессе эксперимента не следует давать отдельным испыту­емым дополнительные пояснения;

· эксперимент с разными группами следует проводить в одинако­вое по возможности время дня, в сходных условиях;

· временные ограничения в выполнении заданий для всех испыту­емых должны быть одинаковыми и т. д.

Обычно авторы методики в руководстве приводят точные и подроб­ные указания по процедуре ее проведения. Формулирование таких указаний составляет основную часть стандартизации новой методики, так как только строгое их соблюдение дает возможность сравнить между собой показатели, полученные разными испытуемыми.

Другим важным моментом в стандартизации методики является выбор критерия, по которому следует проводить сравнение результа­тов диагностических испытаний, поскольку диагностические методи­ки не имеют заранее определенных стандартов успешности или неуда­чи в их выполнении.

Так, например, ребенок шести лет, выполняя тест умственного развития, получил балл, равный 117.

Хорошо это или плохо?

Часто ли такой показатель встречается у детей данного возраста?

Количественный результат как таковой ничего не означает. Получен­ный дошкольником балл нельзя интерпретировать как показатель отно­сительно высокого, среднего или низкого развития, так как это развитие выражено в мерах, присущих данной методике, и, таким образом, аб­солютного значения полученные результаты иметь не могут. Очевидно, нужно располагать точкой отсчета и какими-то дозированными мерами, чтобы с их помощью оценивать полученные при диагностировании ин­дивидуальные и групповые данные.

Возникает вопрос, что за эту точку отсчета брать?

· В традиционном тестировании такая точка добывается статистиче­ским путем — это так называемая статистическая норма – показывает степень отклонения индивидуального показателя от среднегруппового. 

· В некоторых случаях экспериментатору необходимо оценить место, которое занимает испытуемый в популяции по исследуемому показателю. Это возможно при использовании квантильной стандартизации.

· Иной подход к оценке результатов диагностических испытаний предполагает в качестве точки отсчета использовать не зависимый от резуль­татов испытания, объективно заданный тестом социально-психологический норматив. СПН отражает степень близости индивидуальных результатов к нормативу. 

В общих чертах стандартизация ПД методики, ориен­тированной на статистическую норму, осуществляется путем ее проведения на боль­шой репрезентативной выборке того типа, для которой данная мето­дика предназначена. Относительно этой группы испыту­емых, называемой выборкой стандартизации, разрабатываются нормы, указывающие не только средний уровень выполнения, но и его отно­сительную вариативность выше и ниже среднего уровня. В результате можно оценить разные степени успешности или неуспешности в вы­полнении диагностической пробы. Это позволяет определить положе­ние конкретного испытуемого относительно нормативной выборки или выборки стандартизации.

Стандартизация относительно статистической нормы основана на так называемой аксиоме нормальности, т. е. опирается на предположение, что все психические характеристики распределены в популя-
ции по нормальному закону Гаусса. Нормальное распределение полностью
определяется значениями двух параметров: генеральной средней (х) стандартного отклонения (сигма). Положение кривой распределения в системе координат задается значением х, а степень ее крутизны или растянутости — величиной сигма. На рисунке 1. представлено графическое изображение функций Р(х) с различными значениями х, и сигмы. По оси абсцисс отложены значения тестовых оценок, а по оси ординат — плотность вероятности этих значений.

Рисунок 1.

 

Из рисунка 1. видно, что интерпретация тестовых оценок невозможна без знания того, к какой кривой распределения они принадлежат, т. е. для того, чтобы оценить величину тестовой оценки и частоту ее реализации, необходимо соотнести их с генеральной средней х, и стандартным отклонением сигма. Без этого исходные тестовые оценки ничего не скажут нам о степени выраженности исследуемой характеристики и о вероятности появления такого ее значения у других лиц. Вместе с тем именно эта информация особенно интересует экспериментатора, поскольку чаще всего тестовые обследования проводятся для сравнения испытуемых по исследуемой психологической характеристике.

По исходным оценкам мы можем судить только о
том, что чем выше оценка, тем больше выражена соответствующая характеристика, но о том, какова она по отношению к среднему значению этого свойства в популяции, мы ничего сказать не можем.

При нормальном распределении все изучаемые величи­ны практически находятся в пределах [х ± 5сигма]. Нормальное распределе­ние обладает многими преимуществами, в частности, оно позволяет заранее рассчитать, сколько случаев будет расположено в определен­ном удалении от среднего арифметического при использовании для определения удаленности стандартного отклонения. Для этого име­ются специальные таблицы. Из них видно, что в пределах [х ± сигма] нахо­дится 68 % изучаемых случаев. За этими пределами — 32 % случаев, а так как распределение симметрично, то по 16 % с каждой стороны. Итак, преобладающая и наиболее представительная часть распределе­ния находится в пределах [х ± сигма]. Все расчеты и рассуждения нужны только для того, чтобы дать оценку индивидуальным данным, получа­емым при выполнении тестов.

Предположение о нормальности распределения тестовых результатов является некоторой идеализацией. Результаты диагностических испытаний в психологии очень редко укладываются в рамки нормального закона; их приходится для этого специально подгонять. Причины этого явления нужно искать в самом существе теста, в обусловленности его выполне­ния подготовкой испытуемых. Поэтому часто возникает вспомогательная задача нахождения способа преобразования данных к нормальному виду. В самом начале поиска способа преобразования большую помощь может оказать построение гистограммы и полигона распределения. Они позволяют легко выявить лево- или правостороннюю асимметрию, двугорбость и другие отклонения от нормальности. В психологических исследованиях часто встречаются логарифмические нормальные распределения, особенностью которых является крутая левая ветвь полигона и пологая правая (т. е.
частоты резко падают с ростом тестовых оценок). При логарифмировании исходных тестовых данных левая ветвь кривой распределения растягивается и распределение принимает приближенно нормальный вид.

Для нормализации распределений с правосторонней асимметрией используются тригометрические и степенные преобразования данных. Таким образом удается преобразовать тестовые оценки, не подчиняющиеся за-
кону нормального распределения, чтобы распределение новых, преобразованных оценок стало нормальным.

Кроме статистической нормы, основой для сравнения, интерпрета­ции результатов диагностических испытаний может стать квантильная стандартизация.

В некоторых случаях знания степени отклонения индивидуального результата от среднегруппового бывают недостаточны. Экспери-
ментатору необходимо оценить место, которое занимает
испытуемый в популяции по исследуемому показателю, т. е. узнать, какой процент испытуемых выполняет тест хуже или лучше обследованного лица, имеет более высокие или более низкие оценки и т. п. Для этого используют интервальные оценки места испытуемого в популяций. С
этой целью ось накопленной частоты разбивается на фиксированное число равных интервалов. Точка на оси накопленной частоты, делящая ось в установленной пропорции, называется квантилем, поэтому этот вид
стандартизации называется квантильной стандартизацией (3, 18).

Квантиль — это общее понятие, а квартили, квинтили, децили и процентили — его наиболее частные реализации. Имеются, например, три квартиля (Q1, Q2, Q3), которые делят выборку на четыре равные части (кварты) таким образом, что 25% испытуемых располагаются
ниже Qi, 50% — ниже Q2 и 75% — ниже Q3. Четыре квинтеля (К1, К2, К3, K4) делят выборку аналогичным образом на пять, девять децилей (D1, …, D9) — на десять, а 99 процентилей (Р1, …, Р99) — на 100 равных частей. Взаимоотношение между различными квантилями показано на рисунке 4.

Номер квантиля используется в качестве новой преобразованной тестовой оценки. Он показывает относительное положение испытуемого в нормативной выборке. Например, квартальная оценка 3 и процентильная оценка 75 указывают, что более высокую тестовую оценку могут иметь только 25% испытуемых.

Процентили не следует смешивать с обычными процентными пока­зателями. Последние являются первичными показателями и представ­ляют собой процент правильно выполненных заданий, тогда как процентиль — это производный показатель, указывающий на долю от об­щего числа членов группы. Их также можно рассматривать как ранговые градации, общее число которых равно 100, с той лишь разницей, что при ранжировании принято начи­нать отсчет сверху, т. е. с лучшего члена группы, получающего ранг 1. В случае же процентилей отсчет ведется снизу, поэтому чем ниже про­центиль, тем хуже позиция индивида.

Первичный результат, который ниже любо­го показателя, полученного в выборке стандартизации, имеет нулевой процентильный ранг (Р0). Результат, превышающий любой показатель в выборке стандартизации, получает процентильный ранг 100 (Р100). Эти процентили, однако, не означают нулевого или абсолютного ре­зультата выполнения теста.

Для определения стандартизованных квантильных
оценок по методике находятся проекции квантилей на ось
тестовых оценок (см. рис. 4). Проекции квантилей образуют на оси тестовых оценок неравноинтервальную шкалу (рис. 5). Если исходные тестовые оценки распределены по нормальному закону, то проекции квантилей в окрестности средней арифметической расположены плотнее и расстояние между ними возрастает по мере удаления от центра распреде-
ления.  

Квантильная стандартизация является методом стандартизации, как бы противоположным методу, предложенному Р. Б. Кэттеллом.  Метод
Р. Б. Кэттелла группирует тестовые оценки, а квантильный метод группирует испытуемых.

Квантильные показатели обладают рядом достоинств, в частности:

1) их легко рассчитать и понять даже сравнительно неподготовлен­ному человеку;

2) их применение достаточно универсально и подходит к любому типу тестов.

Однако недостаток квантильных показателей — это существенное неравенство единиц отсчета в том случае, когда анализируются крайние точки рас­пределения. При использовании квантилей (как уже отмечалось вы­ше) определяется только относительное положение индивидуальной оценки, но не величина различий между отдельными показателями.

В ПД существует и другой подход к оценке результатов диагностических испытаний. В нашей стране под руководством К. М. Гуревича разрабатываются тесты, в которых в качестве точки отсчета выступает не статистическая норма, а не зависимый от резуль­татов испытания, объективно заданный социально-психологический норматив. СПН реализуется в совокупности заданий, составляющих тест. Следовательно, сам тест в полном его объеме и является таким нормативом. Все сопоставле­ния индивидуальных или групповых результатов тестирования про­водятся с тем максимумом, который представляется в тесте (а это пол­ный набор знаний). В качестве критерия оценки выступает показатель, отражающий степень близости результатов к нормативу. Имеется раз­работанная схема представления групповых количественных данных. Для анализа данных относительно их близости к СПН, условно рассматриваемому как 100 %-ное вы­полнение всего теста, все испытуемые подразделяются по результатам тестирования на пять подгрупп:

1) наиболее успешные — 10 %;

2) близкие к успешным — 20 %;

3) средние по успешности — 40 %;

4) мало успешные — 20 %;

5) наименее успешные — 10 %.

Для каждой из подгрупп подсчитывается средний процент правиль­но выполненных заданий. Далее строится система координат, где по оси абсцисс идут номера подгрупп, по оси ординат — процент выпол­ненных каждой из подгрупп заданий. После нанесения соответству­ющих точек вычерчивается график, отражающий приближение каж­дой из подгрупп к СПН. Такая обработка проводится по результатам как теста в целом, так и каждого субтеста в отдельности.

Таким образом, в процессе подготовки тестов к
практическому использованию тестовые результаты
претерпевают несколько преобразований: приведение к
нормальному виду, приведение к стандартной форме (статистическая норма),
квантильная группировка и возможно группировка по степени близости к СПН. Первые  три вида преобразований следует рассматривать не как самостоятельные и независимые процедуры, а как последовательность шагов представления результатов тестирования в виде, удобном для осмысления и интерпретации.

Выборка стандартизации

При разработке и применении любой точки отсчета следует обращать особое внимание на выборку испытуемых, на которой проводится стандартизация диагностической методики. В математической стати­стике принято различать такие понятия, как генеральная совокупность (популяция) и выборка.

Всякая большая совокупность людей, которую хотели бы иссле­довать или относительно которых собираются делать выводы, назы­вается генеральной совокупностью.

Выборка — это часть или подмножество совокупности. Проводить исследование всей популяции не принято. Обычно из нее выделя­ют группу людей — выборку стандартизации, — которая реально под­вергается тестированию, и с ее помощью оценивается генеральная со­вокупность. Чтобы оценки носили достоверный характер, выборка должна быть репрезентативна, представительна рассматриваемой по­пуляции, т. е. ее вероятностные свойства должны совпадать или быть близкими к свойствам генеральной совокупности.

А. Анастази приводит пример формирования репрезентативной вы­борки при стандартизации шкалы Векслера. Выборка включала 1700 человек с равным количеством мужчин и женщин. Испытуемые в возрасте от 16 до 64 лет были распределены по семи возрастным уровням. При формировании выборки исследователи опирались на данные последней переписи населения США. Учитывалось пропорцио­нальное распределение населения по географическим районам, при­надлежность к городскому и сельскому населению, принадлежность к белой или цветной расе, учитывались также уровень образования и профессия. На каждом возрастном уровне в выборку были введены один мужчина и одна женщина, находящиеся в учреждениях для умствен­но отсталых.

По мнению А. Анастази, подавляющее большинство диагности­ческих методик стандартизовано не для столь широких популяций, как многие полагают. Трудно рассчитывать, что по какому-либо те­сту имеются адекватные нормы для таких обширных популяций, как,

например, «взрослые американцы-мужчины» или «американские де­ти 14-летнего возраста». Выборки, ориентированные на широкие по­пуляции, не всегда репрезентативны и чаще всего бывают смещены в тех или иных отношениях (т. е. некоторые подгруппы популяции могут быть представлены непропорционально своей численности). Так, если определить популяцию как «14-летние дети», а выборку стандартизации составить из 14-летних школьников, то ее нельзя рас­сматривать в качестве репрезентативной, поскольку не все 14-летние дети являются школьниками. В этом случае лучше сузить определе­ние популяции (т. е. определить ее как «14-летние школьники»), чем переносить нормы, полученные на школьниках, на популяцию 14-лет­них детей.

Таким образом, одним из способов обеспечения репрезентативности выборки является ограничение популяции. Ограничить популяцию можно по разным признакам: по возрасту, полу, социальному проис­хождению, профессии, социально-экономическому статусу, здоровью и т. д. Такая популяция определяется как специфическая, и стандар­тизация диагностических методик осуществляется на узконаправ­ленных выборках, которые репрезентативны специфической попу­ляции. Создатель диагностической методики должен всегда сообщать, для какой специфической популяции были разработаны нормативные показатели.

Отбор испытуемых в выборку стандартизации осуществляется сле­дующим образом:

1) дается определение популяции с выделением в ее структуре пе­ременных, значимых и малозначимых для изучаемого психиче­ского явления (возраст, образование, профессия и т. д.);

2) популяция делится на части в соответствии со значимыми пере­менными;

3) испытуемые отбираются в случайном порядке и пропорциональ­но численности каждой значимой части совокупности.

Случайный отбор может осуществляться по алфавиту, по таблице случайных чисел или другим способом. Важно, чтобы у всех предста­вителей популяции были равные шансы попасть в выборку стандар­тизации. Это условие подразумевает, что каждый выбор не зависит от остальных.

Объем выборки может варьироваться в широких пределах, но ее минимальный порог, необходимый для получения достоверных ре­зультатов, — порядка 200 человек.

 

Надежность.

Надежность — характеристика ме­тодики, отражающая точность ПД измерений, а также устой­чивость результатов теста к действию посторонних случайных факторов.

Сущность проблемы надежности теста хорошо иллюстрируется следующим примером. У нас есть часы. Сейчас они показывают ровно 9 утра. Мы предполагаем, что через 60 мин «истинного времени» короткая стрелка окажется на цифре 10, а длинная на 12, т.е. на наших часах будет ровно 10 утра. А еще через 60 минут — ровно 11 и т. д.

Когда же наши часы то спешат, то отстают, мы не можем им доверять (ведь в этом случае мы не в состоянии даже приблизительно сказать, сколько прошло времени после какого-то события). Если в тот момент, когда по радио передают сигналы точного времени, наши часы показывают то пять минут следующего часа, то без пяти, а то вообще половину, их можно просто выбросить, поскольку они ненадежны. Навряд ли мы станем ориентироваться на них, когда нам назначена какая-то важная встреча.

Надежность теста как раз и показывает, насколько ровно идут часы. Если сегодня Вася по тесту интеллекта оказывается в числе лучших в классе, а завтра — в числе худших, то тестирование не имеет ничего общего с инструментами психодиагностического исследования.

   В самом широком смысле надежность теста — это характеристика того, в какой степени выявленные у испытуемых различия по тестовым результатам являются отраже­нием действительных различий в измеря­емых свойствах, и в какой мере они могут быть приписаны случайным ошибкам.

Результат психологического исследо­вания обычно подвержен влиянию боль­шого количества неучитываемых факто­ров. Поэтому важной проблемой практической диагностики является выяснение факторов, снижающих точность измерений и их классификация. Ана­лиз позволил выявить, что среди факторов, снижающих точность измерений наиболее часто называют следующие:

· нестабильность диагностируемого свойства;

· несовершенство диагностических методик (небрежно составле­на инструкция, задания по своему характеру разнородны, нечет­ко сформулированы указания, как методику предъявлять испы­туемым, и т. д.);

· меняющаяся ситуация обследования (разное время дня, когда проводятся эксперименты, разная освещенность помещения, на­личие или отсутствие посторонних шумов и т. д.);

· различия в манере поведения экспериментатора (от опыта к опы­ту по-разному предъявляет инструкции, по-разному стимулиру­ет выполнение заданий и т. д.);

· колебания в функциональном состоянии испытуемого (в одном эксперименте отмечается хорошее самочувствие, в другом — утом­ление и т. д.);

· элементы субъективности в способах оценки и интерпретации ре­зультатов (когда ведется протоколирование ответов испытуемых, оцениваются ответы по степени полноты, оригинальности и т. п.).

   Если все эти факторы иметь в виду и постараться в каждом из них устранить условия, снижающие точность измерений, то можно до­биться приемлемого уровня надежности теста. Одним из важнейших средств повышения надежности психодиагностических мето­дик яв­ляется стандар­тизация процедуры исследования, существенно позволяющая уменьшить влияние посторонних случайных факторов на результаты теста и таким образом повысить их надежность.

На характеристику надежности методик большое влияние оказы­вает исследуемая выборка. Она может, как снижать, так и завышать показатель надежности.

Например, надежность может быть искусственно завышена, если в выбор­ке небольшой разброс результатов, т. е. если результаты по своим значе­ниям близки друг к другу. В этом случае при повторном обследовании новые результаты также расположатся тесной группой. Возможные изме­нения ранговых мест испытуемых будут незначительными, и, следователь­но, надежность методики будет высокой. Такое же неоправданное завышение надежности может возникнуть при анализе результатов выборки, состоящей из группы, имеющей очень высокие результаты, и из группы с очень низкими оценками по тесту. Тогда эти далеко отстоящие друг от дру­га результаты не будут перекрываться, даже если и вмешаются в условия эксперимента случайные факторы.

 Поэтому в руководстве обычно делает­ся описание выборки, на которой определялась надежность методики. В настоящее время надежность все чаще определяется на наиболее однородных выборках, т. е. на выборках, схожих по полу, возрасту, уровню образования, проф подготовке и т. п. Для каж­дой такой выборки приводятся свои коэффициенты надежности. Если методика применяет­ся к выборке, отличающейся от той, на которой проверялась ее Н., то эта процедура должна быть проведена заново.

Распределение оценок испытуемых при выполнении теста, измеряющего одно качество, в идеальном случае совпадает с нормальным распределением, и диспер­сия при этом будет «истинной» (т. е. от­ражающей вариативность только измеря­емого признака). В реальности, на результаты измерений влияют случайные посторонние факторы, соответственно величина реальной эмпирической дисперсии чаще несколько больше дисперсии истинной. Отношение квадратов дисперсий «истинной» (Sист) и эмпирической (Sэмп) дисперсий служит основным показателем точности и устойчивости измерений и называется коэффициентом надежности методик (r):

                       r = S ист

                                 Sэмп

Таким образом, значения r могут колебаться от 0 до 1. Надежность тем выше, чем ближе коэффициент надежности подходит к единице, и наоборот. На практике в большинстве применя­емых м