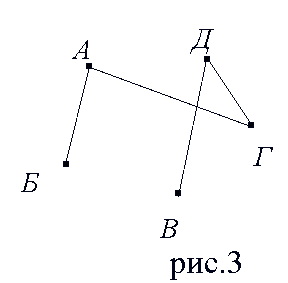Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Практическое занятие №9 . Треугольник Паскаля. Бином Ньютона. Комбинаторные схемы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Элементы теории Составим таблицу значений сочетаний Cnm для n,m = 0,1,2,3,4,5,6,7.
Коэффициенты в правых частях этих формул взяты из строк треугольника Паскаля соответственно с номерами 1,2,3. При любом натуральном n справедлива формула, называемая бином Ньютона:
Коэффициенты в правой части формулы называют разложением степени биномаберутся и з строки с номером n треугольника Паскаля. Если вычисляется (а - b)n = (a + (-b))n, то в правой части формулы знаки чередуются. Задания для самостоятельного выполнения
1. Запишите разложение бинома:
Практическое занятие №10. Графы. Виды графов. Изоморфизм графов.
Элементы теории Любая система, предполагающая наличие дискретных состояний или наличие узлов и переходов между ними может быть описана графом. Соединения между узлами (V) графа называются ребрами (E). Если узлы графа не нумерованы, то ребра являются неориентированными. У графа с нумерованными узлами ребра ориентированы и называются дугами
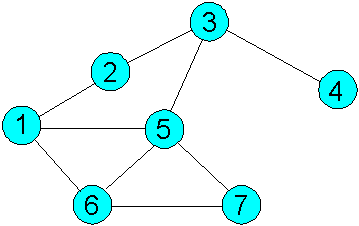
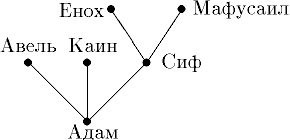
Число ребер, исходящих из вершины vi (петля учитывается дважды), называется валентностью (степенью вершины) и обозначается: d (vi). Если V и E конечные множества, то и граф им соответствующий называется конечным. Граф называется вырожденным, если он не имеет ребер. Неориентированный граф называется простым, если он не имеет петель и любая пара вершин соединена не более чем одним ребром. Графы отображаются на плоскости набором точек и соединяющих их линий или векторов. Грани могут отображаться и кривыми линиями, а их длина не играет никакой роли. Граф G называется планарным (плоским), если его можно отобразить в плоскости без пересечения его граней (рис. 5). Граф называется связным, если для любых двух вершин существует последовательность ребер их соединяющая (рис. 3), т.е. граф не имеет изолированных фрагментов (вершин, ребер). Граф называется полным, если любые две вершины соединены только одним ребром (рис.4). Если полный граф имеет n вершин, то количество ребер будет равно n(n-1)/2. Специальными видами графов являются деревья (рис. 6), кольца и списки, что не входит в рассмотрение нашего курса. Граф, у которого все вершины имеют одну и ту же степень, называется регулярным графом.
Ребро (дуга) и любая из его вершин называются инцидентными. Принято говорить, что ребро (дуга) (u, v) соединяет вершины u и v. Если вершина не инцидентна ни одному ребру (дуге), то она называется изолированной (d(vi)=0), если принадлежит только одному ребру (дуге), то называется висячей (d(vi)=1). Основные положения о вершинах графа: 1. В графе G сумма степеней всех его вершин — число четное, равное удвоенному числу ребер графа, так как каждое ребро участвует в этой сумме ровно два раза. Этот результат называют леммой о рукопожатиях: если несколько человек обменялись рукопожатиями, то общее число пожатых рук обязательно четно, ибо в каждом рукопожатии участвуют две руки (при этом каждая рука считается столько раз, сколько она участвовала в рукопожатиях). 2. Число нечетных вершин любого графа четно. 3. Во всяком графе с n вершинами, где n ³2, всегда найдутся, по меньшей мере, две вершины с одинаковыми степенями. 4. Если в графе с вершинами n>2 две вершины имеют одинаковую степень, то в этом графе всегда найдется либо одна вершина степени 0, либо одна вершина степени n - 1. Два графа G1=(V1,E1) и G2=(V2,E2) называются изоморфными, если между их вершинами существует взаимно однозначное соответствие. Алгоритм распознавания изоморфизма двух графов G 1 (X, E)и G 2 (Y, E) 1. Если X ≠ Y, то графы не изоморфны. 2. Выписываем все элементы обоих графов, определяя пары (xi,xj) и (yi, yj) для каждого элемента, где xi, yi - число исходов для каждой вершины обоих графов, а xj, yj – число заходов. 3. Для каждого элемента x графа G1 ищем такой элемент y графа G2, что выполняется условие: число исходов x совпадает с числом исходов y, и число заходов x совпадает с числом заходов y. Найденные элементы x и y соединяем дугой, т.е. строим граф соответствия. Если соответствия нет, то графы неизоморфны. 4. Выписываем подстановку, которая переводит граф G1 в граф G2.
Примеры выполнения заданий 1.
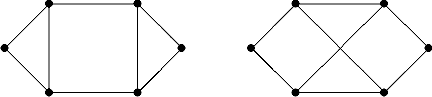
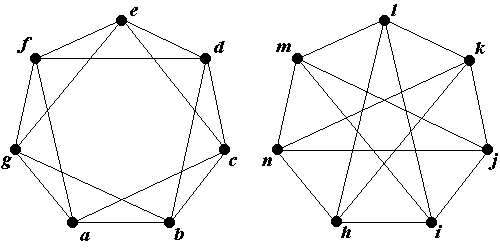
А Б Решение: А) d(v1)=2,d(v2)=3,d(v3)=3,d(v4)=2,d(v5)=3,d(v6)=3. Б) d(v1)=2,d(v2)=3,d(v3)=3,d(v4)=2,d(v5)=3,d(v6)=3. 2. Докажите, что графы G 1 (X 1, E 1) и G 2 (Y 2, E 2) изоморфны.
Решение:
В результате получим подстановку:
Следовательно, графы G1(X, E) и G2(Y, E) изоморфны.
3. Решите задачу по вычислению валентности вершин графа Школьник сказал своему приятелю: - У нас в классе 35 человек. Каждый из них дружит ровно с 11 одноклассниками... - Не может этого быть, - сразу ответил приятель, победитель математической олимпиады. Почему он так решил? Решение: представим себе, что между каждыми двумя друзьями протянута ниточка. Тогда каждый из 35 учеников будет держать в руке 11 концов ниточек, и значит, всего у протянутых ниточек будет 11
4. Решите задачу по выявлению связности компонент графа В компании из 7 мальчиков каждый имеет среди остальных не менее трех братьев. Докажите, что все семеро — братья. Решение: возьмём любых двух мальчиков из этой компании. Предположим, что они не братья. Тогда каждый из них имеет среди оставшихся по три брата. По принципу Дирихле[1], у них есть общий брат, а значит, они братья. Итак, любые два мальчика из этой компании - братья, что и требовалось доказать.
5. Докажите, что граф с n вершинами, степень каждой из которых не менее (n - 1)/2, - связен. Решение: рассмотрим две произвольных вершины и предположим, что они не соединены путем, то есть такой последовательностью ребер, в которой начало очередного ребра, совпадает с концом предыдущего. Каждая из этих двух вершин по условию соединена не менее, чем с (n - 1)/2 другими; при этом все упомянутые вершины различны - ведь если какие-то две из них совпадают, то есть путь, соединяющий исходные вершины. Таким образом, мы указали не менее (n - 1)/2 + (n - 1)/2 + 2 = n + 1 вершин. Противоречие.
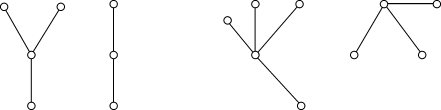
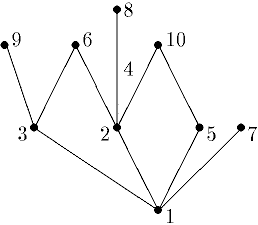
6.Определите, являются ли данные графы деревьями:
Ответ: да, все указанные графы являются деревьями согласно свойствам деревьев. Задания для самостоятельного выполнения
1. Докажите, что валентности вершин графов А и Б совпадают.
А Б 2. Заданы два графа G1(V1, E1) и G2(V2, E2). Выясните, изоморфны ли графы?
2. Определите виды графов и подсчитайте валентность вершин:
4.Определите виды графов и подсчитайте валентность вершин:
Практическое занятие №11. Способы задания графов
Элементы теории Неориентированный граф G (V, E) – непустое конечное множество узлов (вершин) V и набор неупорядоченных пар вершин (ребер) E.
Способы задания графа:
1) аналитический (в виде алгебраической системы); 2) геометрический (в виде произвольного рисунка); 3) матричный (в виде матриц смежности и инцидентности). Пусть v1, v2,... vn - вершины графа G (V, E), а e1, e2,... em - его ребра. Матрицей смежности неориентированного графа G называется матрица A(G) = ||aij||, i=1,...,n; j = 1,..., n, у которой элемент aij равен числу ребер, соединяющих вершины vi и vj (соответственно, идущих из вершины vi в вершину vj).
Свойства матрицы смежности: 1) симметричная относительно главной диагонали, 2) значениями являются натуральные числа и ноль, 3) количество петель записывается на главной диагонали, 4) сумма значений по строке или в столбце равна валентности вершины. Матрицей инцидентности для неориентированного графа с n вершинами и m ребрами называется матрица В(G) = [bij], i=1, 2,..., n, j = 1,2,..., m, строки которой соответствуют вершинам, а столбцы - ребрам. Элемент bij=1, если вершина vi инцидентна ребру ej и bij=0, если вершина vi не инцидентна ребру ej.
Свойства матрицы инцидентности: 1) несимметричная, 2) значениями являются ноль и единица, 3) сумма значений по строке или в столбце равна 2, если нет петель.
Примеры выполнения заданий
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 614; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.229.216 (0.011 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

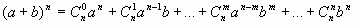
 )4;
)4;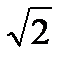 )4;
)4;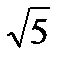 + 2y) 4;
+ 2y) 4;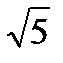 )4;
)4;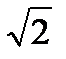 )4;
)4;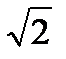 + 4y) 4;
+ 4y) 4;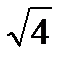 )4;
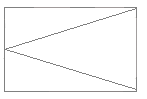
)4;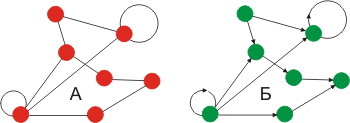 Рис. 2. Примеры А) неориентированного и Б) ориентированного графов.
Рис. 2. Примеры А) неориентированного и Б) ориентированного графов.
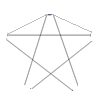
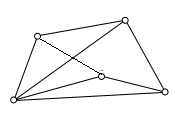 Рис. 5. Пример непланарного графа
Рис. 5. Пример непланарного графа
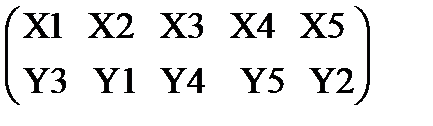
 35 = 385 концов. Но общее число не может быть нечётным, так как у каждой ниточки 2 конца.
35 = 385 концов. Но общее число не может быть нечётным, так как у каждой ниточки 2 конца.