
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электронный практикум по дискретной математикеСодержание книги
Поиск на нашем сайте
Электронный практикум по дискретной математике для бакалавров факультета «Прикладная информатика»
Краснодар-2020 Практические занятия № 1. Множества. Элементы теории Операции над множествами.
Множества можно задавать двумя способами: 1.перечислением элементов множества. Например, множество M={x, y, z} состоит из трёх элементов, порядок перечисления которых не имеет значения, т.е. {x, y, z}={y, x, z}=... 2.описанием элементов множеств: - описанием характеристических свойств, объединяющих элементы в виде уравнений, диаграмм Эйлера-Венна и геометрически. Например, множество M = {x2 Î N; x – простое число} задано квадратами простых чисел. - описанием множеств, порожденных процедурами над элементами, означает указание алгоритма порождения элементов этого множества. Например, подмножество М всех нечетных натуральных чисел с помощью порождающей процедуры имеет вид: M={xÎN: x=1+2n, nÎN} Операции над множествами
n(А î þ В î þ С)= n(А)+ n(В)+ n(С)- n(А ∩ В)-n(А ∩ С)-n(В ∩ С)-n(А ∩ В ∩ С)
где n(Z) – количество элементов множества Z, т.е. его мощность.
Примеры выполнения заданий 1. Заданы множества: А = {1, 3, 5, 7, 9}, B = {1, 2, 3, 4, 5}. Найдите элементы множеств: Д = Аîþ В и Е = АìüВ. Д= {1, 2, 3, 4, 5, 6, 7,8, 9}, Е = {1, 3, 5}.
Задания для самостоятельного выполнения 1. Задайте множество А перечислением его элементов:
2. Заданы множества: А = {1, 3, 9, 10, 8}, B = {5, 3, 11, 4, 8} и
3. Пусть (x, y) - координаты точек плоскости. Укажите штриховкой множеств a A ì ü B и A î þ B:
Практические занятия № 3,4.
Элементы теории Рассмотрим множества Для решения указанной задачи можно использовать таблицы вхождения элементов в множества. Рассмотрим общий принцип построения таких таблиц. Пусть элемент
Заполним следующую таблицу:
Возможны четыре случая: 1.
Здесь 0 означает, что элемент а не принадлежит множеству, соответствующему данному столбцу. 2. 3. 4. Соответствующим образом заполним 2,3 и 4 строки рассматриваемой таблицы.
В результате построена таблица вхождения элементов в множества для множества
Построим таблицы вхождения элементов в множества и соответствующие им диаграммы Эйлера для пересечения множеств
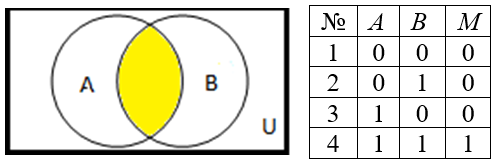
для разности множеств
для симметрической разности множеств
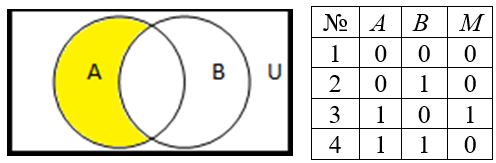
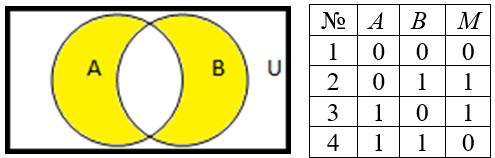
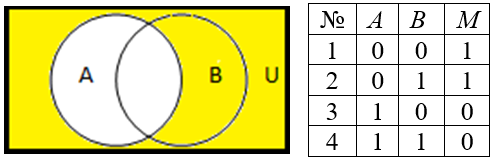
для дополнения множества
Примеры решения задач. Пример 1. Построить таблицы вхождения элементов множества Решение. Так как в данной задаче рассматривается операция над тремя множествами, поэтому в формируемой таблице будет 8 строк.
В данной таблице необходимо учитывать, принадлежит ли произвольный элемент Заполним столбец таблицы для первого действия
Например, в строке 3 имеем элементы 0 1 1, т.е. Далее заполним столбец
По таблице строим диаграмму Эйлера Венна для формулы Укажем область на диаграмме Эйлера, соответствующую строке 3 для которой
Подобным образом нанесем на диаграмму Эйлера номера строк для остальных областей.
Далее закрасим желтым цветом области на диаграмме, которым соответствует значение 1 в последнем столбце
получим диаграмму (области для строк 3,5,7)
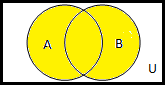
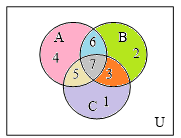
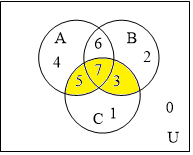
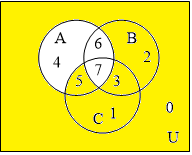
Пример 2. Построить таблицы вхождения элементов в множества для заданного множества и изобразить его на диаграммах Эйлера-Венна: Решение. С учетом порядка действий в формуле M=
Составим диаграмму Эйлера с отмеченными областями.
Закрасим на данной диаграмме необходимые области желтым цветом согласно единичным значениям в таблице вхождения элементов в множества.
получим диаграмму (строки 0,1,2,3,5)
Пример 2.3. Даны множества
Изобразить на числовой прямой следующее множество: Решение. Изобразим на числовой прямой множества U, A, B,
Ответ: [2,5].
Пример 2.4. Даны множества
Изобразить на числовой прямой следующее множество: Решение. Ответ: (-3,4] È(5,6). Пример 2.5. Даны множества
Найти и изобразить на числовой прямой следующее множество: Решение.
Ответ:
Пример 2.6. Даны множества
Найти и изобразить на числовой прямой следующее множество: Решение Ответ: Задания для самостоятельного выполнения
Задание.1. Построить таблицы вхождения элементов в множества для заданных множеств и изобразить их на диаграммах Эйлера-Венна.
Задание 2. Даны множества
Изобразить на числовой прямой следующие множества:
Задание 3. Даны множества
Найти и изобразить на числовой прямой множества:
Практическое занятие № 5. Операции
Элементы теории
Примеры выполнения заданий
1. Докажите тождество: Решение.
Задания для самостоятельного выполнения 1. Изобразите с помощью диаграмм Эйлера-Венна в двух вариантах расположения следующие множества:
б)
Задания для самостоятельного выполнения
1. Проверить, верны ли тождества:
Элементы теории
Пусть X и Y - два множества. Если каждому элементу x множества X поставлен в соответствие некоторый элемент f(x) множества Y, то говорят, что задано отображение f из множества X в множество Y. Обозначение: f: X ® Y. При этом, если f(x) = y, то элемент y называется образом элемента x при отображении f, а элемент x называется прообразом элемента y при обратном отображении f -1.
Отображение f: X ® Y является сюръективным, если каждый элемент yÎY имеет хотя бы один прообраз.
Отображение f: X ® Y называется инъективным, если для любого элемента yÎY существует не более одного прообраза. Если отображение f сюръективно и инъективно одновременно, то оно называется биективным (взаимно однозначным соответствием).
Пусть f: X ® Y и g: Y ® Z - два отображения. Зададим правило h, применение которого к элементу x из X состоит в том, что мы применяем к x правило f, затем к результату f(x) применяем второе правило g, получая в итоге g(f(x)). То есть h(x) = g(f(x)). Полученное отображение h: X ® Z называют композицией отображений g и f и обозначают h = g ° f. Тогда g ° f(x) = g(f(x)). Декартово произведение двух множеств А и В - множество упорядоченных пар <a, b> таких, что aÎA и bÎB. Мощность декартова произведения равна произведению мощностей исходных множеств. Бинарное отношение множеств А и В - подмножество декартового произведения А на В. Область определения отношения (левая область отношения) - множество всех первых элементов пар отношения. Область значений отношения (правая область отношения) - множество всех вторых элементов пар отношения.
Рефлексивное отношение на множестве А - отношение, которое справедливо для каждого элемента множества А как отношение этого элемента к самому себе. Например =, ³ - рефлексивные, ¹, > - нерефлексивные. Симметричное отношение - отношение, результат которого не меняется при перестановке операндов. Транзитивное отношение на множестве А - такое отношение, из справедливости которого для первого и второго операнда и справедливости для второго и третьего операнда следует справедливость этого отношения для первого и третьего операндов, при условии, что все операнды являются любыми элементами множества А. Отношение эквивалентности - отношение, являющееся одновременно рефлексивным, симметричным и транзитивным. Класс эквивалентности R - набор элементов множества, для которых эквивалентное отношение R будет давать одинаковый результат.
Примеры выполнения заданий
2. Выясните, к какому типу относится заданное отображение f: A = {a, b, c}; B = {2, 4, 6, 8}; f: a ® 2; b ® 4; b ® 6; c ® 8; Решение: находим образы: y = f (x): f (a) = 2; f (b) = {4, 6}; f (c) =8 Находим прообразы: x = f --1 (y): f -1 (2) = a; f -1 (4) = b; f -1 (6) = b; f -1 (8) = c; Все элементы В имеют прообразы, значит f – сюрьективно. Т.к элементы 4 и 6 имеют равные прообразы, то f – неинъективно, Следовательно, заданное отображение не является биективным. 3. Пусть f: {1,2,3,5} ® {0,1,2}, g: {0,1,2} ® {3,7,9,13}, h: {3,7,9,13} ® {1,2,3,5} – отображения, показанные на рисунке:
Нарисуйте композиции отображений:
а) g(f); б) h(g); в) h(f (g));
Решение:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 199; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.190.88 (0.014 с.) |

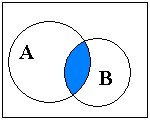
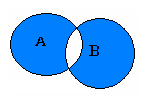
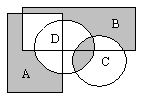
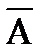 Симметрической разностью двух множеств А и В называется множество
Симметрической разностью двух множеств А и В называется множество

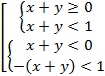 Û
Û 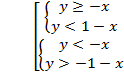
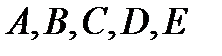 , про которые известно, что они являются подмножествами некоторого универсального множества
, про которые известно, что они являются подмножествами некоторого универсального множества 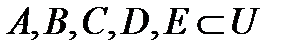 . Необходимо определить элементы некоторого множества М, про которое известно, что оно получено как результат выполнения определенного конечного числа операций над заданными множествами.
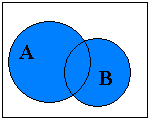
. Необходимо определить элементы некоторого множества М, про которое известно, что оно получено как результат выполнения определенного конечного числа операций над заданными множествами.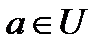 , рассмотрим множество объединение множествА,В
, рассмотрим множество объединение множествА,В 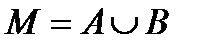 .
.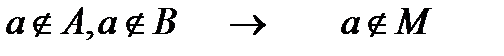 Для этого случая заполним первую строку таблицы
Для этого случая заполним первую строку таблицы
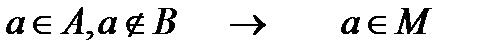
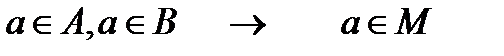
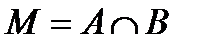
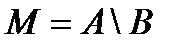
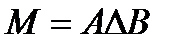
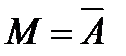
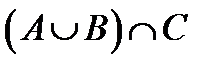 и изобразить его на диаграммах Эйлера-Венна.
и изобразить его на диаграммах Эйлера-Венна.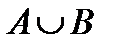
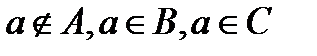 и согласно таблице для
и согласно таблице для 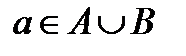 ), ставим значение 1 в столбец
), ставим значение 1 в столбец 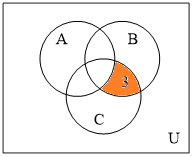
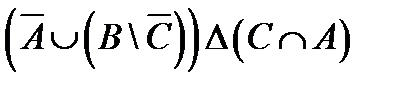 .
.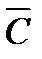
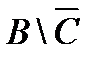
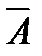
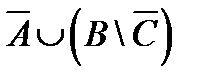
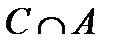
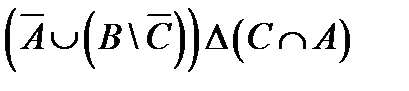
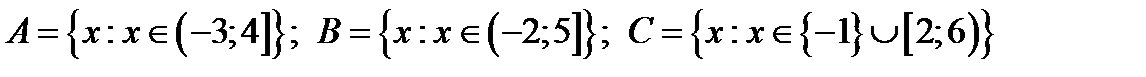 ;
;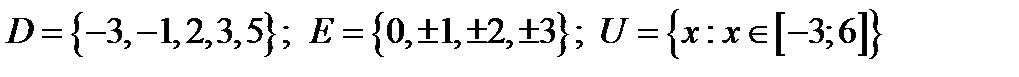 .
.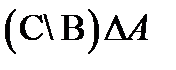 .
.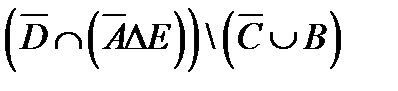 .
.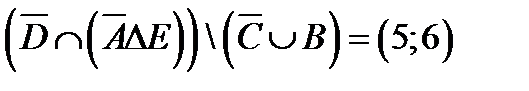
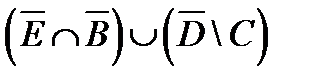 .
.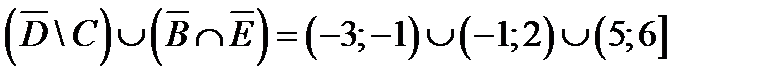
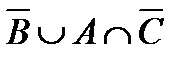
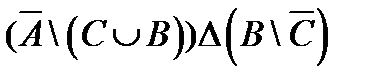
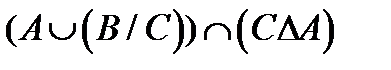
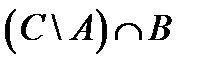
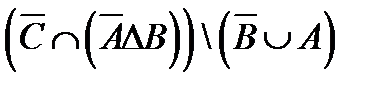
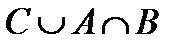

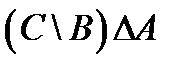
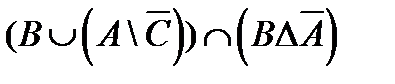
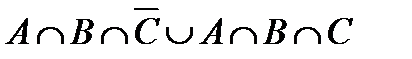
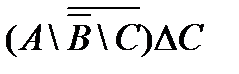
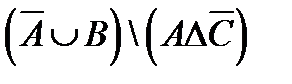
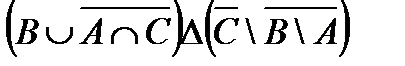
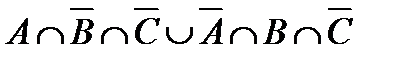
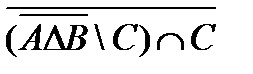
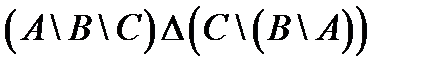
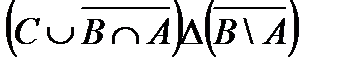
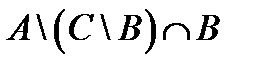
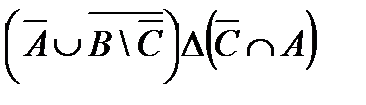
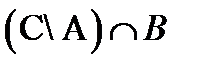
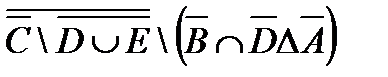
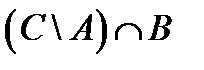
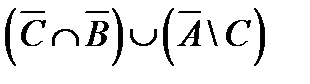
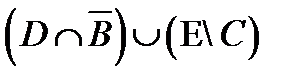
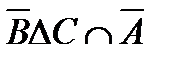
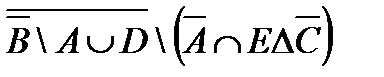
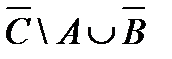
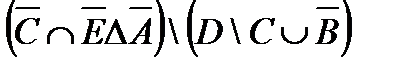
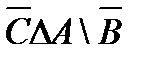
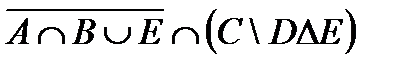
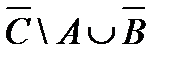
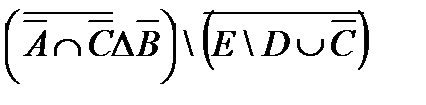
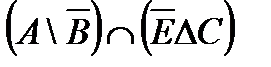
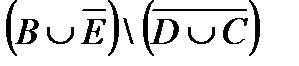
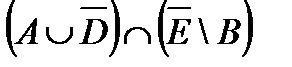
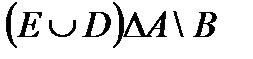
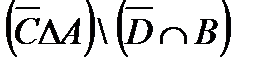

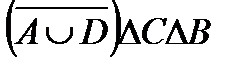
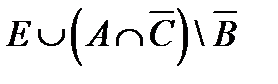
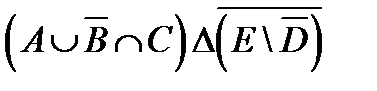
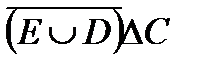
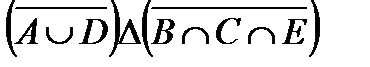
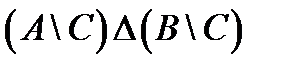
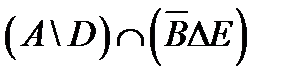
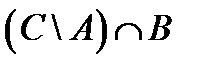
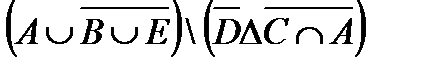
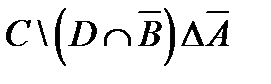
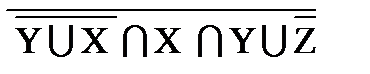 º Z
º Z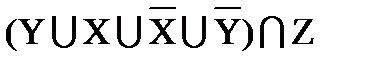 º U ìü Z º Z
º U ìü Z º Z ;
б)
;
б) 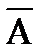 ìü B½C;
ìü B½C;
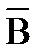 ;
б) (А½В)îþC;
;
б) (А½В)îþC;
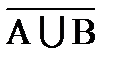 ìüС;
ìüС;
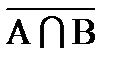 ½С;
½С;
 ;
б) CìüА½
;
б) CìüА½ 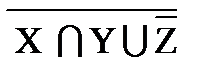 º Z ∪ X
º Z ∪ X
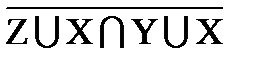 º
º 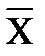 ∩
∩ 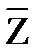 X ∩
X ∩ 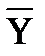 ∪ Z |
∪ Z | 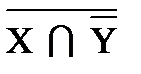 ∪ Z) º Æ;
∪ Z) º Æ;
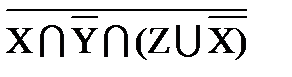 º Y ∪
º Y ∪ 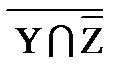 ∪
∪ 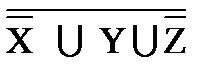 ºX∪Z∪
ºX∪Z∪ 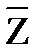 ∩
∩ 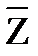 º Æ;
º Æ;
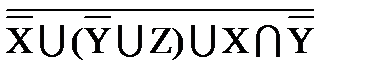 º X ∩
º X ∩  ) |
) | 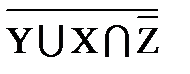 º
º 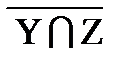 |
| 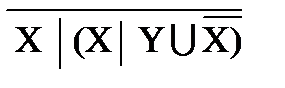 º Æ;
º Æ;
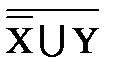 º X ∩
º X ∩ 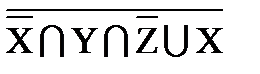 º (
º (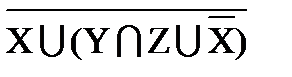 º Æ;
º Æ;
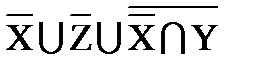 º U
º U
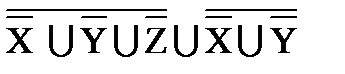 º X ∩ Y
º X ∩ Y
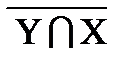 º X ∩
º X ∩  º
º 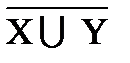 |
| 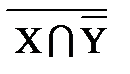 ∪ X ∩ Z º U
∪ X ∩ Z º U
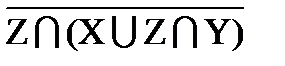 ∪
∪ 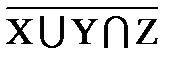 |
| 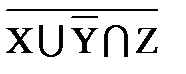 ∩
∩ 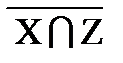 º (Y ∪
º (Y ∪ 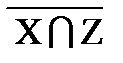 |
| 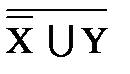 ∩
∩ 


