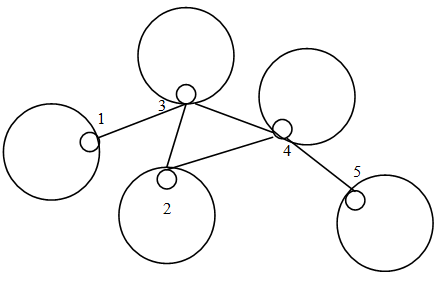
Граф G (V, E): задан геометрически.
а) Задайте граф G (V, E) как алгебраическую систему.
б) Выясните, является ли заданное отношение отношением эквивалентности
Решение:
а) V ={1,2,3,4,},
E ={(1,1),(1,2),(2.2),(2,1),(3,3),(3,4),(4,3),(1,4),(4,4),(4,1),(4,5),(5,4),(5,5)
б) Нарушено условие транзитивности.
Отсутствуют пары (2,4), (4,2), (2,3), (3,2), (3,5),(5,3), (2,5), (5,2), (1,5), (5,1), поэтому отношение R не является эквивалентным.
3. Графы G 1 (V 1, E 1) и G 2 (V 2, E 2) заданы геометрически.
Постройте:
а) для графа G 1 (V 1, E 1) матрицу смежности,
б) для графа G 2 (V 2, E 2) матрицу смежности и матрицу инцидентности.
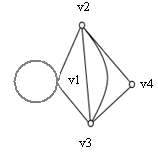 Решение:
Матрица смежности:
v1 v2 v3 v4
А(G) =
Решение:
Матрица смежности:
v1 v2 v3 v4
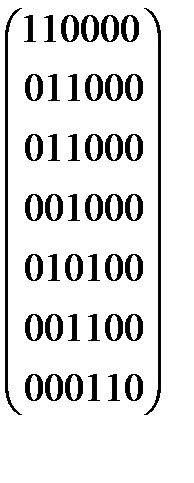
А(G) = 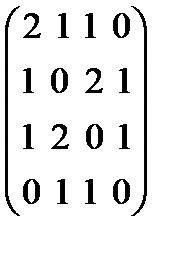
|
e1 e2 e3
e5 e3 e6
e7
Решение: Матрицы смежности и инциденций: 123456 123456 А(G) = |
Ориентированные графы
Ориентированный граф ( или орграф) G1 (V, E) – непустое конечное множество узлов (вершин) V и набор упорядоченных пар вершин (дуг) E.
Пусть v1, v2,... vn - вершины графа G1(V, E), а e1, e2,... em - его дуги.
Матрицей смежности ориентированного графа G1 называется матрица A(G1) = ||aij||, i=1,...,n; j = 1,..., n, у которой элемент aij равен числу дуг, соединяющих вершины vi и vj (соответственно, идущих из вершины vi в вершину vj).
Свойства матрицы смежности:
1) несимметричная, в общем случае, относительно главной диагонали,
2) значениями являются натуральные числа и ноль,
3) количество петель записывается на главной диагонали,
4) сумма значений по строке (столбце) равна валентности вершины.
Матрицей инцидентности для ориентированного графа с n вершинами и m дугами называется матрица В(G1) = [bij], i=1, 2,..., n, j = 1,2,..., m, строки которой соответствуют вершинам, а столбцы - дугам. Ее элемент: bij=1, если дуга еi выходит из вершины vj; bij= -1, если дуга ei входит в вершины vj; bij=0, если вершина vj не инцидентна дуге еi.
Свойства матрицы инцидентности:
1) несимметричная, 2) значениями являются -1, ноль и 1.
Примеры выполнения заданий
1. Орграф G 1 (V, E) задан геометрически. Постройте для орграфа:
а) матрицу смежности; б) матрицу инцидентности.
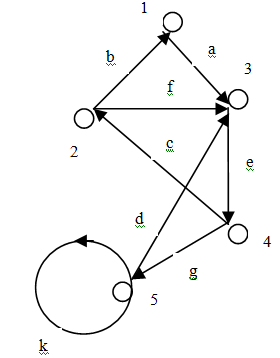
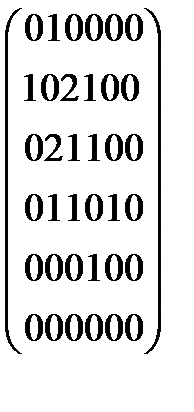
| Решение а): матрица смежности А(G1)=
|
Решение б):
матрица инцидентности В(G1)=
| a | b | c | d | e | g | f | k | |
| 1 | 1 | -1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | -1 | 0 | 0 | 0 | 1 | 0 |
| 3 | -1 | 0 | 0 | -1 | 1 | 0 | -1 | 0 |
| 4 | 0 | 0 | 1 | 0 | -1 | 1 | 0 | 0 |
| 5 | 0 | 0 | 0 | 1 | 0 | -1 | 0 | 0 |
2. Решите следующую задачу по обходу графов:
В некоторой стране есть столица и еще 100 городов. Некоторые города (в том числе и столица) соединены дорогами с односторонним движением. Из каждого нестоличного города выходит 20 дорог, и в каждый такой город входит 21 дорога. Докажите, что в столицу нельзя проехать ни из одного города.
Решение:
Пусть в столицу входит a дорог. Тогда общее число "входящих" дорог равно 21 · 100 + a, а общее количество "выходящих" дорог не больше 20 · 100 + (100-a). Поэтому 21×100 + а £ 20×100 + (100 – а), то есть 2а £ 0. Таким образом, a = 0.
Задания для самостоятельного выполнения
|
| Поделиться: |



 В(G) =
В(G) =