Высоты, медианы, биссектрисы и средние линии треугольника

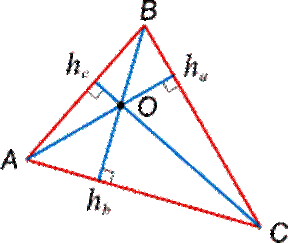
Кроме основных элементов в треугольнике рассматривают и другие отрезки, обладающие интересными свойствами: высоты, медианы, биссектрисы и средние линии.

Высота

 

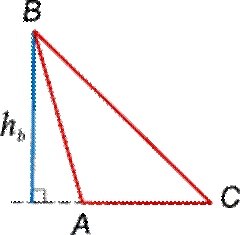
Высоты треугольника – это перпендикуляры, опущенные из вершин треугольника на противоположные стороны.

Для построения высоты необходимо выполнить следующие действия:

1) провести прямую, содержащую одну из сторон треугольника (в случае, если проводится высота из вершины острого угла в тупоугольном треугольнике);

2) из вершины, лежащей напротив проведенной прямой, провести отрезок из точки к этой прямой, составляющий с ней угол 90 градусов.

 

 

Рис. 2.

 

Точка пересечения высоты со стороной треугольника называется основанием высоты (см. рис. 2).

Свойства высот треугольника

1. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному треугольнику.

2. В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.

3. Если треугольник остроугольный, то все основания высот принадлежат сторонам треугольника, а у тупоугольного треугольника две высоты попадают на продолжение сторон.

4. Три высоты в остроугольном треугольнике пересекаются в одной точке и эту точку называют ортоцентром треугольника.

 

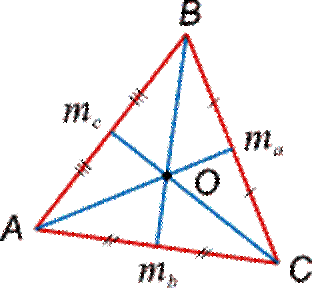
Медиана

Медианы (от лат. mediana– «средняя») – это отрезки, соединяющие вершины треугольника с серединами противолежащих сторон (см. рис. 3).

Для построения медианы необходимо выполнить следующие действия:

1) найти середину стороны;

2)соединить точку, являющуюся серединой стороны треугольника, с противолежащей вершиной отрезком.

 

Рис. 3.

Свойства медиан треугольника

1. Медиана разбивает треугольник на два треугольника одинаковой площади.

2. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.

Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.

Биссектриса

Биссектрисами (от лат. bis – дважды» и seko – рассекаю) называют заключенные внутри треугольника отрезки прямых, которые делят пополам его углы (см. рис. 4).

Для построения биссектрисы необходимо выполнить следующие действия:

1) построить луч, выходящий из вершины угла и делящий его на две равные части (биссектрису угла);

2) найти точку пересечения биссектрисы угла треугольника с противоположной стороной;

3) выделить отрезок, соединяющий вершину треугольника с точкой пересечения на противоположной стороне.

 

 

Рис. 4.

Свойства биссектрис треугольника

1. Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон.

2. Биссектрисы внутренних углов треугольника пересекаются в одной точке. Это точка называется центром вписанной окружности.

3. Биссектрисы внутреннего и внешнего углов перпендикулярны.

4. Если биссектриса внешнего угла треугольника пересекает продолжение противолежащей стороны, то ADBD=ACBC.

5. Биссектрисы одного внутреннего и двух внешних углов треугольника пересекаются в одной точке. Эта точка — центр одной из трех вневписанных окружностей этого треугольника.

6. Основания биссектрис двух внутренних и одного внешнего углов треугольника лежат на одной прямой, если биссектриса внешнего угла не параллельна противоположной стороне треугольника.

7. Если биссектрисы внешних углов треугольника не параллельны противоположным сторонам, то их основания лежат на одной прямой.

 

Средняя линия

Средние линии - это отрезки, соединяющие середины двух сторон.

Для построения средней линии необходимо выполнить следующие действия:

1) найти середины двух сторон треугольника;

2) соединить середины сторон отрезком (см. рис.5).

 

Рис. 5.

 

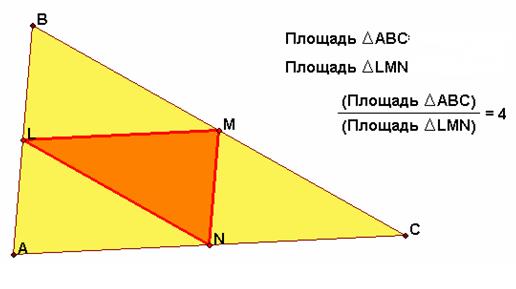
Три средние линии треугольника образуют «вписанный» в него треугольник, называемый серединным. Его площадь в четыре раза меньше площади данного треугольника (см. рис.6).

 

Рис. 6.

 

 

ВИДЫ ТРЕУГОЛЬНИКОВ

 

Существует две классификации треугольников: по углам (см. рис. 7) и сторонам (см. рис. 8) (2, стр. 534).

 

Классификация по углам

Определение. Треугольник называется остроугольным, если все три его

угла — острые, то есть меньше 90°.

 

Определение. Треугольник называется тупоугольным, если один из его

углов — тупой, то есть больше 90°.

Определение. Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой, две другие стороны называются катетами.

 

Рис. 7.

Классификация по сторонам

 

Рис. 8.

 

Определение. Треугольник называется равнобедренным, если у него две стороны равны. Эти равные стороны называются боковыми сторонами, а третья сторона называется основанием треугольника.

 

Определение. Треугольник, у которого все стороны равны, называется равносторонним или правильным.

РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК

 

Определение. Равнобедренный треугольник — треугольник, в котором две стороны равны между собой. По определению, правильный треугольник также является равнобедренным, но обратное, вообще говоря, неверно (см. рис. 9).