
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проекция вектора на координационную ось равна разности координат конца и начала вектора.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
S - вектор перемещения материальной точки Sx - проекция вектора S на ось ОХ Sy - проекция вектора S на ось OY Рис.9. Проекция вектора на ось Рассмотрим примеры расположения векторов относительно оси ОХ (аналогично ось OY): проекция «+», если S х 1 > S х0; угол острый (α <900); проекция «-», если S х 1 < S х0; угол тупой (β > 900); проекция = точке, если S х 1 = S х0; угол развернутый (γ =1800). Обратить внимание на обозначения: S - вектор перемещения материальной точки; S - модуль вектора; S х - проекция вектора на ось (ОХ) Выводы для векторов, расположенных в одной плоскости: 1.Если вектор параллелен и сонаправлен оси, то его проекция совпадает с модулем вектора: S х= S, если проекция имеет противоположное направление оси, то S х=- S, если вектор перпендикулярен оси, то S х=0 2.Модуль вектора не может быть «-», он всегда ≥ 0; проекция вектора может быть отрицательной, если угол между вектором и осью > 900; вектор не может быть «+» или «-», так как это не скалярная величина и имеет только направление. Противоположные векторы имеют равные модули, но разное направление
Рис.10. Примеры связи направления вектора и модуля Связь модуля и направления вектора с его проекцией Математическая справка Теорема Пифагора. Квадрат гипотенузы в прямоугольном треугольнике равен сумме квадратов катетов. Терема синусов.
ах- прилежащий катет; а y -противолежащий катет, α - угол между вектором аи осью ОХ Рис. 11. Связь между модулем вектора и его проекция ми на оси ОХ и ОУ Определение нахождения точки
Координаты точки Формулы приведения
Синусы и косинусы углов (х- синус, у- косинус)
Задача. Катер прошел по озеру в направлении на С-В 2 км, а затем на север 1 км. Найти модуль и направление движения. Дано: Решение: S 1 = 2 км на С-В Пусть масштаб в 1 см 1 км
Модуль и направление С
Ю
Выбираем систему координат ХОУ, поместив е центр О в исходную точку, из которой катер отправился в плавание, т.о. ось ОХ совпадает с направлением на В, ось ОУ- на С. т.о.: Вектор S 1 соответствует перемещению катера до поворота (С-В направление), S 2 - перемещению на север. 1. Способ: замеряем линейкой суммирующий вектор S = 2,8 см- 2,8 км. Угол замеряем транспортиром 59 0 2. Способ (геометрический - аналитический):
tg α/ = Sx/Sy=2.41/1.41=1.71 α=59.7 Виды движения. Равномерное прямолинейное движение (РПД) Механическое движение – изменение положения тела в пространстве в ЛЮБОЙ момент времени относительно системы отсчета. х(t)= x 0 + Sx (t) y (t)= y 0 + Sy (t) Определение 12 Равномерное прямолинейное движение –движение, при котором тело за любые равные промежутки времени совершает равные перемещения. Т.е. движение с постоянной скоростью.
1 ед. Определение 13 Скорость V→ − векторная величина, характеризующая направление и быстроту перемещения материальной точки: .V→=ΔS→/Δt. В проекции на ось x: Vx=Δx/Δt. В СИ единица измерения скорости − метр/секунду: мc[V]=м/c. На практике зачастую используются внесистемные единицы измерения скорости. Например, кмчкм/ч. Следует знать, что в мс1 м/с содержится 3,6 км/ч. Скорость может изменяться во времени. Мгновенная скорость − скорость в данный момент времени в данной точке траектории. В любой точке криволинейной траектории она направлена по касательной к траектории в этой точке. Обычно под скоростью понимают именно мгновенную скорость, т. е. скорость в определенный момент времени. Часто для упрощения описания неравномерного движения используют среднюю путевую скорость. Средняя путевая скорость − скалярная величина Vср=L/t, где L – весь путь, t – все время движения (как правило, включая остановки).
При решении задач на среднюю скорость важно на рисунке или в комментариях к решению определить те величины, которые вы вводите для промежуточных выкладок. Следует избегать ранней подстановки численных значений известных величин, прежде чем из уравнения выражена искомая величина. Пример: Путешественник треть пути двигался со скоростью 1 км/ч, а оставшийся участок – со скоростью 4 км/ч. Какова его средняя скорость на всем пути? Дано: Решение v1=1 км/ч, Пусть 3S – весь путь. Участок S пройден за время t1=S/v1, ос- v2=4 км/ч, тавшийся участок в течение времени t2=2S/v2.Все время в пу- vср-? ти t1+t2. vср=2 км/ч. Прямолинейное равномерное движение − движение по прямой, при котором за любые равные промежутки времени тело совершает равные перемещения. При таком движении скорость V→ тела не изменяется. Расстояние S, которое за время t проходит тело, связано с величиной скорости V формулой: . S = v * t величины, описывающие это движение: скорость V→, перемещение S→, время t. Уравнение скорости: V→=V0→=const→. При таком движении скорость V→ тела не изменяется. Уравнение перемещения: S→=V→t. Расстояние S, которое за время t проходит тело, связано с величиной скорости V формулой: S=vt Уравнение скорости: v→=v0→=const→, в проекции на ось x: vx=v0x=const. При таком движении скорость v→ точки не изменяется. Уравнение перемещения: S→=v0→t, в проекции на ось x: Sx= vxt. При таком движении перемещение S→ точки изменяется лине йно со временем. Координатное уравнение: x=x0+vxt. Для координат вдоль других осей формула выглядит аналогично.
|
||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 513; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.253.195 (0.009 с.) |


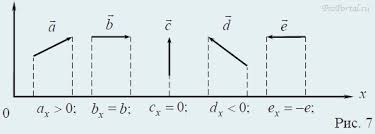
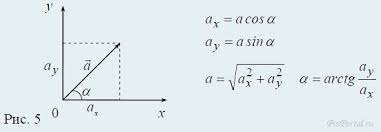
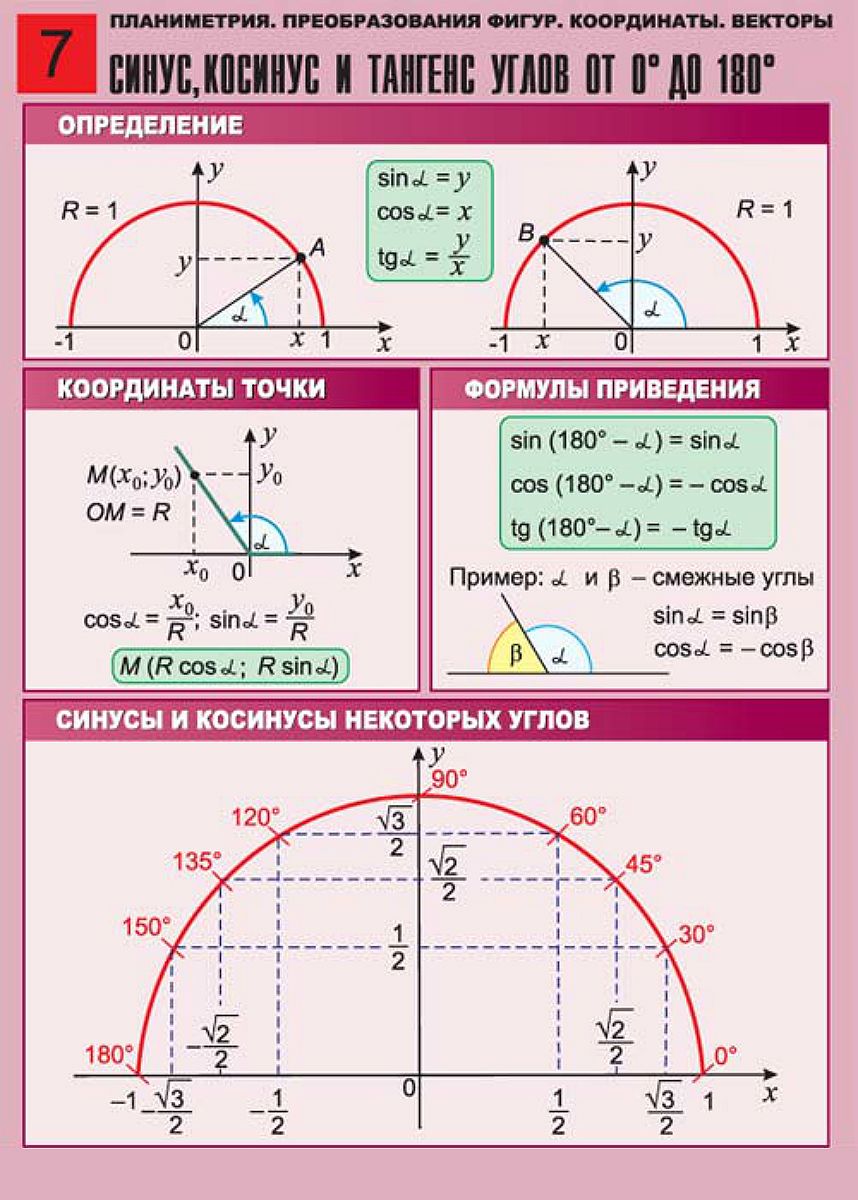
 S 2 = 1 км на С Зададим на плоскости направление Ю- С
S 2 = 1 км на С Зададим на плоскости направление Ю- С


