
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальное уравнение изогнутой упругой линии балкиСодержание книги
Поиск на нашем сайте
Пусть к консоли бруса приложена сила F (рис. 2.25); форму его изогнутой оси (или упругой линии) можно определить при помощи выражения для радиуса кривизны:
Известно, в неподвижной системе координат zy кривизна кривой связана с производными функции y следующей зависимостью:
Мы рассматриваем весьма жесткие брусья, поэтому y ′, равная tg a, величина небольшая. Например, a = 5°, tg 5° = 0,0875, (tg 5°)2 = 0,00765. Такая величина пренебрежимо мала по сравнению с 1. Поэтому можем принять 1/ρ» y ². Тогда y ² — это кривизна изогнутой оси бруса, y ′ — тангенс угла наклона касательной к упругой линии бруса (в силу малости угла можно считать, что y ′ — это угол a, на который повернется сечение), y = f (z) — прогиб упругой линии. Итак,
Перепишем полученную зависимость, уточнив, что изгибающий момент М изг приложен в плоскости zy:
или
Полученное выражение представляет собой дифференциальное уравнение изогнутой оси балки (упругой линии балки). Пример 2.14 Для бруса, показанного на рис. 2.26, требуется определить прогиб в точке В и углы поворота опорных сечений. Принять: l = 5 м, q = 800 Н/м, Jx = 166 см4, Е = 2·105 Н/мм2, АВ = l /2.
Решение. 1. Определяем реакции опор
2. Проводим оси координат, выбрав начало отсчета на левой опоре А. 3. Определяем изгибающий момент в произвольном сечении бруса, отстоящем на расстоянии z от левой опоры. Весь пролет бруса представляет собой один участок. Записываем сумму моментов относительно центра тяжести сечения, рассматривая равновесие левой отсеченной части: M изг = YAz - qz 2/2, 0 £ z £ l. 4. Составляем дифференциальное уравнение упругой линии балки:
5. Проинтегрировав, найдем зависимость для определения углов поворота опорных сечений:
При z = 0 y ′ = q A: EJx q A = 0 - 0 + D 1; q A = D 1/(EJx); при z = l y ′ = q C: EJx q C = ql 3/4 - ql 3/4 - ql 3/6 + D 1; q C = (ql 3/12 + D 1)/(EJx). Постоянная интегрирования D 1 после первого интегрирования пока неизвестна. 6. Проинтегрируем еще раз и найдем функцию для определения прогибов: EJxy = (1/12) qlz 3 - (1/24) qz 4 + D 1 z + D 2. В полученную зависимость проставляем граничные условия для определения постоянных интегрирования D 1 и D 2. При z = 0 y = 0: 0 = 0 - 0 + 0 + D 2, отсюда D 2 = 0; при z = l y = 0: 0 = (1/12) ql 4 - (1/24) ql 4 + D 1 l, отсюда D 1 = -(1/24) ql 3. 7. Запишем уравнения для определения угловых перемещений и прогибов сечений балки в окончательном виде:
8. Определяем прогиб в точке В — fB. В уравнение прогибов подставляем координату точки В (z = l /2):
откуда Подставляем исходные данные: l = 5 м = 5000 мм, q = 800 Н/м = 0,8 Н/мм, Jx = = 166 см4 = 166·104 мм4, Е = 2·105 Н/мм2:
Знак «-» означает, что балка прогнулась вниз (положительное направление оси координат y — вверх). 9. Определяем угол поворота опорного сечения q А. В уравнение угловых перемещений подставляем z = 0:
Подставляем исходные данные: l = 5000 мм, q = 0,8 Н/мм, Jx = =166·104 мм4, Е = 2·105 Н/мм2:
Угол получился отрицательный, так как находится в четвертом квадранте. 10. Определяем угол поворота опорного сечения q С. В уравнение угловых перемещений подставляем z = l:
Сечение над опорой С повернулось на такой же угол, как и сечение над опорой А, вследствие симметрии приложенных к балке нагрузок; знак — положительный, так как угол по отношению к оси z острый.
|
||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 231; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.01 с.) |


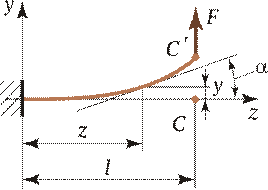 Рис. 2.25
Рис. 2.25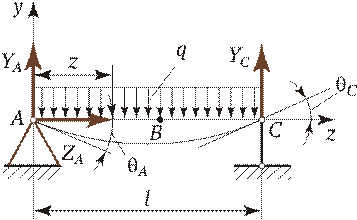 Рис. 2.26
Рис. 2.26


