
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы сопротивления материаловСтр 1 из 16Следующая ⇒
Закон Гука Многочисленные наблюдения за поведением твердых тел показывают, что в подавляющем большинстве случаев перемещения в определенных пределах пропорциональны действующим силам. Впервые в 1676 г. Р. Гуком был сформулирован закон о том, что «какова сила, такова и деформация». В современной трактовке закон Гука определяет линейную зависимость между напряжением и деформацией: s = E e. Здесь коэффициент пропорциональности Е есть модуль упругости первого рода, e — деформация, которую для однородного стержня можно определить как
Величину e иногда называют относительным удлинением стержня длиной l, удлинение которого под действием приложенной силы составило D l. Модуль упругости первого рода является физической константой материала; он определяется экспериментально. Для наиболее часто встречающихся материалов его значения приведены в табл. 2.1. Таблица 2.1. Механические характеристики материалов [11] Удлинение стержня Если в закон Гука вместо напряжения подставить s = N / S, а вместо деформации e = D l / l, то получим выражение для определения удлинения стержня, у которого на длине l внутренняя нормальная сила постоянная и поперечное сечение не изменяется:
При решении многих практических задач возникает необходимость наряду с удлинением, обусловленным напряжением s, учитывать также удлинения, связанные с температурным воздействием. В этом случае деформацию рассматривают как сумму силовой и температурной деформации:
где a — коэффициент температурного расширения материала. Для однородного стержня, нагруженного на концах и равномерно нагретого:
Построение эпюр График изменения нормальной силы, напряжений и перемещений стержня вдоль его оси называется эпюрой соответственно нормальных сил, напряжений и перемещений. Эпюры дают наглядное представление о законах изменения различных исследуемых величин. Построение эпюр рассмотрим на конкретном примере.
Пример 2.1 Для бруса, изображенного на рис. 2.3, а, построить эпюры внутренних сил, напряжений и перемещений по длине бруса.
Решение. 1. Выбираем начало отсчета в неподвижном сечении (точка O); положительное направление оси z направим по оси бруса, т. е. вниз. 2. Определим реакцию, составив одно уравнение равновесия:
Отсюда NО = 2 F. 3. Построим эпюру внутренних сил N. Для этого на расстоянии z 1 рассечем брус и рассмотрим равновесие нижней части (рис. 2.3, б):
Отсюда N 1 = F, что справедливо для l £ z 1 £ 3 l. В этих пределах в брусе возникает растяжение, так как N 1 направлена от сечения. Теперь выберем второй участок бруса 0 ≤ z 2 ≤ l и рассмотрим равновесие верхней части (рис. 2.3, в):
Отсюда N 2 = 2 F. Поскольку N 2 направлена к сечению, то брус под действием сил NO и N 2 сжимается. После того как определили все внутренние нормальные силы, переходим к построению эпюры нормальных сил (рис. 2.3, г). Вправо будем откладывать положительные, а влево — отрицательные значения нормальных сил. Анализируя построенную эпюру N, заметим, что внутренние силы не зависят от размеров поперечного сечения, а зависят только от приложенных внешних сил. Поэтому брус разбивают на участки по числу приложенных на его длине сосредоточенных сил. В данном случае было два участка. При проверке правильности построения эпюры N следует обратить внимание на то, что на эпюре внутренних сил в тех сечениях, где были приложены внешние силы, должны быть скачки, равные приложенной внешней силе. 4. Построим эпюру напряжений s. Брус следует разбить на участки. Поскольку s = N / S, то участков на эпюре будет столько, сколько раз меняется поперечное сечение; при этом следует обращать внимание, чтобы при постоянной площади поперечного сечения нормальная сила на эпюре N оставалась неизменной. С учетом этого на эпюре s будут три различных значения s (рис. 2.3, д): s1 = N 1/ S 1 = F / S; s2 = N 1/ S 2 = F /(2 S); s3 = N 2/ S 2 = -2 F /(2 S) = - F / S.
5. Строим эпюру перемещений U. Начинать следует от неподвижного сечения, т. е. от сечения O. Определим перемещение сечения, находящегося от неподвижного на расстоянии z 2:
Если 0 £ z 2 £ l, то для z 2 = l перемещение
Для l £ z £ 2 l
или Для 2 l £ z 1 £ 3 l
Откладываем вычисленные перемещения на эпюре U (рис. 2.3, е). Диаграмма растяжения Наиболее наглядно особенности диаграммы растяжения можно показать на примере испытания образца из низкоуглеродистой стали (рис. 2.4). Диаграмма вычерчена в координатах F —D l. На кривой можно выделить четыре зоны. Зона ОА носит название зоны упругости. Здесь удлинение образца подчиняется закону Гука и
Зона АВ называется зоной общей текучести, а участок АВ — площадкой текучести. Здесь происходит существенное изменение длины образца без заметного увеличения нагрузки. Не все металлы имеют площадку текучести. Например, у алюминия, отожженной меди, легированных сталей площадка текучести не обнаруживается. Зона ВС называется зоной упрочнения. Здесь удлинение образца сопровождается возрастанием нагрузки. В стадии упрочнения на образце намечается место будущего разрыва и начинает образовываться так называемая шейка — местное сужение образца. При дальнейшем растяжении образца шейка быстро прогрессирует. Начиная с точки С, удлинение образца происходит с уменьшением силы, но среднее напряжение в поперечном сечении шейки возрастает. Удлинение образца носит в этом случае местный характер, поэтому участок СD называется зоной местной текучести. Точка D соответствует разрушению образца. Смятие При сжатии двух тел возникает опасность смятия контактирующих поверхностей. Напряжения, возникающие на контактирующих поверхностях, называются напряжениями смятия. Смятие имеет место, например, в клепаных и болтовых соединениях. Напряжение смятия определяют по формуле
где F — сила, с которой сдавливаются контактирующие поверхности; S см — площадь смятия. Если поверхность смятия является криволинейной, то площадь смятия вычисляется как площадь проекции этой поверхности на плоскость, перпендикулярную к линии действия сминающей силы. Пример 2.4 Проверить прочность клепаного соединения (см. рис. 2.8), если [t]ср = = 100 Н/мм2; [s]см = 240 Н/мм2; [s]р = 140 Н/мм2.
Решение. 1. Проверяем прочность заклепки на срез (методика расчета приведена в примере 2.3). 2. Проверяем на смятие стенки отверстий в соединяемых листах:
Полученное значение фактического напряжения смятия меньше допускаемого, так как по условию [s]см = 240 Н/мм2. Следовательно, смятия стенок отверстий не произойдет. 3. Проверяем прочность листов на растяжение по формуле
Для определения опасного сечения в сложных случаях обычно строят эпюры N, а затем s. В данном случае задача более простая. Ясно, что опасным сечением является сечение А — А. Площадь поперечного сечения каждого листа S = 10·(120 - 2·20) = 800 мм2, а фактическое напряжение
что меньше допускаемого: 62,5 < 140. Ответ. Можно считать, что прочность клепаного соединения достаточна.
Кручение
Под кручением понимается такой вид нагружения, при котором в поперечных сечениях возникает только крутящий момент. Прочие внутренние силовые факторы (нормальная и поперечные силы, изгибающие моменты) равны нулю. Рассмотрим кручение круглого бруса (рис. 2.9). К круглому брусу, жестко заделанному в стенку, на свободном торце приложен крутящий момент М. В результате этого брус деформируется: смежные сечения поворачиваются относительно друг друга, образующая ОВ искривляется и занимает положение ОС. При рассмотрении кручения принимаются следующие допущения и правила:
При кручении в поперечном сечении бруса возникают касательные напряжения (чистый сдвиг). Угол закручивания j и относительный угол закручивания θ связывает следующая зависимость:
q = j/ l. Касательные напряжения t при кручении распределяются в сечении по линейной зависимости: в центре они равны нулю, а на максимальном радиусе поперечного сечения — максимальному значению tmax, по которому ведется расчет. Значение касательного напряжения зависит от внутреннего крутящего момента и геометрической характеристики поперечного сечения: tmax = M кр/ Wр, где Wp — полярный момент сопротивления. Для сплошного поперечного сечения диаметром D Wp = 0,2 D 3; для кольцевого сечения (полый вал) Wp = 0,2 D 3(1 - d 4/ D 4), где d — внутренний диаметр (диаметр отверстия); D — внешний диаметр вала. Покажем, что валы сплошного поперечного сечения использовать неэкономично. Пример 2.5 Вал передает момент M = 10000 Н·м. Требуется подобрать размеры поперечного сечения вала для случаев: а) сплошного кругового сечения и б) кругового сечения с отверстием d = (7/8) D. Сравнить оба сечения по расходу металла. Допускаемое напряжение [t] = 6000 Н/см2. Решение. 1. Определяем требуемый момент сопротивления для обоих поперечных сечений:
2. Определяем диаметр вала сплошного сечения:
3. Определяем диаметр вала полого поперечного сечения:
4. Определяем расход металла. Для этого вычислим площади поперечных сечений сплошного и полого валов: для сплошного вала
для полого вала
Поскольку расход металла будет пропорционален площади поперечного сечения, то полое сечение является более экономичным и в данном случае дает более чем двукратное снижение веса вала. Построение эпюр При кручении, как и при растяжении, строят эпюры внутренних силовых факторов (крутящих моментов), напряжений (tmax) и перемещений (углов закручивания j). Построение эпюры М кр. Всю длину бруса (рис. 2.10) разобьем на два участка. На эпюре внутренних силовых факторов в сечениях, где приложены внешние силы, будут скачки, равные приложенным нагрузкам (в данном случае — внешним скручивающим моментам). Применяя метод сечений с учетом правила знаков для крутящих моментов, строим эпюры М кр. На рис. 2.10 для изображения внешних моментов применено условное обозначение в виде кружков: кружок с точкой обозначает силу, направленную «на себя», а кружок с крестиком — силу, направленную «от себя».
Построение эпюры tmax. Всю длину бруса разбиваем на три участка; на каждом из них М кр и Wр сохраняют постоянное значение. Затем подставляем в формулу tmax = = М кр/ Wр соответствующие значения М кр и Wр: на I участке на II участке на III участке Поскольку все внутренние крутящие моменты положительны, то и все касательные напряжения на эпюре tmax будут также положительны.
Построение эпюры j. Прежде всего необходимо установить зависимость, по которой будем определять углы закручивания j. На основании закона Гука для сдвига запишем выражение для максимального касательного напряжения в поперечном сечении круглого бруса: tmax = G g. Из рис. 2.9 видно, что при кручении образующая цилиндра ОВ поворачивается на угол g и занимает положение ОС. При этом дуга ВС равна g l; с другой стороны, та же дуга ВС равна j r. Следовательно, g l = j r, откуда g = j r / l. Подставляя найденное значение g в закон Гука, получим
С другой стороны, t = M кр/ Wр. Следовательно,
Выразим отсюда угол закручивания Величину Wpr (или WpD /2) называют полярным моментом инерции сечения и обозначают Jp. Таким образом, между моментом сопротивления и полярным моментом инерции бруса круглого поперечного сечения диаметром D существует следующая зависимость:
Полярный момент инерции: для сплошного круглого бруса Jp @ 0,1 D 4; для полого круглого бруса
Запишем выражение для угла закручивания j в виде
Произведение GJp называют жесткостью бруса при кручении. Итак, получена зависимость, по которой можно определять углы закручивания бруса. Определять угол закручивания по этой зависимости можно только при условии, что на длине l все входящие в эту формулу величины М кр, Jp и G — постоянные. Переходим к построению эпюры угловых перемещений. Вал по длине разбиваем на четыре участка. Так же, как и при построении эпюры перемещений при растяжении, начинаем строить эпюру от неподвижного сечения, т. е. от жесткой заделки. В конце I участка угол закручивания
В конце II участка угол закручивания
В конце III участка
На IV участке угол закручивания будет равен углу закручивания jIII, так как на этом участке отсутствуют внутренние крутящие моменты. Вычисленные угловые перемещения откладываем на эпюре j.
Прямой поперечный изгиб
Прямой поперечный изгиб Под изгибом понимается такой вид нагружения, при котором в поперечных сечениях бруса возникают изгибающие моменты (см. подразд. 2.1). Если изгибающий момент является единственным силовым фактором, а поперечные и нормальные силы отсутствуют, то такой изгиб называется чистым. В большинстве случаев в поперечных сечениях бруса наряду с изгибающими моментами возникают поперечные силы. В этом случае изгиб называют поперечным. Брус, работающий в основном на изгиб, называется балкой. На балку могут действовать сосредоточенные силы и моменты, а также распределенные по длине. Например, на рис. 2.17 F — сосредоточенная сила, М — сосредоточенный момент; на участке а приложена распределенная нагрузка от нуля до q max.
Анализ внутренних силовых факторов начинают с определения полной системы внешних сил. Рассмотрим некоторые характерные примеры и установим правила определения изгибающих моментов и поперечных сил. На рис. 2.18, а показана простейшая двухопорная балка, нагруженная силой F. Освобождаем балку от связей и заменяем их действие реакциями. Опора А представляет собой невесомый стержень, поэтому реакция RA пойдет вдоль него. В шарнире В реакцию раскладываем на две составляющие. Несмотря на то, что выбор системы координат, безусловно, произволен, в сопротивлении материалов принято ось z направлять вдоль бруса; оси х и у должны лежать в плоскости, перпендикулярной этой оси, причем поворот от оси х к оси у должен происходить против хода часовой стрелки, если смотреть с конца оси z (рис. 2.18, б). Начало отсчета располагают в центре тяжести поперечного сечения. В этом случае оси х и у будут главными центральными осями поперечного сечения.
Составим уравнения равновесия для плоской системы сил и определим неизвестные реакции связей. Неизвестных величин три — RA, YB, ZB. Уравнений статики тоже три, следовательно, задача статически определимая:
Отсюда находим реакции опор
Теперь приступим к выявлению внутренних силовых факторов в поперечных сечениях бруса. Для этого между точками приложения внешних сил и моментов, применяя метод сечений, мысленно разрезают балку на части (рис. 2.18, в и г) и составляют уравнения равновесия силовых факторов, приложенных к отсеченным частям. Так, в рассматриваемом примере необходимо делать сечения дважды: на расстоянии z 1 и z 2 от левой опоры. На рис. 2.18, в показано сечение бруса на расстоянии z 1 от левой опоры и проставлены внутренние силовые факторы: изгибающий момент М изг и поперечная сила Q. Следует обратить внимание на то, чтобы внутренние силовые факторы в поперечном сечении в левой и правой (см. рис. 2.18, г) частях были обязательно противоположны по направлению. Как уже известно, внутренние силовые факторы определяют из уравнений равновесия сил, приложенных к отсеченным частям. Следует условиться о знаках поперечных сил и моментов. Существует несколько способов определения знака изгибающего момента в поперечном сечении. 1. По знаку кривизны изогнутого бруса (рис. 2.19, а). Очевидно, знак будет зависеть от выбранной системы координат. Если ось у направить в противоположную сторону, то знаки М изг изменятся на противоположные.
2. Чаще всего при построении эпюр изгибающих моментов знак момента не зависит от выбранной системы отсчета, а ордината откладывается на сжатом волокне, т. е. в сторону вогнутости изогнутой оси бруса (рис. 2.19, б). 3. Если трудно представить, как будет выглядеть изогнутая ось бруса, то составляют сумму моментов нагрузок, действующих на левую отсеченную часть бруса. Если равнодействующий момент всех нагрузок, действующих на левую часть, будет направлен по часовой стрелке, то ордината изгибающего момента откладывается на эпюре вверх (т. е. изгибающий момент М изг в поперечном сечении действует против часовой стрелки и, следовательно, брус изгибается вогнутостью вверх — ордината будет отложена на сжатом волокне). Если же сумма моментов, действующих слева от сечения, направлена против часовой стрелки, то изгибающий момент на эпюре откладывается вниз (рис. 2.19, б). Для сил, лежащих справа от сечения, имеет место обратная зависимость. Правило определения знака для поперечных сил: если равнодействующая внешних сил, лежащих по левую сторону от сечения, направлена вверх, то поперечная сила в сечении считается положительной, а если вниз, то поперечная сила отрицательна. В сечении на расстоянии z 1 от начала координат, т. е. в левой части бруса от сечения (см. рис. 2.18, в), поперечная сила Q имеет положительный знак и на эпюре будет откладываться вверх. При рассмотрении равновесия правой отсеченной части для сил, лежащих справа от сечения, имеет место обратная зависимость. Чтобы легче усвоить правила определения знаков, желательно рассматривать равновесие, например, всегда левой части бруса. Дифференциальная зависимость между изгибающим моментом, поперечной силой и интенсивностью распределенной нагрузки. Правильность выбора знаков поперечных сил можно проверить, зная дифференциальную зависимость между изгибающим моментом и поперечной силой. Пусть брус, закрепленный произвольным образом, нагружен в общем случае распределенной нагрузкой интенсивности q = f (z) и находится в равновесии (рис. 2.20, а). Заданное направление для q — положительное. Выделим элемент бруса длиной dz и в сечениях приложим изгибающие моменты М и M + dM, а также поперечные силы Q и Q + dQ (рис. 2.20, б). Направления для этих силовых факторов приняты положительными в соответствии с обусловленным ранее правилом знаков. В пределах малого отрезка dz нагрузку q можно считать распределенной равномерно. Поскольку рассматриваем элемент бруса, находящегося в равновесии, то составим условия равновесия плоской системы сил: приравниваем к нулю сумму проекций всех сил на вертикальную ось и сумму моментов относительно точки С:
Откуда, отбросив величину высшего порядка малости qdz (dz /2), получим
Таким образом, поперечная сила представляет собой производную от изгибающего момента по длине бруса. Производная от поперечной силы дает интенсивность внешней распределенной нагрузки q. Из полученных дифференциальных зависимостей можно сделать некоторые общие выводы о характере эпюр изгибающих моментов и поперечных сил для прямого бруса. Если брус нагружен равномерно распределенной нагрузкой интенсивности q = const, очевидно, функция Q будет линейной, а М — квадратичной. Если брус нагружен сосредоточенными силами или моментами, а между точками их приложения интенсивность q = 0, то Q = const, a M является линейной функцией z. В точках приложения сосредоточенных сил эпюра Q претерпевает скачок на величину внешней силы, а в эпюре М возникает соответствующий излом (разрыв в производной). Построение эпюр изгибающих моментов и поперечных сил осуществляется в следующей последовательности: 1) определяют реакции опор; 2) выявляют в поперечных сечениях бруса все внутренние силовые факторы (их значение и знак); 3) строят эпюры. Построим эпюры для балки, представленной на рис. 2.18. 1. Определяем реакции опор. Составляем уравнения равновесия плоской системы сил:
2. Определяем внутренние изгибающие моменты в поперечных сечениях балки. Для этого рассматриваем равновесие отсеченной левой части (см. рис. 2.18, в): в сечении z 1
в сечении z 2
3. Определяем поперечные силы: в сечении z 1
Отсюда Q = RA = F (l - a)/ l; в сечении z 2
Отсюда Q = Fa / l. 4. Строим эпюры изгибающих моментов. Эпюра М изг в пределах 0 £ z 1 £ а имеет линейную зависимость. Задаемся z 1 = 0, при этом М изг = 0. Откладываем эту точку на эпюре (рис. 2.21). Далее при z 1 = а M изг = = F (l - a) a / l.
В пределах а £ z 2 £ l получаем: при z 2 = а M изг = F (l - a) a / l; при z 2 = l М изг = 0. Откладываем эти ординаты (они построены на сжатом волокне) и соединяем линиями. Следует заметить, что на втором участке можно было ординаты не вычислять, так как в шарнирной опоре В момент не может возникать, и поэтому на эпюре нужно сразу отложить 0. 5. Строим эпюры поперечных сил. Как было определено в п. 3, поперечные силы постоянны на каждом из двух участков, поэтому откладываем подсчитанные значения с учетом знаков. Нужно обратить внимание, что в точке приложения внешней силы должен быть скачок, равный приложенной силе. Кроме того, можно проверить правильность установленных знаков поперечных сил. Тангенс угла наклона линии М изг на эпюре изгибающих моментов показывает на знак поперечной силы. Если угол острый, то тангенс положительный (производная dM / dt > 0), а следовательно, и поперечная сила имеет знак «+». Если угол наклона линии с осью z тупой, то поперечная сила отрицательная. Сопоставьте построенные эпюры М изг и Q (см. рис. 2.21). Задача Эйлера Впервые задача об устойчивости стержня была поставлена и решена Л.Эйлером в середине XVIII в. Поэтому, когда речь идет об устойчивости сжатого стержня, употребляют выражение «устойчивость стержня по Эйлеру». Эйлер определил значение первой критической силы для продольно сжатого стержня с шарнирным опиранием (рис. 2.41).
Запишем дифференциальное уравнение изогнутой оси балки: EJy ² = - M. Изгибающий момент М = Fy (см. рис. 2.41). Подставим в правую часть дифференциального уравнения вместо изгибающего момента М его значение Fy и перенесем все члены в левую часть. В результате получим однородное дифференциальное уравнение y ² + k 2 y = 0, где k 2 = F /(EJ). Запишем решение этого однородного уравнения: y = С sin kz + D cos kz. Определим произвольные постоянные из граничных условий: при z = 0 y = 0 и при z = l y = 0. Из первого условия вытекает, что D = 0, а из второго — что С sin kl = 0. Это уравнение имеет два решения: С = 0 и sin kl = 0. Когда С = 0, перемещения y тождественно обращаются в нуль; этот случай нас не интересует. Рассмотрим второй случай. Если sin kl = 0, то kl = p n, где n = 1, 2, 3 … При n = 1 kl = p и тогда k 2 l 2 = p2. Подставив в это равенство вместо k 2 = F /(EJ), получим выражение для определения первой критической силы:
Таким образом, критическая сила F кр представляет собой наименьшую сжимающую силу, при которой наряду с прямолинейной формой равновесия становится возможной другая (изгибная) форма равновесия. Иначе говоря, прямолинейная форма равновесия становится неустойчивой. Гибкость стержня Найдем критическое напряжение
Введем в формулу радиус инерции
Тогда выражение для критического напряжения перепишем в виде
Величину m l / i обозначим через l и будем называть гибкостью стержня. При этом выражение для критического напряжения принимает вид
Основы сопротивления материалов
Основные понятия В данной главе будем рассматривать тела, которые под действием внешних сил меняют свою форму и размеры, т. е. деформируются. Деформации могут быть упругими, если тело после устранения нагрузки, т. е. внешних сил, восстанавливает свои размеры и форму. Если же после снятия нагрузки тело не восстанавливает прежней формы, то возникающие при этом деформации называются остаточными. Мы будем изучать только однородные изотропные тела, у которых по всем направлениям свойства одинаковые. В сопротивлении материалов тела классифицируют следующим образом:
В зависимости от того, какие силы приложены к брусу, он будет по-разному деформироваться. Чтобы определить напряженное состояние, применяют метод сечений. Метод сечений позволяет выявить внутренние силы и заключается в том, что тело мысленно рассекают плоскостью на две части (рис. 2.1, а) и рассматривают равновесие одной из отсеченных частей. Считают, что внутренние силы распределены равномерно, их равнодействующая равна N (рис. 2.1, б). Составим уравнение равновесия сил, действующих на отсеченную часть бруса:
Отсюда N = F.
|
|||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 362; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.15.94 (0.132 с.) |

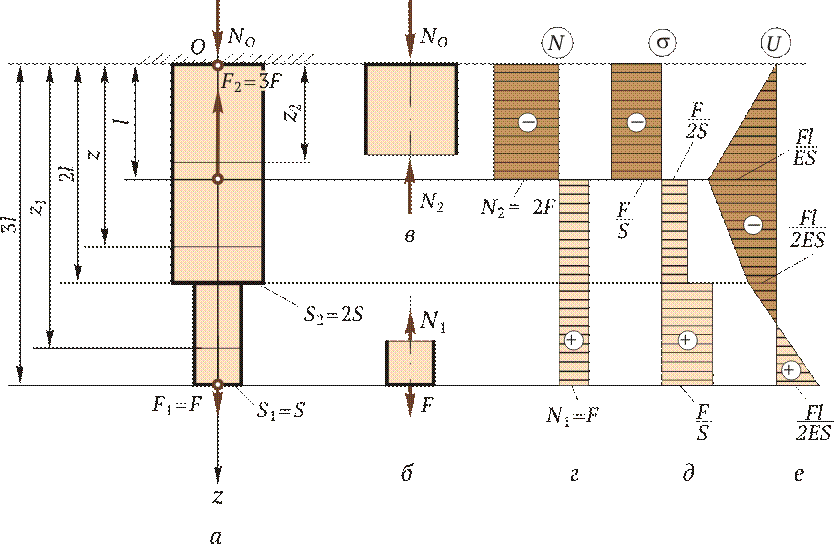 Рис. 2.3
Рис. 2.3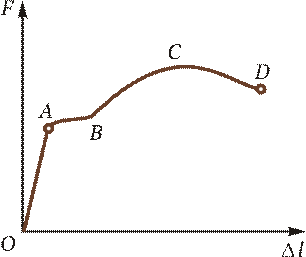 Рис. 2.4
Рис. 2.4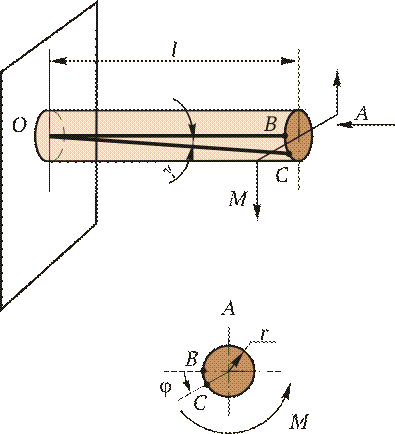 Рис. 2.9
Рис. 2.9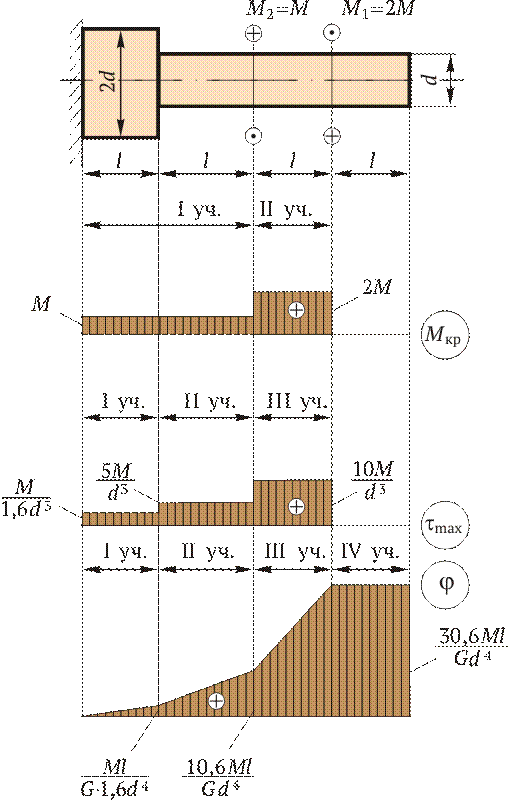 Рис. 2.10
Рис. 2.10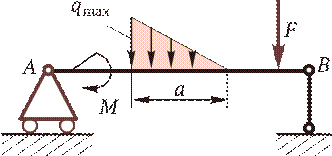 Рис. 2.17
Рис. 2.17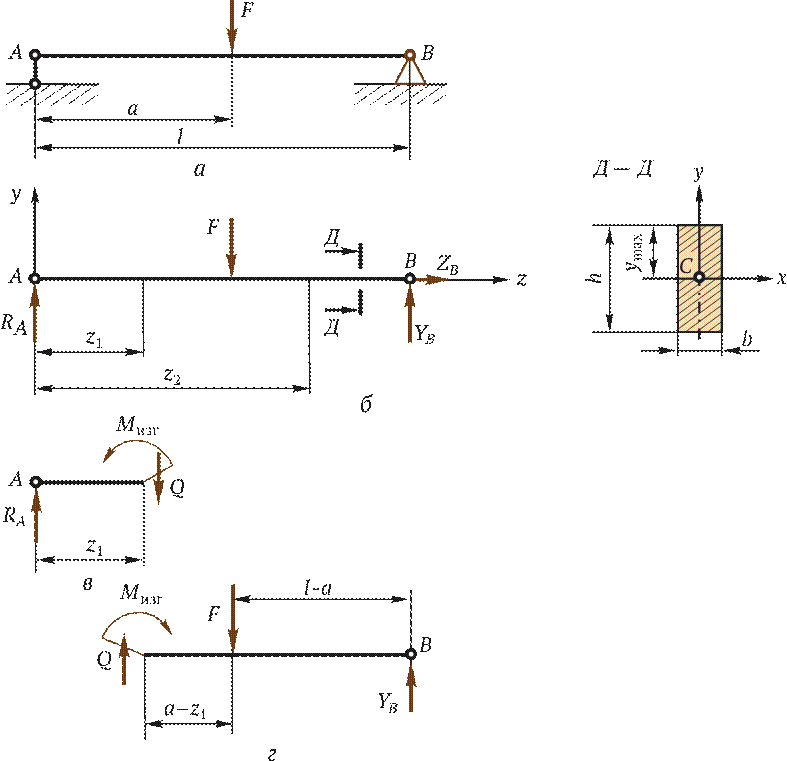 Рис. 2.18
Рис. 2.18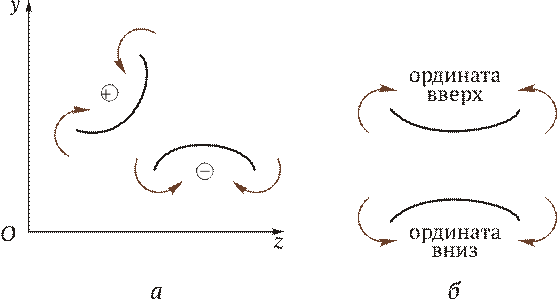 Рис. 2.19
Рис. 2.19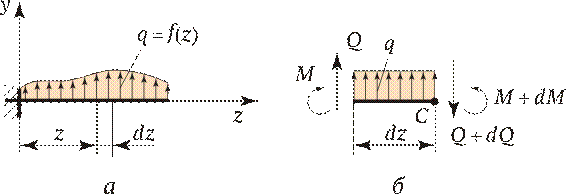 Рис. 2.20
Рис. 2.20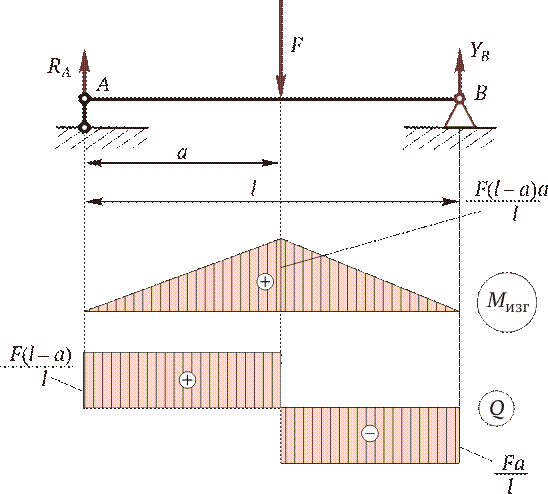 Рис. 2.21
Рис. 2.21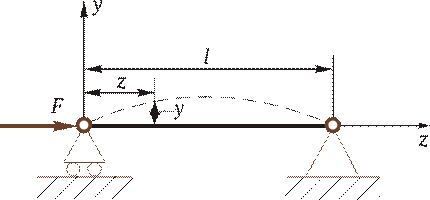 Рис. 2.41
Рис. 2.41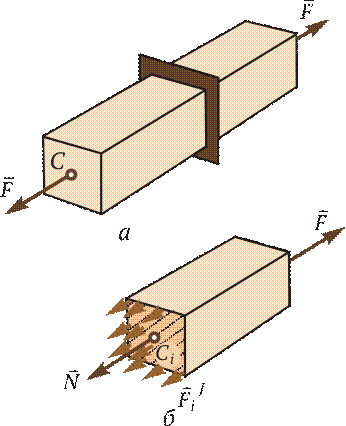 Рис. 2.1
Рис. 2.1


