
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напряжения и деформации при сдвиге (срезе)Содержание книги
Поиск на нашем сайте
В подразд. 2.1 уже упоминалось, что в поперечном сечении могут возникать как нормальные s, так и касательные напряжения t. Если к короткому брусу, жестко заделанному одним концом в стену (рис. 2.7, а), перпендикулярно оси бруса приложить силу F, то в поперечных сечениях возникнет внутренняя поперечная сила Q в плоскости сечения, а следовательно, и касательное напряжение t = Q / S.
Параллельные сечения бруса сдвигаются относительно друг друга (рис. 2.7, б) так, что верхняя грань образует угол g с горизонталью. Установлено, что касательное напряжение t прямо пропорционально угловой деформации g: t = G g, где G — модуль упругости при сдвиге. Эта зависимость выражает закон Гука для сдвига. Явление среза можно наблюдать, если стальную полосу или бумагу перерезать ножницами, или, например, в случае, когда к клепаному соединению приложена сила, бо́льшая, чем та, на которую данное соединение было рассчитано. На рис. 2.8 показано, что приложенные силы F вызывают деформацию сдвига, и под их действием может произойти срез заклепки. Вот почему сдвиг часто называют срезом.
Модуль упругости при сдвиге зависит от модуля упругости I рода Е:
Если известны Е и m, то можно определить модуль упругости при сдвиге. Например, для стали 30 Е = 2·105 Н/мм2, m = 0,3, следовательно,
Подчеркнем, что сдвиг — это напряженное состояние. Если возникшие при сдвиге деформации находятся в пределах упругости, то после снятия нагрузки размеры и форма детали восстанавливаются. Если же предел упругости превышен, то наблюдаются пластические деформации и после снятия нагрузки остается наметившееся место среза. По достижении предельных напряжений произойдет срез. Пример 2.3 Проверить прочность заклепок (см. рис. 2.8), если [t]ср = 100 Н/мм2. Решение. 1. Определяем фактическое касательное напряжение, возникающее в поперечных сечениях заклепок под действием заданных сил. Поскольку число заклепок i = 2 и они срезаются по одной плоскости (число плоскостей среза k = 1), то
2. Проверяем прочность заклепок: фактическое касательное напряжение в поперечном сечении заклепки должно быть меньше или равно допускаемому касательному напряжению на срез. Действительно, 79,6 < 100. Следовательно, под действием силы F = 50 кН не произойдет среза заклепок. Смятие При сжатии двух тел возникает опасность смятия контактирующих поверхностей. Напряжения, возникающие на контактирующих поверхностях, называются напряжениями смятия. Смятие имеет место, например, в клепаных и болтовых соединениях. Напряжение смятия определяют по формуле
где F — сила, с которой сдавливаются контактирующие поверхности; S см — площадь смятия. Если поверхность смятия является криволинейной, то площадь смятия вычисляется как площадь проекции этой поверхности на плоскость, перпендикулярную к линии действия сминающей силы. Пример 2.4 Проверить прочность клепаного соединения (см. рис. 2.8), если [t]ср = = 100 Н/мм2; [s]см = 240 Н/мм2; [s]р = 140 Н/мм2. Решение. 1. Проверяем прочность заклепки на срез (методика расчета приведена в примере 2.3). 2. Проверяем на смятие стенки отверстий в соединяемых листах:
Полученное значение фактического напряжения смятия меньше допускаемого, так как по условию [s]см = 240 Н/мм2. Следовательно, смятия стенок отверстий не произойдет. 3. Проверяем прочность листов на растяжение по формуле
Для определения опасного сечения в сложных случаях обычно строят эпюры N, а затем s. В данном случае задача более простая. Ясно, что опасным сечением является сечение А — А. Площадь поперечного сечения каждого листа S = 10·(120 - 2·20) = 800 мм2, а фактическое напряжение
что меньше допускаемого: 62,5 < 140. Ответ. Можно считать, что прочность клепаного соединения достаточна.
Кручение
Под кручением понимается такой вид нагружения, при котором в поперечных сечениях возникает только крутящий момент. Прочие внутренние силовые факторы (нормальная и поперечные силы, изгибающие моменты) равны нулю. Рассмотрим кручение круглого бруса (рис. 2.9). К круглому брусу, жестко заделанному в стенку, на свободном торце приложен крутящий момент М. В результате этого брус деформируется: смежные сечения поворачиваются относительно друг друга, образующая ОВ искривляется и занимает положение ОС.
При рассмотрении кручения принимаются следующие допущения и правила:
При кручении в поперечном сечении бруса возникают касательные напряжения (чистый сдвиг). Угол закручивания j и относительный угол закручивания θ связывает следующая зависимость: q = j/ l. Касательные напряжения t при кручении распределяются в сечении по линейной зависимости: в центре они равны нулю, а на максимальном радиусе поперечного сечения — максимальному значению tmax, по которому ведется расчет. Значение касательного напряжения зависит от внутреннего крутящего момента и геометрической характеристики поперечного сечения: tmax = M кр/ Wр, где Wp — полярный момент сопротивления. Для сплошного поперечного сечения диаметром D Wp = 0,2 D 3; для кольцевого сечения (полый вал) Wp = 0,2 D 3(1 - d 4/ D 4), где d — внутренний диаметр (диаметр отверстия); D — внешний диаметр вала. Покажем, что валы сплошного поперечного сечения использовать неэкономично. Пример 2.5 Вал передает момент M = 10000 Н·м. Требуется подобрать размеры поперечного сечения вала для случаев: а) сплошного кругового сечения и б) кругового сечения с отверстием d = (7/8) D. Сравнить оба сечения по расходу металла. Допускаемое напряжение [t] = 6000 Н/см2. Решение. 1. Определяем требуемый момент сопротивления для обоих поперечных сечений:
2. Определяем диаметр вала сплошного сечения:
3. Определяем диаметр вала полого поперечного сечения:
4. Определяем расход металла. Для этого вычислим площади поперечных сечений сплошного и полого валов: для сплошного вала
для полого вала
Поскольку расход металла будет пропорционален площади поперечного сечения, то полое сечение является более экономичным и в данном случае дает более чем двукратное снижение веса вала. Построение эпюр При кручении, как и при растяжении, строят эпюры внутренних силовых факторов (крутящих моментов), напряжений (tmax) и перемещений (углов закручивания j).
Построение эпюры М кр. Всю длину бруса (рис. 2.10) разобьем на два участка. На эпюре внутренних силовых факторов в сечениях, где приложены внешние силы, будут скачки, равные приложенным нагрузкам (в данном случае — внешним скручивающим моментам). Применяя метод сечений с учетом правила знаков для крутящих моментов, строим эпюры М кр. На рис. 2.10 для изображения внешних моментов применено условное обозначение в виде кружков: кружок с точкой обозначает силу, направленную «на себя», а кружок с крестиком — силу, направленную «от себя».
Построение эпюры tmax. Всю длину бруса разбиваем на три участка; на каждом из них М кр и Wр сохраняют постоянное значение. Затем подставляем в формулу tmax = = М кр/ Wр соответствующие значения М кр и Wр: на I участке на II участке на III участке Поскольку все внутренние крутящие моменты положительны, то и все касательные напряжения на эпюре tmax будут также положительны. Построение эпюры j. Прежде всего необходимо установить зависимость, по которой будем определять углы закручивания j. На основании закона Гука для сдвига запишем выражение для максимального касательного напряжения в поперечном сечении круглого бруса: tmax = G g. Из рис. 2.9 видно, что при кручении образующая цилиндра ОВ поворачивается на угол g и занимает положение ОС. При этом дуга ВС равна g l; с другой стороны, та же дуга ВС равна j r. Следовательно, g l = j r, откуда g = j r / l. Подставляя найденное значение g в закон Гука, получим
С другой стороны, t = M кр/ Wр. Следовательно,
Выразим отсюда угол закручивания Величину Wpr (или WpD /2) называют полярным моментом инерции сечения и обозначают Jp. Таким образом, между моментом сопротивления и полярным моментом инерции бруса круглого поперечного сечения диаметром D существует следующая зависимость:
Полярный момент инерции: для сплошного круглого бруса Jp @ 0,1 D 4; для полого круглого бруса
Запишем выражение для угла закручивания j в виде
Произведение GJp называют жесткостью бруса при кручении. Итак, получена зависимость, по которой можно определять углы закручивания бруса. Определять угол закручивания по этой зависимости можно только при условии, что на длине l все входящие в эту формулу величины М кр, Jp и G — постоянные.
Переходим к построению эпюры угловых перемещений. Вал по длине разбиваем на четыре участка. Так же, как и при построении эпюры перемещений при растяжении, начинаем строить эпюру от неподвижного сечения, т. е. от жесткой заделки. В конце I участка угол закручивания
В конце II участка угол закручивания
В конце III участка
На IV участке угол закручивания будет равен углу закручивания jIII, так как на этом участке отсутствуют внутренние крутящие моменты. Вычисленные угловые перемещения откладываем на эпюре j.
Прямой поперечный изгиб
|
||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 530; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.156.35 (0.012 с.) |

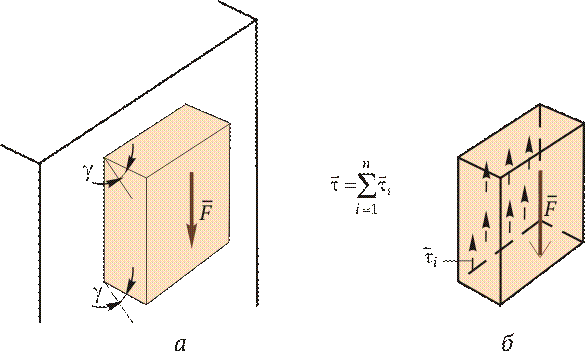 Рис. 2.7
Рис. 2.7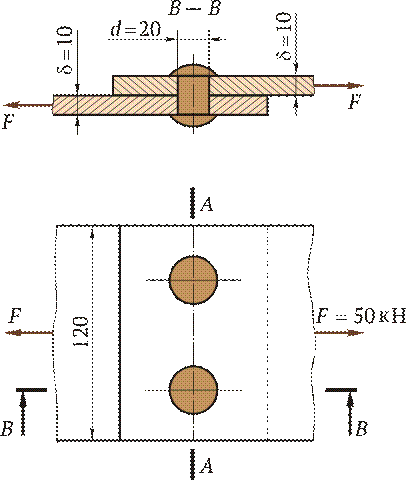 Рис. 2.8
Рис. 2.8
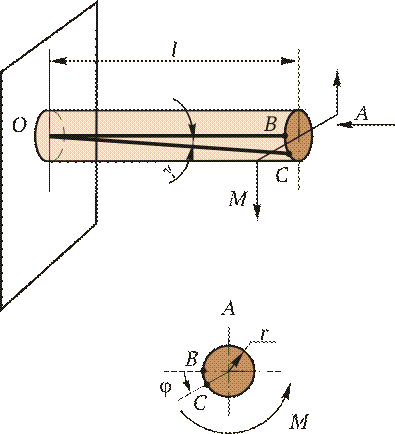 Рис. 2.9
Рис. 2.9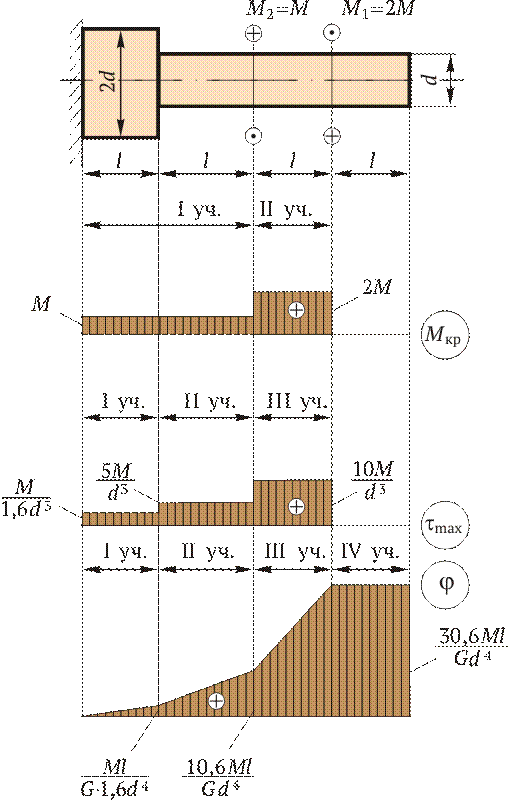 Рис. 2.10
Рис. 2.10


