
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Бинарные отношения. Прямое произведение множествСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Бинарным отношением r называется множество упорядоченных пар. Если r есть некоторое отношение и пара (х, у) принадлежит этому отношению, то употребляется запись (х, у)Î r или х rу. Элементы х и у называются координатами или компонентами (объектами) отношения r. Если х и у компоненты (объекты), то через (х, у) обозначают упорядоченную пару. Равенство упорядоченных пар определяется следующим образом: (а, b) = (с, d):= а = с и b = d (:= – операция присваивания). Областью определения бинарного отношения r называется множество D r = { x ׀существует такое у, что х rу }. Областью значений бинарного отношения r называется множество R r = { y ׀существует такое x, что х rу }. Так как бинарное отношение – множество, то способы задания бинарного отношения такие же, как и способы задания множества. Бинарное отношение может быть задано перечислением упорядоченных пар или указанием общего свойства упорядоченных пар. Кроме того, бинарное отношение может быть задано матрицей бинарного отношения. Пусть А = { a 1, a 2, …, a n } – конечное множество. Матрица бинарного отношения C есть квадратная матрица порядка n, элементы которой cij определяются следующим образом: cij = Пример. А = {1, 2, 3, 4}. Зададим бинарное отношение r тремя перечисленными способами. 1. r = {(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)} – отношение задано перечислением всех упорядоченных пар. 2. r = {(ai, aj) ç ai < aj; ai, aj Î А } – отношение задано указанием свойства "меньше" на множестве А. 3. Пусть даны два множества Х и У. Прямым (декартовым) произведением двух множеств Х и У называется совокупность всех упорядоченных пар (х, у), таких, что х Î Х и у Î У. Обозначается прямое произведение множеств Х и У через Х × У: Х × У:= {(х, у)| х Î Х и у Î У }. Каждое отношение r есть подмножество прямого произведения некоторых множеств Х и У, таких, что D r Í Х и R r Í У, то есть r Ì Х ´ У. Если Х = У, то говорят, что r есть отношение на множестве Х, и тогда r Ì Х 2. Примеры. 1. Пусть Х = {1, 2, 3}, У = {0, 1}. Тогда Х ´ У = {(1, 0), (1, 1), (2, 0), (2, 1), (3, 0), (3, 1)}; У ´ Х = {(0, 1), (0, 2), (0, 3), (1, 1), (1, 2), (1, 3)}. Пусть r есть отношение на множестве Х. Введем понятия: обратное отношение: r -1 = {(х, у)| (у, х) Î r }; дополнение отношения: ` r = {(х, у)| (х, у)Ï r }; тождественное отношение: I = {(х, x)| х Î x }. Композицией отношений r 1 и r 2 называется отношение r1О r 2 = {(х, z)| существует у такое, что (х, у) Î r 1 и (у, z)Î r 2}. Для любых бинарных отношений выполняются следующие свойства: 1) (r -1)-1 = r; 2) r2О r 1 = r 1 - 1 О r 2 -1. Пример. r = {< x, y > çy = s Свойства отношений Отношение r называется рефлексивным на множестве X, если для любого x Î X выполняется x r x. Из определения следует, что всякий элемент (x, x) Î r. Пример. 1. Пусть X – конечное множество, X = {1, 2, 3} и r = {<1, 1>, <1, 2>, <2, 2>, <3, 1>, <3, 3>}. Отношение r рефлексивно. Если X – конечное множество, то главная диагональ матрицы рефлексивного отношения содержит только единицы. Для данного примера 2. Пусть X – множество действительных чисел и r – отношение равенства. Это отношение рефлексивно, т. к. каждое число равно самому себе. Отношение r называется симметричным на множестве X, если для любых x, y Î X из x r y следует y r x. Очевидно, что r симметрично тогда и только тогда, когда r = r – 1. Пример. 1. Пусть X – конечное множество, X = {1, 2, 3} и r = {<1, 1>, <1, 2>, <1, 3>, <2, 1>, <2, 2>, <3, 1>, <3, 3>}. Отношение r симметрично. Если X – конечное множество, то матрица симметричного отношения симметрична относительно главной диагонали. Тогда 2. Пусть X – множество действительных чисел и r – отношение равенства. Это отношение симметрично, т. к. если x равно y, то и y равно x. Отношение r называется транзитивным на множестве X, если для любых x, y, z Î X из x r y и y r z следует x r z. Одновременное выполнение условий x r y, y r z, x r z означает, что пара < x, z > принадлежит композиции r Пример. Пусть X – конечное множество, X = {1, 2, 3} и r = {<1, 1>, <1, 2>, <2, 3>, <1, 3>}. Отношение r транзитивно, т. к. наряду с парами < x, y >и < y, z >имеется пара< x, z >. Например, наряду с парами <1, 2> и <2, 3> имеется пара <1, 3>. Задания Для аудиторных занятий 1. Перечислить элементы множеств А ´ В, В ´ А:
2. Пусть А, В Í С. Доказать, что А ´ В = (А ´ С) Ç (С ´ В). 3. Пусть А, В, С, D – непустые множества. Доказать следующие тождества:
4. Доказать, что для любых непустых множеств А, В, С из равенства (А ´ В) È (В ´ А) = С ´ С следует, что А = В = С. 5. Перечислить все элементы бинарного отношения r:
6. Для каждого из следующих бинарных отношений, определенных на множестве R, найти область определения, область значений и нарисовать декартову диаграмму, то есть изобразить на плоскости множество всех точек (х, у), таких, что х rу:
7. Для бинарного отношения r между элементами множеств А и В найти область определения D r и область значений R r: А = {1, 2, 3, 4, 5}, В = {{1}, {1, 2}, 3, 4, 5}. 8. Найти r -1, rО r, r - 1 О r, rО r- 1 отношений:
9. Задано бинарное отношение r = {<1, 1>, <3, 4>, <1, 4>, <4, 1>, <4, 3>}. Найти D (r), R (r), r 10. Привести пример отношения нетранзитивного, нерефлексивного и несимметричного. Для самостоятельной работы 1. Перечислить элементы множеств А ´ В, В ´ А:
2. Пусть А = { и, л }. Перечислить элементы множеств А 2, А 3. 3. Определить упорядоченную пару á a, b ñ как множество {{ a }, { a, b }}. Доказать, что á a, b ñ = á c, d ñ тогда и только тогда, когда a = c и b = d. 4. Пусть на плоскости задана декартова система координат. Изобразить на плоскости следующие множества: а) [ a, b ] ´ [ c, d ], где a, b, c, d Î R и a < b, c < d; б) [ a, b ]2. 5. Доказать, что подмножество С множества А ´ В является прямым произведением некоторого подмножества А 1 множества А и подмножества В 1 множества В тогда и только тогда, когда для любых пар á a, b ñ, á c, d ñ из С пары á a, b ñ, á c, d ñ также принадлежат С. 6. Перечислить все элементы бинарного отношения r и нарисовать его график:
7. Для каждого из следующих бинарных отношений, определенных на множестве R, найти область определения, область значений:
8. Какими свойствами обладают следующие бинарные отношения (рефлексивность, симметричность, транзитивность), заданные на R?
9. Привести пример отношения транзитивного, рефлексивного и симметричного. 10. Для каждого из следующих бинарных отношений выяснить, какими свойствами (рефлексивность, симметричность, антисимметричность, транзитивность) оно обладает. Дать обоснование ответа.
Литература 1. Куликов, Л. Я. Сборник задач по алгебре и теории чисел / Л. Я. Куликов, А. И. Москаленко, А. А Фомин. – М.: Просвещение, 1993. – 288 с. 2. Иванов, Б. Н. Дискретная математика. Алгоритмы и программы: учеб. пособие для вузов / Б. Н. Иванов. – М.: Лаборатория базовых знаний, 2002. – 288 с. 3. Новиков, Ф. А. Дискретная математика для программистов: учебник для вузов / Ф. А. Новиков. – СПб.: Питер, 2005. – 304 с.
Практическое занятие № 3
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 713; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||

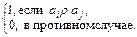
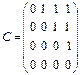 – отношение задано матрицей отношения C.
– отношение задано матрицей отношения C.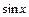 }. s = {< x, y > ç y =
}. s = {< x, y > ç y = 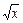 }.
}.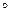 r = {< x, z > çсуществует такое y, что < x, y > Î r и < y, z > Î s } = {< x, z > çсуществует такое y, что y =
r = {< x, z > çсуществует такое y, что < x, y > Î r и < y, z > Î s } = {< x, z > çсуществует такое y, что y = 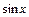 и z =
и z = 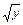 } = {< x, z > ç z =
} = {< x, z > ç z = 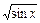 }.
}.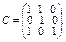
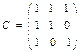 .
.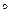 r. Поэтому для транзитивности r необходимо и достаточно, чтобы множество r
r. Поэтому для транзитивности r необходимо и достаточно, чтобы множество r 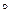 r являлось подмножеством r, т. е. r
r являлось подмножеством r, т. е. r 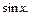
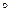 r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?


