
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формулы логики булевых функцийСодержание книги
Поиск на нашем сайте
Формула логики булевых функций определяется индуктивно следующим образом: 1. Любая переменная, а также константы 0 и 1 есть формула. 2. Если A и B – формулы, то A, A Ú B, A & B, A 3. Ничто, кроме указанного в пунктах 1–2, не есть формула. Пример. Построим таблицу значений функции f (x 1, x 2, x 3) = Ø(x 2 Таблица 3
Формула так же, как и таблица, может служить способом задания функции. Этот способ аналогичен аналитическому способу задания функций действительной переменной. При этом применяются следующие соглашения: а) вначале выполняются операции в скобках (внешние скобки у формул опускаются); б) считается, что связка Ø сильнее любой двухместной связки; в) связка & сильнее любой другой двухместной связки. Кроме того, имея в виду стандартное расположение наборов, булеву функцию f( Фиктивные и существенные переменные Фиктивные переменные. Переменная x i (1 £ i £ n) функции f(x 1, …, xn) называется фиктивной переменной, если значение функции не зависит от значения этой переменной, т. е. для любых значений переменных x1, …, x i-1, x i+1,..., x n f(x 1, …, x i-1, 0, x i+1, …, x n) = f(x 1, …, x i-1, 1, x i+1, …, x n). Переменная x i (1£ i £ n) функции f(x 1, …, x n) называется существенной переменной, если можно указать наборы Булевы функции f и g называются равными, если их существенные переменные соответственно равны и на каждом наборе значений этих переменных функции f и g принимают равные значения. Замечание: при решении практических задач иногда вместо удаления фиктивных переменных в одной из функций, наоборот, добавляют фиктивные переменные к множеству переменных другой функции.
Пример. Функции f1 = x Å y, f2 = x y Å z, f3 = x Å y Å z Å 1, f4 = xy Å yz Å zx, реализованные формулами, задать векторами своих значений. Решение. 1. Составим вначале таблицу истинности для f1, f2, f3, f4 (табл. 4). Таблица 4
2. Тогда функции f1, f2, f3, f4 задаются следующими векторами своих значений: f1( f3( 3. f2 ¹ f4, т. к. (0, 1, 0, 1, 0, 1, 1, 0) ¹ (0, 0, 0, 1, 0, 1, 1, 1) (в таблице не совпадают значения в столбцах, соответствующих этим функциям). 4. Выписываем f(0, 0, 0) = f(0, 1, 1) = f(1, 0, 1) = f(1, 1, 0) = 1 и f(0, 0, 1) = f(0, 1, 0) = f(1, 0, 0) = f(1, 1, 1) = 0. Определим, какой переменной является x. Сравнивая значения функции на всех парах наборов, соседних по переменной x, видим, что f(0, y, z)¹ f(1, y, z), x – существенная переменная. Аналогично устанавливаем, что у и z являются существенными переменными.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 102; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.26.174 (0.009 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

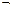 B, A ~ B есть формулы.
B, A ~ B есть формулы.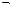 Ø x 3) ~ (Ø x 1Ú x 2). Табл. 3 представляет последовательное вычисление этой функции.
Ø x 3) ~ (Ø x 1Ú x 2). Табл. 3 представляет последовательное вычисление этой функции.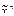 ) удобно задавать вектором ее значений:
) удобно задавать вектором ее значений:  f = (α0, α1, …,
f = (α0, α1, …, 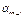 ), где координата α i равна значению функции f(
), где координата α i равна значению функции f(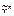 ) на наборе
) на наборе 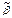 , имеющем номер i (i = 0, 1, …, 2 n – 1).
, имеющем номер i (i = 0, 1, …, 2 n – 1).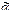 и
и 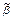 , соседние по i -ой компоненте, что f(
, соседние по i -ой компоненте, что f(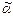 ) ¹ f(
) ¹ f(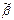 ), т. е. f(a 1, …, a i-1, 0, a i+1, …, a n) ¹ f(a 1, …, a i-1, 1, a i+1, …, a n).
), т. е. f(a 1, …, a i-1, 0, a i+1, …, a n) ¹ f(a 1, …, a i-1, 1, a i+1, …, a n).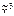 ) = (0, 0, 1, 1, 1, 1, 0, 0); f2(
) = (0, 0, 1, 1, 1, 1, 0, 0); f2(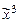 ) = (0, 1, 0, 1, 0, 1, 1, 0);
) = (0, 1, 0, 1, 0, 1, 1, 0);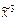 ) = (1, 0, 0, 1, 0, 1, 1, 0); f4(
) = (1, 0, 0, 1, 0, 1, 1, 0); f4(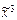 ) = (0, 0, 0, 1, 0, 1, 1, 1).
) = (0, 0, 0, 1, 0, 1, 1, 1).


