
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение диаграмм Эйлера-Венна при решении практических задачСодержание книги
Поиск на нашем сайте
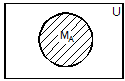
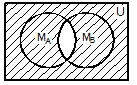
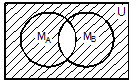
Для наглядного представления множеств и отношений между ними используются диаграммы Эйлера-Венна. Универсальное множество изображают в виде прямоугольника, а множества, входящие в универсальное множество, в виде кругов внутри прямоугольника; элементу множества соответствует точка внутри круга (рис. 1). С помощью диаграмм Эйлера-Венна удобно иллюстрировать операции над множествами. Результирующее множество каждой операции выделено штриховкой.
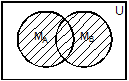
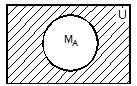
Рис. 1. Представление операций над множествами с помощью диаграмм Эйлера-Венна Пример. Рассмотрим операцию дополнения множества, являющегося пересечением множеств MА и MВ. Необходимо доказать, что её результат совпадает с объединением дополнений этих множеств: Решение. M = В этом можно убедиться с помощью диаграмм Эйлера-Венна (рис. 2).
Рис. 2 Для любых подмножеств А, В и С универсального множества U выполняются следующие тождества (основные тождества алгебры множеств):
Примеры. 1. Рассмотрим предположение о том, что произвольные множества A и B попарно эквивалентны: 1) A Ì B; 2) A Ç B = A; 3) A È B = B. Решение. Докажем, что из первого предположения следует второе. Действительно, так как A Ç B Ì A, то достаточно показать, что в этом случае A Ì A Ç B. Но если х Î A, то х Î B, т. к. A Ì B и, следовательно, х Î A Ç B. Докажем, что из второго предположения следует третье. Так как A Ç B = A, то A È B = (A Ç B) È B. По закону поглощения (см. тождество 9) B È (A Ç B) = B. Отсюда, используя закон коммутативности, получаем A È B = B. Докажем, что из третьего предположения следует первое. Так как A Ì A È B, а по условию третьего предположения A È B = B, то А Ì В. Задания Для аудиторных занятий 1.Записать множество М целых чисел х, которые делятся на три и находятся в интервале 3 £ х £ 15. Записать двумя способами. 2.Записать множество А целых чисел х, которые делятся на 2 и на 3 и находятся в интервале 20 £ х £ 25. Записать двумя способами. 3.Принадлежит ли х множеству М, если: а) М = {2, 6, 8, …, 50}; х = 35; б) М = {2, 3, 4, 6, 8, 9, 10, …, 100}; х = 23; в) М = {-2, 2, -4, 4, …, 120}; х = -30. Записать приведенные множества с указанием свойств их элементов. 4.Доказать неравенство: {{1, 2}, { 2, 3}} ¹ {1, 2, 3}. 5.Какие из следующих выражений являются истинными и какие ложными: а) Æ Î {{Æ}}; б) 1 Î {{1, 2}}; в) {1, 2} Î {{1, 2}}; г) {1, 2} Î {{1, 2}, {1, 3}, 1, 2}. 6. Привести примеры таких множеств А, В, С, чтобы были истинными следующие высказывания: а) А Î В Ù В Î С Ù А Ï С; б) А Î В Ù В Î С Ù А Î С. 7. Какие из следующих множеств конечны и какие бесконечны: а) { x Î R ç x 2 - 5 x + 4 = 0}; б) { x Î N ç x 2 - 5 x + 4 > 0}; в) { x Î N ç x 2 / 24}. 8. Равны ли множества: а) { x Î R ç x 2 - 2 x – 2 = 0} и { x Î Q ç x 2 - 2 x – 2 = 0}; б) { x Î Z ç4/ x Ù 15/ x } и { x Î Z ç4/ x Ù 15/ x }{ x Î Z ç20/ x Ù 30/ x }. 9. Перечислить элементы следующих множеств: а) { x Î R ç x 2 - 3 x + 2 = 0}; б) { x Î R ç x 2 + 1 = 0}; в) множество всех корней уравнения x 2 + 6 x + 9 = 0. 10. Перечислить все элементы каждого из следующих множеств: а) { x ç x Í{ 1}}; в) { x ç x Í {1, 2, 3}}; б) { x ç x Í {1, 2}}; г) { x ç x Í Æ}. Для самостоятельной работы 1. Перечислить элементы следующих множеств: а) множество четных чисел от 0 до 20 включительно; б) множество всех двузначных чисел, делящихся на 5 и не делящихся на 10; в) множество всех последовательностей, содержащих все числа 1, 2, 3, 4, 5 и только эти числа, в которых четные и нечетные числа чередуются. 2. Равны ли множества: а) {2, 4, 5} и {2, 4, 2, 5}; б) {1, 2} и {{1, 2}}; в) {1, 2, 3} и {3, 1, 2, 1}}; г) {1, 2, 3} и {{1}, {2},{3}}. 3. Перечислить подмножества следующих множеств: а) {{1, 2}, {3}, 4}; б) {{5, 2}}; в) {{2}, {6}, {3} }; г) {{4, 6}, {1}, 1}. 4. Вставить между множествами символ Î или Ì так, чтобы получилось истинное высказывание: а) {1} {1, {1, 2}}; б) Æ {Æ}; в) Æ {{Æ}}; г) {1, 2} {1, 2, {1, 2}}. 5. Найти А È В, А Ç В, А \ В, В \ А,` А,` В: а) А = {1, 2, 3}, В = {2, 3, 5, 4}, U = {1, 2, …, 9}; б) А = { х ׀ х делится на 2}, В = { х ׀ х делится на 3}, U = N. 6. Доказать следующие тождества:
7. Показать с помощью диаграмм Эйлера-Венна, какие из следующих утверждений верны:
8. Найти мощность множеств, мощность их булеанов и | А È В | – мощность объединения множеств: а) А = {4, 5, 6}, В = {4, 5, 6, 7, 8}; б) А = {1, 3, 5, 6}, В = {4, 5, 6, 7}; в) А = {3, 5, 7}, В = {2, 5, 6, 7, 9}; г) А = {1, 2, 3, 5}, В = {2, 4, 5, 6, 7}. 9. Вставить между множествами символ Î или Í так, чтобы получилось истинное высказывание: а) {1} {1, {1, 2}}; г) Æ {1, 2, {1}, {Æ}}; б) {1, 2} {1, 2, {1},{2}}; д) Æ {{Æ}}; в) {1, 2} {1, 2,{1, 2}}; е) Æ {Æ}. 10. Привести пример множеств A, B, C, таких, чтобы выполнялись условия: а) A Î B, B Ï C, A Í C; б) A Î B, A Ï C, C Í B; в) A Í B, B Î C, A Ï C. Литература 1. Куликов, Л. Я. Сборник задач по алгебре и теории чисел / Л. Я. Куликов, А. И. Москаленко, А. А Фомин. – М.: Просвещение, 1993. – 288 с. 2. Ерусалимский, Я. М. Дискретная математика. Теория, задачи, приложения: учеб. пособие для вузов / Я. М. Ерусалимский. – М.: Вузовская книга, 2008. – 288 с. 3. Новиков, Ф. А. Дискретная математика для программистов: учебник для вузов / Ф. А. Новиков. – СПб.: Питер, 2001. – 304 с.
Практическое занятие № 2 Тема: «Бинарные отношения» Цель занятия: усвоение таких понятий, как упорядоченная пара, прямое произведение множеств, бинарное отношение, типы бинарных отношений, свойства (рефлексивность, антирефлексивность, симметричность, антисимметричность, транзитивность). Пояснение к работе Время выполнения практического задания – 2 часа. Последовательность выполнения 1. Руководствуясь приведенным теоретическим материалом, ответить на следующие вопросы: Какие способы задания бинарного отношения вы знаете? Что является областью определения бинарного отношения r? Что является областью значений бинарного отношения r? Какое отношение r называется рефлексивным на множестве X? Какое отношение r называется симметричным на множестве X? Главная диагональ матрицы какого отношения содержит только единицы? Для какого отношения r всегда выполняется условие r = r – 1? Для какого отношения r всегда выполняется условие r 2. Дать определение следующих понятий: – бинарное отношение; – композиция отношений. 3. Выполнить задания для аудиторных занятий. 4. Выполнить задания для самостоятельной работы.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 270; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.01 с.) |

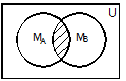
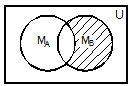
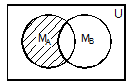
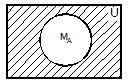
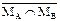 =` MА È` MВ.
=` MА È` MВ.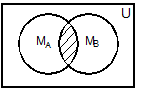
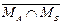
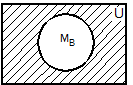
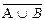 =` А Ç` В (закон де Моргана).
=` А Ç` В (закон де Моргана).
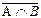 =` А È` В (закон де Моргана).
=` А È` В (закон де Моргана).
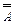 = А (инволюция).
= А (инволюция).
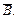
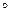 r Í r.
r Í r.


