
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Камышинский технологический институт (филиал)Содержание книги
Поиск на нашем сайте
Предисловие В настоящее время в связи с широким использованием вычислительной техники в различных сферах человеческой деятельности все большее значение приобретают вычисления на дискретных структурах. Решением задач реальной размерности с учетом ограниченности временных и емкостных ресурсов ЭВМ занимается дискретная математика. Дискретная математика – самостоятельное направление современной математики, она изучает математические модели объектов, процессов, зависимостей, существующих в реальном мире, с которыми имеют дело в вычислительной технике, программировании и других областях знаний. Дискретная математика является сердцевиной математической кибернетики и представляет собой важное направление, имеющее характерные для него предмет исследований, методы и задачи. Задачи анализа и конструирования сложных систем послужили стимулом для разработки теории графов: задачи хранения, обработки и передачи информации привели к теории кодирования (дискретной теории информации); задачи оптимизации вызвали появление дискретного программирования; исследование основных понятий вычислительной математики – вычислимости и алгоритма – стимулировало появление теории алгоритмов. В широком смысле дискретная математика включает в себя такие сложившиеся математические разделы, как теория множеств и отношений, математическая логика и ряд других, которые стали развиваться наиболее интенсивно в связи с внедрением вычислительной техники. В узком смысле она ограничивается следующими разделами: теория функциональных систем, теория графов, теория автоматов, теория кодирования, теория алгоритмов, комбинаторный анализ и др. Материал, рассматриваемый в курсе дискретной математики, формирует культуру абстрактного мышления, развивает умение проводить анализ, композицию и декомпозицию информационных комплексов и информационных процессов и предназначен для студентов, изучающих информатику и вычислительную технику.
Порядок выполнения практических заданий В полном объеме освоить теоретический материал по соответствующей теме. Четко знать определения, ориентироваться в терминах и обозначениях рассматриваемых понятий. Использовать математический аппарат дискретной математики при решении типовых задач в предметной области. Рассмотреть конкретные примеры выполнения заданий. Выполнить задания, предложенные для самостоятельной работы. Представить результат выполнения работы в письменном виде с подробным объяснением хода решения задачи и теоретическими выкладками. Качество выполнения заданий контролируется преподавателем и оценивается им в соответствии с методикой рейтингового контроля. Практическое занятие № 1 Тема: «Начальные понятия теории множеств. Операции над Множествами. Применение диаграмм Эйлера-Венна при Решении практических задач» Цель занятия: познакомить студентов с такими понятиями, как множество, элементы множеств, булеан, универсальное множество, мощность множества, операции над множествами, представления множеств с помощью диаграмм, формируя у них терминологический запас. Пояснение к работе Время выполнения практического задания – 4 часа. Последовательность выполнения 1. Руководствуясь приведенным теоретическим материалом, ответить на следующие вопросы: Как обозначаются множества и элементы множеств? Какое множество называется конечным? Какие существуют способы задания множеств? Как определяется мощность множества? 2. Дать определение следующих понятий: – множество и элементы множества; – операции разности и объединения множеств; – операции пересечения и дополнения; – универсальное множество и булеан. 3. Перечислить основные тождества алгебры множеств. 4. Представить операции над множествами в виде диаграмм. 5. Выполнить задания для аудиторных занятий. 6. Выполнить задания для самостоятельной работы. Операции над множествами Объединением А и В называется множество А È В, все элементы которого являются элементами хотя бы одного из множеств А или В: А È В = { x ç x Î А и / или x Î В }. Из определения следует, что А Í А È В и В Í А È В. Аналогично определяется объединение нескольких множеств. Пример. 1. Пусть А = {4, 5, 6}, В = {2, 4, 6}. Тогда А È В = {2, 4, 5, 6}. 2. Пусть А – множество чисел, которые делятся на 2, а В – множество чисел, которые делятся на 3: А = {2, 4, 6, …}, В = {3, 6, 9, …}. Тогда А È В – множество чисел, которые делятся на 2 или на 3: А È В = {2, 3, 4, 6, 8, 9, 10, …}. Пересечением множеств А и В называется множество А Ç В, все элементы которого являются элементами обоих множеств А и В: А Ç В = { x ç x Î А и x Î В }. Из определения следует, что А Ç В Í А, А Ç В Í В и А Ç В Í А È В. Аналогично определяется пересечение нескольких множеств. Пример. 1. Пусть А = {4, 5, 6}, В = {2, 4, 6}. Тогда А Ç В = {4, 6}. 2. Пусть А – множество чисел, которые делятся на 2, а В – множество чисел, которые делятся на 3: А = {2, 4, 6, …}, В = {3, 6, 9, …}. Тогда А Ç В – множество чисел, которые делятся и на 2, и на 3: А È В = {6, 12, 18, …}. Может оказаться, что множества не имеют ни одного общего элемента. Тогда говорят, что множества не пересекаются или что их пересечение – пустое множество. Пример. Пусть А = {1, 2}, В = {2, 3}, C = {3, 4}. Тогда А Ç В Ç C = Æ. Разностью (относительным дополнением) множества В до множества А называется множество А \ В, все элементы которого являются элементами множества А, но не являются элементами множества В: А \ В = { x ç x Î А и x Ï В }. Пример. 1. А = {4, 5, 6}, В = {2, 4, 6}. А \ В = {5}, В \ А = {2}. 2. А = {2, 4, 6, …}, В = {3, 6, 9, …}. Тогда А \ В – множество чисел, которые делятся на 2, но не делятся на 3, а В \ А – множество чисел, которые делятся на 3, но не делятся на 2: А \ В = {2, 4, 8, 10, 14, …}. В \ А = {3, 9, 15, 21, 27, …}. Симметрической разностью множеств А и В называется множество А + В: А + В = (А \ В) È (В \ А). Пример. 1. А = {4, 5, 6}, В = {2, 4, 6}. А \ В = {5}, В \ А = {2}, А + В = {2, 5}. 2. А = {2, 4, 6, …}, В = {3, 6, 9, …}, А \ В = {2, 4, 8, 10, 14, …}. В \ А = {3, 9, 15, 21, 27, …}, А + В = {2, 3, 4, 8, 9, …}. Дополнением ` М множества М является множество ` М = { mi │ mi Ï M }. Пример. Заданы множества А = {1, 2, 5, 6} и В = {2, 3, 4, 6} на универсальном множестве U = {1, 2, 3, 5, 6, 7}. Выполнить операции` А, `В. Решение. В результате выполнения заданных операций получим следующие множества: ` А = {3, 7};` В = {1, 5, 7}. Для конечных множеств существует понятие: мощность множества А – число его элементов. Обозначают мощность множества | А |. Пример. А = {1, 2, 5, 6}, тогда мощность множества | А | = n(А) = 4; |Æ| = 0; |{Æ}| = 1. Также справедливы следующие формулы: для любых множеств А и В Þ | А È В | = | А | + | В | – | А Ç В |, то есть учитываются общие для обоих множеств элементы. Пример. А = {1, 2, 3} | А | = 3; В = {1, 2, 3, 4, 5} | В | = 5, тогда А È В = {1, 2, 3, 4, 5} | А È В | = 5; А Ç В = {1, 2, 3} | А Ç В | = 3, то есть получим равенство: | А È В | = | А | + | В | – | А Ç В | 5 = 3 + 5 – 3. Для конечного множества М мощность его булеана | В(М) | равна 2|М|. Задания Для аудиторных занятий 1.Записать множество М целых чисел х, которые делятся на три и находятся в интервале 3 £ х £ 15. Записать двумя способами. 2.Записать множество А целых чисел х, которые делятся на 2 и на 3 и находятся в интервале 20 £ х £ 25. Записать двумя способами. 3.Принадлежит ли х множеству М, если: а) М = {2, 6, 8, …, 50}; х = 35; б) М = {2, 3, 4, 6, 8, 9, 10, …, 100}; х = 23; в) М = {-2, 2, -4, 4, …, 120}; х = -30. Записать приведенные множества с указанием свойств их элементов. 4.Доказать неравенство: {{1, 2}, { 2, 3}} ¹ {1, 2, 3}. 5.Какие из следующих выражений являются истинными и какие ложными: а) Æ Î {{Æ}}; б) 1 Î {{1, 2}}; в) {1, 2} Î {{1, 2}}; г) {1, 2} Î {{1, 2}, {1, 3}, 1, 2}. 6. Привести примеры таких множеств А, В, С, чтобы были истинными следующие высказывания: а) А Î В Ù В Î С Ù А Ï С; б) А Î В Ù В Î С Ù А Î С. 7. Какие из следующих множеств конечны и какие бесконечны: а) { x Î R ç x 2 - 5 x + 4 = 0}; б) { x Î N ç x 2 - 5 x + 4 > 0}; в) { x Î N ç x 2 / 24}. 8. Равны ли множества: а) { x Î R ç x 2 - 2 x – 2 = 0} и { x Î Q ç x 2 - 2 x – 2 = 0}; б) { x Î Z ç4/ x Ù 15/ x } и { x Î Z ç4/ x Ù 15/ x }{ x Î Z ç20/ x Ù 30/ x }. 9. Перечислить элементы следующих множеств: а) { x Î R ç x 2 - 3 x + 2 = 0}; б) { x Î R ç x 2 + 1 = 0}; в) множество всех корней уравнения x 2 + 6 x + 9 = 0. 10. Перечислить все элементы каждого из следующих множеств: а) { x ç x Í{ 1}}; в) { x ç x Í {1, 2, 3}}; б) { x ç x Í {1, 2}}; г) { x ç x Í Æ}. Для самостоятельной работы 1. Перечислить элементы следующих множеств: а) множество четных чисел от 0 до 20 включительно; б) множество всех двузначных чисел, делящихся на 5 и не делящихся на 10; в) множество всех последовательностей, содержащих все числа 1, 2, 3, 4, 5 и только эти числа, в которых четные и нечетные числа чередуются. 2. Равны ли множества: а) {2, 4, 5} и {2, 4, 2, 5}; б) {1, 2} и {{1, 2}}; в) {1, 2, 3} и {3, 1, 2, 1}}; г) {1, 2, 3} и {{1}, {2},{3}}. 3. Перечислить подмножества следующих множеств: а) {{1, 2}, {3}, 4}; б) {{5, 2}}; в) {{2}, {6}, {3} }; г) {{4, 6}, {1}, 1}. 4. Вставить между множествами символ Î или Ì так, чтобы получилось истинное высказывание: а) {1} {1, {1, 2}}; б) Æ {Æ}; в) Æ {{Æ}}; г) {1, 2} {1, 2, {1, 2}}. 5. Найти А È В, А Ç В, А \ В, В \ А,` А,` В: а) А = {1, 2, 3}, В = {2, 3, 5, 4}, U = {1, 2, …, 9}; б) А = { х ׀ х делится на 2}, В = { х ׀ х делится на 3}, U = N. 6. Доказать следующие тождества:
7. Показать с помощью диаграмм Эйлера-Венна, какие из следующих утверждений верны:
8. Найти мощность множеств, мощность их булеанов и | А È В | – мощность объединения множеств: а) А = {4, 5, 6}, В = {4, 5, 6, 7, 8}; б) А = {1, 3, 5, 6}, В = {4, 5, 6, 7}; в) А = {3, 5, 7}, В = {2, 5, 6, 7, 9}; г) А = {1, 2, 3, 5}, В = {2, 4, 5, 6, 7}. 9. Вставить между множествами символ Î или Í так, чтобы получилось истинное высказывание: а) {1} {1, {1, 2}}; г) Æ {1, 2, {1}, {Æ}}; б) {1, 2} {1, 2, {1},{2}}; д) Æ {{Æ}}; в) {1, 2} {1, 2,{1, 2}}; е) Æ {Æ}. 10. Привести пример множеств A, B, C, таких, чтобы выполнялись условия: а) A Î B, B Ï C, A Í C; б) A Î B, A Ï C, C Í B; в) A Í B, B Î C, A Ï C. Литература 1. Куликов, Л. Я. Сборник задач по алгебре и теории чисел / Л. Я. Куликов, А. И. Москаленко, А. А Фомин. – М.: Просвещение, 1993. – 288 с. 2. Ерусалимский, Я. М. Дискретная математика. Теория, задачи, приложения: учеб. пособие для вузов / Я. М. Ерусалимский. – М.: Вузовская книга, 2008. – 288 с. 3. Новиков, Ф. А. Дискретная математика для программистов: учебник для вузов / Ф. А. Новиков. – СПб.: Питер, 2001. – 304 с.
Практическое занятие № 2 Тема: «Бинарные отношения» Цель занятия: усвоение таких понятий, как упорядоченная пара, прямое произведение множеств, бинарное отношение, типы бинарных отношений, свойства (рефлексивность, антирефлексивность, симметричность, антисимметричность, транзитивность). Пояснение к работе Время выполнения практического задания – 2 часа. Последовательность выполнения 1. Руководствуясь приведенным теоретическим материалом, ответить на следующие вопросы: Какие способы задания бинарного отношения вы знаете? Что является областью определения бинарного отношения r? Что является областью значений бинарного отношения r? Какое отношение r называется рефлексивным на множестве X? Какое отношение r называется симметричным на множестве X? Главная диагональ матрицы какого отношения содержит только единицы? Для какого отношения r всегда выполняется условие r = r – 1? Для какого отношения r всегда выполняется условие r 2. Дать определение следующих понятий: – бинарное отношение; – композиция отношений. 3. Выполнить задания для аудиторных занятий. 4. Выполнить задания для самостоятельной работы. Свойства отношений Отношение r называется рефлексивным на множестве X, если для любого x Î X выполняется x r x. Из определения следует, что всякий элемент (x, x) Î r. Пример. 1. Пусть X – конечное множество, X = {1, 2, 3} и r = {<1, 1>, <1, 2>, <2, 2>, <3, 1>, <3, 3>}. Отношение r рефлексивно. Если X – конечное множество, то главная диагональ матрицы рефлексивного отношения содержит только единицы. Для данного примера 2. Пусть X – множество действительных чисел и r – отношение равенства. Это отношение рефлексивно, т. к. каждое число равно самому себе. Отношение r называется симметричным на множестве X, если для любых x, y Î X из x r y следует y r x. Очевидно, что r симметрично тогда и только тогда, когда r = r – 1. Пример. 1. Пусть X – конечное множество, X = {1, 2, 3} и r = {<1, 1>, <1, 2>, <1, 3>, <2, 1>, <2, 2>, <3, 1>, <3, 3>}. Отношение r симметрично. Если X – конечное множество, то матрица симметричного отношения симметрична относительно главной диагонали. Тогда 2. Пусть X – множество действительных чисел и r – отношение равенства. Это отношение симметрично, т. к. если x равно y, то и y равно x. Отношение r называется транзитивным на множестве X, если для любых x, y, z Î X из x r y и y r z следует x r z. Одновременное выполнение условий x r y, y r z, x r z означает, что пара < x, z > принадлежит композиции r Пример. Пусть X – конечное множество, X = {1, 2, 3} и r = {<1, 1>, <1, 2>, <2, 3>, <1, 3>}. Отношение r транзитивно, т. к. наряду с парами < x, y >и < y, z >имеется пара< x, z >. Например, наряду с парами <1, 2> и <2, 3> имеется пара <1, 3>. Задания Для аудиторных занятий 1. Перечислить элементы множеств А ´ В, В ´ А:
2. Пусть А, В Í С. Доказать, что А ´ В = (А ´ С) Ç (С ´ В). 3. Пусть А, В, С, D – непустые множества. Доказать следующие тождества:
4. Доказать, что для любых непустых множеств А, В, С из равенства (А ´ В) È (В ´ А) = С ´ С следует, что А = В = С. 5. Перечислить все элементы бинарного отношения r:
6. Для каждого из следующих бинарных отношений, определенных на множестве R, найти область определения, область значений и нарисовать декартову диаграмму, то есть изобразить на плоскости множество всех точек (х, у), таких, что х rу:
7. Для бинарного отношения r между элементами множеств А и В найти область определения D r и область значений R r: А = {1, 2, 3, 4, 5}, В = {{1}, {1, 2}, 3, 4, 5}. 8. Найти r -1, rО r, r - 1 О r, rО r- 1 отношений:
9. Задано бинарное отношение r = {<1, 1>, <3, 4>, <1, 4>, <4, 1>, <4, 3>}. Найти D (r), R (r), r 10. Привести пример отношения нетранзитивного, нерефлексивного и несимметричного. Для самостоятельной работы 1. Перечислить элементы множеств А ´ В, В ´ А:
2. Пусть А = { и, л }. Перечислить элементы множеств А 2, А 3. 3. Определить упорядоченную пару á a, b ñ как множество {{ a }, { a, b }}. Доказать, что á a, b ñ = á c, d ñ тогда и только тогда, когда a = c и b = d. 4. Пусть на плоскости задана декартова система координат. Изобразить на плоскости следующие множества: а) [ a, b ] ´ [ c, d ], где a, b, c, d Î R и a < b, c < d; б) [ a, b ]2. 5. Доказать, что подмножество С множества А ´ В является прямым произведением некоторого подмножества А 1 множества А и подмножества В 1 множества В тогда и только тогда, когда для любых пар á a, b ñ, á c, d ñ из С пары á a, b ñ, á c, d ñ также принадлежат С. 6. Перечислить все элементы бинарного отношения r и нарисовать его график:
7. Для каждого из следующих бинарных отношений, определенных на множестве R, найти область определения, область значений:
8. Какими свойствами обладают следующие бинарные отношения (рефлексивность, симметричность, транзитивность), заданные на R?
9. Привести пример отношения транзитивного, рефлексивного и симметричного. 10. Для каждого из следующих бинарных отношений выяснить, какими свойствами (рефлексивность, симметричность, антисимметричность, транзитивность) оно обладает. Дать обоснование ответа.
Литература 1. Куликов, Л. Я. Сборник задач по алгебре и теории чисел / Л. Я. Куликов, А. И. Москаленко, А. А Фомин. – М.: Просвещение, 1993. – 288 с. 2. Иванов, Б. Н. Дискретная математика. Алгоритмы и программы: учеб. пособие для вузов / Б. Н. Иванов. – М.: Лаборатория базовых знаний, 2002. – 288 с. 3. Новиков, Ф. А. Дискретная математика для программистов: учебник для вузов / Ф. А. Новиков. – СПб.: Питер, 2005. – 304 с.
Практическое занятие № 3 Пояснение к работе Время выполнения практического задания – 2 часа. Последовательность выполнения 1. Руководствуясь приведенным теоретическим материалом, ответить на следующие вопросы: Какими свойствами обладает отношение строгого порядка? Что называется классом эквивалентности? Что называется разбиением множества? 2. Дать определение следующих понятий: – отношение эквивалентности; – отношение строгого порядка; – отношение частичного порядка; – отношение линейного порядка. 3. Привести пример разбиения множества. 4. Выполнить задания для аудиторных занятий. 5. Выполнить задания для самостоятельной работы. Задания Для аудиторных занятий 1. Перечислить всевозможные отношения линейного порядка на множестве {1, 2, 3, 4}. 2. Доказать, что пересечение отношений эквивалентности на множестве Х есть отношение эквивалентности на этом множестве. 3. Будет ли отношением эквивалентности на множестве действительных чисел отношение x ry, задаваемое равенством x 2 + y 2 = 25? 4. Будет ли отношением эквивалентности на множестве действительных чисел отношение x r y, задаваемое равенством x = 2 y? 5. Доказать, что если r – частичный порядок, то r -1 – также частичный порядок. 6. Доказать, что каждое из следующих отношений является отношением эквивалентности, и найти классы эквивалентности: а) пусть А = {1, 2, 3}, на множестве Р (А) задано бинарное отношение х rу Û½ х ½= ½ у ½; б) на множестве N ´ N задано бинарное отношение á a, b ñ r á c, d ñ Û a + d = b + c; в) на множестве R: a r b Û a 2 = b 2; г) на множестве R: a r b Û a - b Î Z. 7. На R задано бинарное отношение a r b Û a 2 + a = b 2 + b. Доказать, что r – отношение эквивалентности. Сколько элементов может содержать класс эквивалентности? Существует ли класс эквивалентности, состоящий из одного элемента? 8. Доказать, что отношение á a, b ñ r á c, d ñ Û a 2 + b 2 = c 2 + d 2 является отношением эквивалентности на множестве R × R. Найти классы эквивалентности и изобразить их на координатной плоскости. 9. Показать, что пересечение отношений эквивалентности, определенных на некотором множестве А, является отношением эквивалентности. Для самостоятельной работы 1. Доказать, что если r – отношение эквивалентности, то r -1 – также отношение эквивалентности. 2. Доказать, что если r – отношение эквивалентности, то истинны следующие утверждения ([ x ]r – класс эквивалентности, порожденный элементом х): а) х Î[ x ]r; б) х r y Û [ x ]r = [ y ]r. 3. Доказать, что отношение делимости на множестве N является отношением порядка. Является ли это отношение линейным порядком? Является ли отношением порядка отношение делимости на множестве Z? 4. Доказать, что отношение х ry Û x / y Ú х < y на множестве N является линейным порядком. 5. Для каких множеств А множество { В (А), Í} является линейно упорядоченным? 6. Пусть А – не пустое конечное множество. На B (А) рассмотрим отношение X rY Û ç X ç£ ç Y ç. Является ли r отношением порядка? 7. На множестве всех отображений R в R рассмотреть отношение f rq Û (" x Î R ç f(x) = 1, q(x) = 1). Является ли r отношением порядка? 8. На множестве всех отображений R в R рассмотреть отношение f rq Û { x Î R ç f(x) = 0} Í { x Î R çg(x) = 0}. Является ли r отношением порядка? 9. Доказать, что отношение á a; b ñ r á c; d ñ Û a < c Ú(a = c Ù b £ d) является линейным порядком на множестве Z ´ Z. 10. По аналогии с упражнением 9 определить линейный порядок на множестве А ´ В, если á А, r 1 ñ и á В, r 2ñ – линейно упорядоченные множества. 11. Перечислить всевозможные линейные порядки на множестве {1, 2}; на множестве {1, 2, 3}. Высказать предположение о числе линейных порядков на множестве из n элементов. 12. Пусть F – множество всех непустых конечных подмножеств множества N. Какие элементы упорядоченного множества á F, Í ñ являются минимальными? Доказать, что á F, Í ñ не содержит максимальных элементов. 13. Привести пример упорядоченного множества, имеющего ровно один максимальный (минимальный) элемент, но не имеющего наибольшего (наименьшего) элемента. 14. Доказать: а) упорядоченное множество содержит не более одного наибольшего (наименьшего) элемента; б) если упорядоченное множество содержит наибольший (наименьший) элемент, то он является единственным максимальным (минимальным) элементом этого множества. Литература 1. Белоусов, А. И. Дискретная математика: учебник / А. И. Белоусов. – М.: МГТУ им. Н. Э. Баумана, 2001. – 744 с. 2. Куликов, Л. Я. Сборник задач по алгебре и теории чисел / Л. Я. Куликов, А. И. Москаленко, А. А Фомин. – М.: Просвещение, 1993. – 288 с. 3. Нефедов, В. Н. Курс дискретной математики: учеб. пособие / В. Н. Нефедов, В. А. Осипова. – М.: Изд-во МАИ, 1992. – 264 с.
Практическое занятие № 4 Пояснение к работе Время выполнения практического задания – 2 часа. Последовательность выполнения 1. Руководствуясь приведенным теоретическим материалом, ответить на следующие вопросы: Как обозначается функция (отображение)? Что является областью определения функции? Что является областью значений функции? Какая функция называется инъективной? Какая функция называется сюръективной? Какая функция называется биективной? В чем заключается понятие однозначности или функциональности? Чему равна композиция двух функций? Какое из отношений является функцией: {<1, 2>, <3, 4>, <4, 4>, <5, 6>}; {<1, 2>, <1, 4>, <4, 4>, <5, 6>}. 2. Дать определение функции. 3. Выполнить задания для аудиторных занятий. 4. Выполнить задания для самостоятельной работы. Функции и отображения Пусть f – отношение на А и В, такое, что "(a, b) Î f и (a, c) Î f Þ b = c. Такое свойство отношений называется однозначностью или функциональностью, а само отношение называется функцией из А в В и обозначается следующим образом: f: A ® B, то есть осуществляется отображение множества А на множество В. Если f: A ® B, то обычно используется префиксная форма записи: b = f(a):= (a, b) Î f. Если b = f(a), то а называют аргументом или прообразом элемента b при функции f, а b – значением функции или образом элемента а при f. Итак, из всех отношений функции выделяются тем, что каждый элемент из области определения имеет единственный образ. Область определения функции: fA:= { a Î A ç$ b Î B, b =f(a)}; область значений функции: fВ:= { b Î B ç$ a Î A, b = f(a)}. Функция f называется: инъективной, если b =f(a 1) и b =f(a 2) Þ а 1 = а 2; сюръективной, если " b Î В $ а Î А b = f(a); биективной, если она инъективна и сюръективна. Примеры: 1. {<1, 2>, <3, 4>, <4, 4>, <5, 6>} – функция, fА = {1, 3, 4, 5}; fВ = {2, 4, 6}; {< x, y >: x, y Î R, y = x 2 } – функция, fА = fВ = (–¥, ¥); {<1, 2>, <1, 4>, <4, 4>, <5, 6>} – отношение, но не функция. 2. Даны три функции, отображающие множество действительных чисел R во множество действительных чисел, fi : R ® R. i = 1, 2, 3: а) функция f1(х) = е х инъективна, но не сюръективна; б) функция f2(х) = х 3 – х сюръективна, но не инъективна; в) функция f3(х) = 2 х + 1 биективна. Композиция двух функций есть функция. При этом, если f: Х ® У, g: Y ® Z, то g O f: Х ® Z. Задания Для аудиторных занятий 1. Привести примеры отображений:
2. Найти f(A), где А = {(х, у)Î R ´ R | у = 2 х + 3 }, для следующих отображений:
3. Для каждого из следующих отображений исследовать, является ли оно инъективным, сюръективным:
4. Указать все сюръективные отображения множества А = {1, 2, 3} на множество В ={ а, b }. Существуют ли инъективные отображения А в В? 5. Пусть А и В – конечные множества, | А | = m, | B | = n. a) сколько существует бинарных отношений между элементами множеств А и В? б) сколько существует отображений из А в В? 6. Пусть a: х ® х 2; b: х ® х 3 – отображения R ® R. Найти a 7. Для каждого из следующих бинарных отношений исследовать, является ли оно всюду определенным и функциональным:
8. Доказать, что каждое из следующих бинарных отношений является отображением R в R:
9. Для каждого из следующих бинарных отношений исследовать, является ли оно всюду определенным, функциональным; ответ обосновать. а) б) в) 10. Пусть А и В – конечные множества, ½ А ½ = ½ В ½ = n. а) сколько существует бинарных отношений между элементами множеств А и В? б) сколько существует отображений А в В? Для самостоятельной работы 1. Привести примеры отображений:
2. Найти f(A), где А = {(х, у)Î R ´ R | у = 2 х + 3}, для следующих отображений:
3. Для каждого из следующих отображений исследовать, является ли оно инъективным, сюръективным:
4. Пусть А и В – конечные множества, | А | = m, | B | = n. а) при каких m и n существует инъективное отображение А в В? б) при каких m и n существует биекция А на В? в) пусть существуют биекции А на А ’ и В на В ’. Доказать, что существует биекция А ´ В на А ’ ´ В ’. 5. Для каждого из следующих бинарных отношений исследовать, является ли оно всюду определенным и функциональным:
6. Доказать, что каждое из следующих бинарных отношений является отображением R в R:
7. Для каждого из следующих бинарных отношений исследовать, является ли оно всюду определенным, функциональным; ответ обосновать. а) {á х, у ñ Î N ´ N | x < у £ х + 1}; б) {á х, у ñ Î N ´ N | x / у }; в) {á х, у ñ Î N ´ N | x = у 2}. 8. Указать все сюръективные отображения множества А = {1, 2, 3} на множество B = {a, b}. Существуют ли инъективные отображения А в В? 9. Найти все отображения множества А = {1, 2} в себя, укажите, какие из них инъективные, сюръективные. 10. Пусть f – отображение конечного множества А в себя. Докажите, что f инъективно тогда и только тогда, тогда f сюръективно. Литература | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

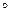 r Í r.
r Í r.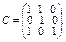
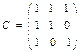 .
.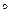 r. Поэтому для транзитивности r необходимо и достаточно, чтобы множество r
r. Поэтому для транзитивности r необходимо и достаточно, чтобы множество r 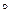 r являлось подмножеством r, т. е. r
r являлось подмножеством r, т. е. r 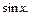
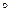 r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?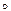 a.
a.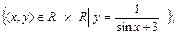
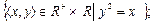
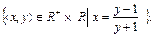
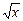 ;
;
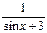 }.
}.



