
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: «Переключательные (булевы) функции»Содержание книги
Поиск на нашем сайте Цель занятия: усвоение таких понятий, как булевы функции, формулы логики булевых функций, булева алгебра, замкнутые классы. Пояснение к работе Время выполнения практического задания – 4 часа. Последовательность выполнения 1. Руководствуясь приведенным теоретическим материалом, ответить на следующие вопросы: Как реализуется табличное представление булевой функции? Что является важнейшей интерпретацией теории булевых функций? Какие существуют элементарные булевы функции двух переменных? Как задается функция вектором ее значений? Какие булевы функции называются равными? Какая система булевых функций называется полной? 2. Дать определение следующих понятий: – булева функция; – фиктивная и существенная переменная; – булева алгебра (алгебра логики). 3. Записать булеву функцию в виде произвольного отображения. 4. Выполнить задания для аудиторных занятий. 5. Выполнить задания для самостоятельной работы. 10.1. Основные определения Булевой функцией f (x 1, x 2,..., xn) называется произвольная функция n переменных, аргументы которой x 1, x 2,..., xn и сама функция f принимают значения 0 или 1, т. е. xi Одной из важнейших интерпретаций теории булевых функций является теория переключательных функций. Первоначально математический аппарат теории булевых функций был применен для анализа и синтеза релейно-контактных схем с операциями последовательного и параллельного соединения контактов. Любая булева функция может быть представлена таблицей, в левой части которой перечислены все наборы переменных (2 n), а в правой части – значения функции. Для формирования столбца значений переменных удобен лексикографический порядок, в соответствии с которым каждый последующий набор значений получается из предыдущего прибавлением 1 в двоичной системе счисления. Функций одной переменной четыре. Из них выделим функцию “отрицание x ” (обозначается Ø x). Булевых функций двух переменных – 16. Те из них, которые имеют специальные названия (элементарные функции), представлены в табл. 2. Таблица 2
Остальные функции специальных названий не имеют и могут быть выражены через перечисленные выше функции.
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 191; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

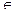 {0, 1}, i = 1, 2,..., n; f (x 1, x 2, ..., xn)
{0, 1}, i = 1, 2,..., n; f (x 1, x 2, ..., xn) 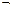 x 2 ;
x 1→ x 2
x 2 ;
x 1→ x 2



