Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: «Функции и отображения»Содержание книги
Поиск на нашем сайте
Цель занятия: усвоение таких понятий, как функция, отображение, область определения и область значений функции, инъекция, сюръекция, биекция. Пояснение к работе Время выполнения практического задания – 2 часа. Последовательность выполнения 1. Руководствуясь приведенным теоретическим материалом, ответить на следующие вопросы: Как обозначается функция (отображение)? Что является областью определения функции? Что является областью значений функции? Какая функция называется инъективной? Какая функция называется сюръективной? Какая функция называется биективной? В чем заключается понятие однозначности или функциональности? Чему равна композиция двух функций? Какое из отношений является функцией: {<1, 2>, <3, 4>, <4, 4>, <5, 6>}; {<1, 2>, <1, 4>, <4, 4>, <5, 6>}. 2. Дать определение функции. 3. Выполнить задания для аудиторных занятий. 4. Выполнить задания для самостоятельной работы. Функции и отображения Пусть f – отношение на А и В, такое, что "(a, b) Î f и (a, c) Î f Þ b = c. Такое свойство отношений называется однозначностью или функциональностью, а само отношение называется функцией из А в В и обозначается следующим образом: f: A ® B, то есть осуществляется отображение множества А на множество В. Если f: A ® B, то обычно используется префиксная форма записи: b = f(a):= (a, b) Î f. Если b = f(a), то а называют аргументом или прообразом элемента b при функции f, а b – значением функции или образом элемента а при f. Итак, из всех отношений функции выделяются тем, что каждый элемент из области определения имеет единственный образ. Область определения функции: fA:= { a Î A ç$ b Î B, b =f(a)}; область значений функции: fВ:= { b Î B ç$ a Î A, b = f(a)}. Функция f называется: инъективной, если b =f(a 1) и b =f(a 2) Þ а 1 = а 2; сюръективной, если " b Î В $ а Î А b = f(a); биективной, если она инъективна и сюръективна. Примеры: 1. {<1, 2>, <3, 4>, <4, 4>, <5, 6>} – функция, fА = {1, 3, 4, 5}; fВ = {2, 4, 6}; {< x, y >: x, y Î R, y = x 2 } – функция, fА = fВ = (–¥, ¥); {<1, 2>, <1, 4>, <4, 4>, <5, 6>} – отношение, но не функция. 2. Даны три функции, отображающие множество действительных чисел R во множество действительных чисел, fi : R ® R. i = 1, 2, 3: а) функция f1(х) = е х инъективна, но не сюръективна; б) функция f2(х) = х 3 – х сюръективна, но не инъективна; в) функция f3(х) = 2 х + 1 биективна.
Композиция двух функций есть функция. При этом, если f: Х ® У, g: Y ® Z, то g O f: Х ® Z. Задания Для аудиторных занятий 1. Привести примеры отображений:
2. Найти f(A), где А = {(х, у)Î R ´ R | у = 2 х + 3 }, для следующих отображений:
3. Для каждого из следующих отображений исследовать, является ли оно инъективным, сюръективным:
4. Указать все сюръективные отображения множества А = {1, 2, 3} на множество В ={ а, b }. Существуют ли инъективные отображения А в В? 5. Пусть А и В – конечные множества, | А | = m, | B | = n. a) сколько существует бинарных отношений между элементами множеств А и В? б) сколько существует отображений из А в В? 6. Пусть a: х ® х 2; b: х ® х 3 – отображения R ® R. Найти a 7. Для каждого из следующих бинарных отношений исследовать, является ли оно всюду определенным и функциональным:
8. Доказать, что каждое из следующих бинарных отношений является отображением R в R:
9. Для каждого из следующих бинарных отношений исследовать, является ли оно всюду определенным, функциональным; ответ обосновать. а) б) в) 10. Пусть А и В – конечные множества, ½ А ½ = ½ В ½ = n. а) сколько существует бинарных отношений между элементами множеств А и В? б) сколько существует отображений А в В? Для самостоятельной работы 1. Привести примеры отображений:
2. Найти f(A), где А = {(х, у)Î R ´ R | у = 2 х + 3}, для следующих отображений:
3. Для каждого из следующих отображений исследовать, является ли оно инъективным, сюръективным:
4. Пусть А и В – конечные множества, | А | = m, | B | = n. а) при каких m и n существует инъективное отображение А в В? б) при каких m и n существует биекция А на В? в) пусть существуют биекции А на А ’ и В на В ’. Доказать, что существует биекция А ´ В на А ’ ´ В ’.
5. Для каждого из следующих бинарных отношений исследовать, является ли оно всюду определенным и функциональным:
6. Доказать, что каждое из следующих бинарных отношений является отображением R в R:
7. Для каждого из следующих бинарных отношений исследовать, является ли оно всюду определенным, функциональным; ответ обосновать. а) {á х, у ñ Î N ´ N | x < у £ х + 1}; б) {á х, у ñ Î N ´ N | x / у }; в) {á х, у ñ Î N ´ N | x = у 2}. 8. Указать все сюръективные отображения множества А = {1, 2, 3} на множество B = {a, b}. Существуют ли инъективные отображения А в В? 9. Найти все отображения множества А = {1, 2} в себя, укажите, какие из них инъективные, сюръективные. 10. Пусть f – отображение конечного множества А в себя. Докажите, что f инъективно тогда и только тогда, тогда f сюръективно. Литература 1. Куликов, Л. Я. Сборник задач по алгебре и теории чисел / Л. Я. Куликов, А. И. Москаленко, А. А Фомин. – М.: Просвещение, 1993. – 288 с. 2. Новиков, Ф. А. Дискретная математика для программистов: учебник для вузов / Ф. А. Новиков. – СПб.: Питер, 2001. – 304 с.
Практическое занятие № 5 Тема: «Элементы графа. Способы задания графа. Подграфы. Изоморфизм» Цель занятия: усвоение таких понятий, как граф, вершины и ребра графа, ориентированный и неориентированный граф, мультиграф, псевдограф, смежность, инцидентность, изоморфизм, матрицы смежности и инцидентности, двудольный граф, полный граф, подграф, степень вершины. Пояснение к работе Время выполнения практического задания – 2 часа. Последовательность выполнения 1. Руководствуясь приведенным теоретическим материалом, ответить на следующие вопросы: Какие вершины графа называются смежными? В чем заключается понятие инцидентности? Как задается матрица инциденций для орграфа? Какой граф называется псевдографом? Какой граф называется двудольным? 2. Дать определение следующих понятий: – граф; – изоморфизм; – полный граф; – подграф; – ориентированный граф. 3. Выполнить задания для аудиторных занятий. 4. Выполнить задания для самостоятельной работы. Элементы графа Граф G – это совокупность двух множеств: непустого множества вершин V = { v 1, v 2,..., vn } и множества ребер (дуг) Е = { е 1, е 2,..., еn }. Таким образом, G = (V, Е), V ¹ Æ, Е Ì V × V. Если (v 1, v 2) – упорядоченная пара (т. е. дуга), то v 1 называется началом, a v 2 – концом дуги е. Если { v 1, v 2} – неупорядоченная пара, то ребро е называется неориентированным. Всякому графу G можно поставить в соответствие соотнесенный неориентированный граф G с теми же множествами V и Е и инцидентностями, но все пары неупорядоченные. Такой граф называется ассоциированным. Вершина, не инцидентная ни одному ребру, называется изолированной. Вершина, инцидентная ровно одному ребру, и само это ребро называются концевыми или висячими. Ребро с совпадающими концами называется петлей. Две вершины, инцидентные одному и тому же ребру, называются смежными. Два ребра, инцидентные одной и той же вершине, называются смежными. Ребра, которым поставлена в соответствие одна и та же пара вершин, называются кратными или параллельными.
Граф, содержащий кратные ребра, называется мультиграфом. Неориентированное ребро графа эквивалентно двум противоположно направленным дугам, соединяющим те же самые вершины. Граф с кратными ребрами и петлями называется псевдографом.

Рис. 3 На рис. 3 изображены: ориентированный псевдограф, имеющий 7 вершин и 6 дуг, и неориентированный мультиграф, имеющий 4 вершины и 5 ребер. Проиллюстрируем некоторые введенные понятия. Для орграфа (рис. 3 а): v 1, v 2, v 3, v 4, v 5, v 6, v 7 – вершины (узлы); v 5 – изолированная вершина; v 1, v 4 – концевые (висячие) вершины; v 2 и v 3, v 2 и v 1 –пары соседних вершин; е 1, е 2, е 3, е 4, е 5, е 6 – ориентированные ребра (дуги); е 2 и е 3 – параллельные (кратные) дуги; е 2 и е 1 – смежные дуги; е 6 –петля для орграфа. Для графа (рис. 3 б): v 1, v 2, v 3, v 4 – вершины; v 4 – концевая (висячая) вершина; v 2 и v 3, v 2 и v 1 –пары соседних вершин; е 1, е 2, е 3, е 4, е 5 – ребра (дуги); е 4 и е 5 – параллельные (кратные) ребра; е 2 и е 3 – смежные ребра; петель нет. 5.2. Способы задания графов 1. Перечисление (список) ребер графа с указанием их концов и добавлением списка изолированных вершин. 2. Матрица смежности A = ( aij)определяется одинаково для ориентированного и неориентированного графов. Это квадратная матрица порядка n, где n – число вершин, у которой aij = Матрицей инцидентности B = (bij) ориентированного графа называется матрица (n ´ m), где n – число вершин, m – число ребер, у которой bi j = Для неориентированного графа матрица инцидентности B задается следующим образом: bi j = Петле соответствует элемент, равный 2. Пример. Матрицы смежности и инцидентности графа, изображенного на рис. 3 а, имеют вид (рис. 4):
Рис. 4 3. Для наглядности граф представляют в виде геометрического объекта: вершинам соответствуют различные выделенные точки в пространстве (на плоскости), ребрам – отрезки кривых, связывающие вершины. Рассмотрим некоторые разновидности графов. Неориентированный граф G = (V, E) – двудольный, если множество его вершин V можно разбить на два такие подмножества V 1и V 2, что каждое ребро имеет один конец в V 1, а другой в V 2. Если же каждая из вершин класса V 1 связана ребром с каждой вершиной класса V 2, то граф называется полным двудольным и обозначается К m,n, где m =| V 1|, n =| V 2|. На рис. 5 а изображен двудольный граф, на рис. 5 б и 5 в – полные двудольные графы К 3,2 и К 3,3 . Пример.
а б в Рис. 5
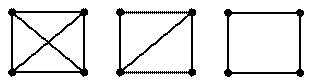
Полным графом называется граф без кратных ребер (и иногда без петель), в котором любые две вершины соединены ребром (ориентированным или неориентированным). Полный неориентированный граф с n вершинами обозначается К n. Очевидно, граф К n содержит n (n - 1)/2 ребер. На рис. 6 а, 6 б и 6 в изображены графы К 3, К 4, К 5, соответственно. На рис. 6 г также изображен полный граф.
а б в г Рис. 6 Подграфы Граф G ¢ = (V ¢, E ¢) называется подграфом графа G = (V, Е), обозначение: G ¢ Í G, если V ¢ Í V, Е ¢ Í Е и для множеств V ' и Е' сохраняются инциденции графа G. При этом, очевидно, каждое ребро из Е ' входит в подграф G ¢ вместе со своими концами. Подграф называется собственным, если он отличен от самого графа. Пример. Графы на рис. 7 б и 7 в являются подграфами графа на рис. 7 а.
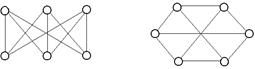
а б в Рис. 7 Изоморфизм графов Два графа G 1 = (V 1, E 1) и G 2 = (V 2, E 2) изоморфны, если между их вершинами существует взаимно однозначное соответствие j: V 1 ® V 2 такое, что для любой пары вершин u, v из V 1 ребро (u, v) Î Е1 «ребро (j(u), j(v)) Î Е2. Пример. Графы, изображенные на рис. 8, являются изоморфными.
Рис. 8 Изоморфные графы отличаются только нумерацией вершин. Матрицы смежности двух изоморфных графов могут быть получены одна из другой перестановкой строк и столбцов. Чтобы узнать, являются ли два графа изоморфными, нужно произвести все возможные перестановки строк и столбцов матрицы смежности одного из графов. Если после какой-нибудь перестановки получится матрица смежности второго графа, то эти графы изоморфны. Чтобы убедиться, что графы неизоморфны, надо выполнить все n! возможных перестановок строк и столбцов. Степени вершин графа Степенью вершины v графа G называется число d(v) ребер графа G, инцидентных вершине v. Вершина графа, имеющая степень 0, называется изолированной, а степень 1 – висячей. В случае неориентированного псевдографа считается, что вклад каждой петли, инцидентной некоторой вершине v, в d(v) равен 2 (тогда как вклад любого другого ребра, инцидентного вершине v, равен 1). Полустепенью исхода (захода) вершины v орграфа D называется число d+(v) (d-(v)) дуг орграфа D, исходящих из вершины v (входящих в вершину v). В случае ориентированного псевдографа вклад каждой петли, инцидентной некоторой вершине v, в d(v) равен 1, как в d+(v), так и в d-(v). Пример. В графе G (рис. 3 б) степень вершины v 1 равна четырем, т. е. d(v 1) = 4; вершина v 4 – висячая, так как d(v 4) = 1. В ориентированном псевдографе (рис. 3 а) степень вершины v 6 равна трем, т. е. d(v 6) = d+(v 6) + (d-(v 6) = 2 + 1 = 3; вершина v 1 – висячая, так как d(v 1) = 1, вершина v 5 – изолированная, так как d(v 5) = 0. Задания Для аудиторных занятий 1. Даны реализации графов (рис. 9). Какие это графы? Описать их основные характеристики. Привести примеры элементов графов.
а) б) в)
Рис. 9 2. Записать матрицы смежности и инцидентности для неориентированного графа (рис. 9 а). 3. Записать матрицы смежности и инцидентности для ориентированного графа (рис. 9 б). 4. Изобразить ассоциированный граф для заданного графа (рис. 9 б). 5. Изобразить все попарно неизоморфные 4-вершинные графы без петель и кратных ребер. Записать для них матрицы смежности и инцидентности. 6. Построить все попарно неизоморфные 5-вершинные графы, не имеющие петель, кратных ребер и изолированных вершин. 7. Какое из двух утверждений верно: а) ориентированный граф является частным случаем неориентированного графа; б) неориентированный граф является частным случаем ориентированного графа. 8. Перечислить все возможные способы задания графов. 9. Всегда ли матрица смежности симметрична относительно главной диагонали? 10. Как по матрице смежности определить число ребер неориентированного графа? Для самостоятельной работы 1. Как по матрице инцидентности, не рисуя граф, определить его матрицу смежности? 2. Может ли матрица 3. Какие из следующих утверждений являются правильными: а) если матрица смежности несимметричная, то граф ориентированный; б) если граф неориентированный, то матрица смежности симметричная; в) если диагональные элементы матрицы смежности – нули, то граф неориентированный? 4. Записать матрицы смежности и инцидентности для ориентированного графа (рис. 9 в). 5. Изобразить все попарно неизоморфные ориентированные псевдографы, содержащие: а) 2 вершины и 2 дуги; б) 3 вершины и 4 дуги; в) 4 вершины и 3 дуги. 6. Изобразить ассоциированный граф для заданного графа (рис. 9 в). 7. Чему равны степени вершин для ориентированного и неориентированного графов? 8. Определить степени вершин орграфа (рис. 3 а). Есть ли в заданном графе изолированные и висячие вершины? 9. Определить степени вершин в заданных графах (рис. 9). 10. Даны реализации графов (рис. 9). Какие это графы? Привести примеры смежных вершин и смежных ребер. Литература 1. Новиков, Ф. А. Дискретная математика для программистов: учебник для вузов / Ф. А. Новиков. – СПб.: Питер, 2001. – 304 с. 2. Нефедов, В. Н. Курс дискретной математики: учеб. пособие / В. Н. Нефедов, В. А. Осипова. – М.: Изд-во МАИ, 1992. – 264 с. 3. Акимов, О. Е. Дискретная математика. Логика, группы, графы. – 2-е изд., доп. / О. Е. Акимов. – М.: Лаборатория базовых знаний, 2001. – 367 с. Практическое занятие № 6 Тема: «Путь в графе. Поиск путей (маршрутов)» Цель занятия: усвоение таких понятий, как маршрут, цепь и цикл графа, образ, прообраз вершин графа, минимальный путь в графе, эйлеровы графы. Пояснение к работе Время выполнения практического задания – 2 часа. Последовательность выполнения 1. Руководствуясь приведенным теоретическим материалом, ответить на следующие вопросы: В чем состоит алгоритм поиска путей с минимальным числом дуг? Какой цикл называется эйлеровым? Каков критерий существования эйлерова цикла в графе? Каков критерий существования эйлеровой цепи в графе? 2. Дать определение следующих понятий: – маршрут в графе (привести пример); – цепь и простая цепь в графе; – цикл и простой цикл в графе; – эйлеровой цепь; – матрица смежности графа; – степень вершины графа. 3. Выполнить задания для аудиторных занятий. 4. Выполнить задания для самостоятельной работы. Маршруты, цепи, циклы Маршрутом в графе G = (V, E) (путем в графе D = (V, E)) называется последовательность вершин и рёбер (дуг) вида v 0, e 1, v 1, e 2,..., v n-1, e n, v n, где v i Î V, i Î [0, n ], e i Î E, (v i-1, e i), (v i, e i) Î I, i Î [1, n ]. Вершины v 0, v n называются связанными данным маршрутом (или просто связанными). Вершину v 0 называют началом, а v n – концом маршрута. Если v 0 = v n, то маршрут называют замкнутым. Число n называется длиной маршрута. Маршрут, в котором все рёбра попарно различны, называется цепью. Замкнутый маршрут, являющийся цепью, называется циклом (контуром). Цепь, в которой все вершины попарно различны, называется простой цепью. Цикл, в котором все вершины, кроме первой и последней, попарно различны, называется простым циклом. Примеры: 1. Последовательность v 1, e 1, v 2, e 3, v 4, e 4, v 3 – маршрут длины 3, соединяющий вершины v 1, v 3 в графе G (рис. 11); это простая цепь, так как все ребра и вершины попарно различны. 2. v 2, e 3, v 2 – простой контур длины 1 в ориентированном псевдографе D (рис. 10). 3. v 1, e 2, v 2, e 4, v 3 – путь из v 1 в v 3 длины 2 в ориентированном псевдографе D (рис. 10); это простая цепь, так как все дуги и вершины попарно различны.
Рис. 10 Рис. 11 6.2. Поиск путей (маршрутов)с минимальным числом дуг При решении некоторых прикладных задач нередко возникает необходимость найти минимальный маршрут, соединяющий заданные вершины в графе. Приведем алгоритм решения этой задачи. Путь в орграфе D из вершины v в вершину w (v ¹ w) называется минимальным, если он имеет минимальную длину среди всех путей орграфа D из вершины v в вершину w. Аналогично определяется минимальный маршрут в графе G. Алгоритм нахождения минимального маршрута состоит из следующих шагов: Шаг 1. Помечаем вершину v индексом 0. Затем помечаем вершины, принадлежащие образу вершины v, индексом 1. Множество вершин с индексом 1 обозначаем FW1(v). Полагаем k = 1. Шаг 2. Если FWk(v) = Æ или выполняется k = n – 1, w Ï FWk(v), то вершина w не достижима из v и работа алгоритма на этом заканчивается. В противном случае переходим к шагу 3. Шаг 3. Если w Ï FWk(v), то переходим к шагу 4. В противном случае существует путь из v в w длины k, и этот путь является минимальным. Последовательность вершин v w 1 w 2 … wk -1 w , где wk -1 Î FWk-1(v) Ç D-1(w); wk -2 Î FWk-2(v) Ç D-1(w л-1); … w 1 Î FW1(v) Ç D-1(w 2) и есть искомый минимальный путь из v в w. На этом работа алгоритма заканчивается. Шаг 4. Помечаем индексом k + 1 все непомеченные вершины, которые принадлежат образу множества вершин с индексом k. Множество вершин с индексом k + 1 обозначаем FWk+1(v). Присваиваем k:= k + 1 и переходим к шагу 2. Пример. Используя предложенный алгоритм, определим минимальный путь из v 1 в v 6 в орграфе D, заданном матрицей смежности, представленной в табл. 1.
Таблица 1
Действуя согласно алгоритму, последовательно определяем FW1(v 1) = { v 4, v 5 }; FW2(v 1) = D(FW1(v 1))\{ v 1, v 4, v 5 } ={ v 2, v 3 }; FW3(v1) = D(FW2(v1))\{ v1, v2, v3, v4, v5 } = { v6 }. Таким образом, v 6 Î FW3(v 1), а значит (см. шаг 3) существует путь из v 1 в v 6 длины 3 и этот путь является минимальным. Найдем теперь минимальный путь из v 1 в v 6. Определим множество FW2(v 1) Ç D-1(v 6) = { v 2, v 3 } Ç { v 2, v 3 } = { v 2, v 3 }. Выберем любую вершину из найденного множества, например вершину v 3. Определим далее множество FW1(v 1) Ç D-1(v 3) = { v 4, v 5 } Ç { v 4, v 5, v 6 = { v 4, v 5 }. Выберем любую вершину из найденного множества, например, вершину v 5. Тогда v 1 v 5 v 3 v 6 – искомый минимальный путь из v 1 в v 6 длины 3 в орграфе D. Эйлеровы графы Пусть G – псевдограф. Цепь (цикл) в G называется эйлеровой, если она (он) проходит по одному разу через каждое ребро псевдографа G.
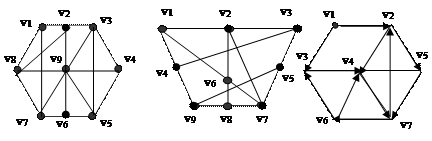
щий эйлеров цикл, тоже будем называть эйлеровым. В любом эйлеровом графе степени всех вершин чётные. Пусть по некоторой вершине v цикл проходит k раз. Но так как перед этой вершиной и после неё цикл должен проходить по инцидентным ей рёбрам, то количество рёбер, инцидентных данной вершине, по которым проходит цикл – 2 k. Так как цикл эйлеров – рёбер, по которым цикл не проходит, нет, значит 2 k – степень вершины v. Если в связном графе степени всех вершин чётные, то в графе существует эйлеров цикл. В ходе доказательства мы дадим алгоритм построения такого цикла. Начнём с произвольной вершины v и будем строить из неё цепь, пока есть возможность её продолжить. Пусть в какой-то момент построения мы находимся в вершине u (не совпадающей с v). Тогда цепь, которую мы построили, проходит по нечётному числу рёбер, инцидентных данной вершине. Степень вершины u чётная, следовательно, есть хотя бы одно ребро, инцидентное вершине u, по которому цепь не прошла – значит её можно продолжить. Следовательно, цепь может закончится только в вершине v. Получим цикл. В задачах часто возникает необходимость нахождения цепи, проходящей по каждому ребру ровно один раз (снимается требование замкнутости). Такие цепи будем называть эйлеровыми цепями. Задания Для аудиторных занятий 1. Задан граф G (рис. 13 а). Найти путь с минимальным числом ребер из вершины v 1 в вершину v 6 графа G.
а б в
а б в Рис. 13 2. Для графа G (рис. 13 б) записать матрицу смежности и найти путь с минимальным числом ребер из вершины v 2 в вершину v 9. 3. Для орграфа D (рис. 13 в) записать матрицу смежности и найти путь с минимальным числом ребер из вершины v 1 в вершину v 7. 4. Определить, содержит ли граф на рис. 13 а эйлеров цикл или эйлерову цепь. 5. Может ли вершина, входящая в цикл графа, иметь степень, меньшую двух? 6. Как называется путь, у которого начало первой дуги совпадает с концом последней? 7. Как называется маршрут, у которого первая вершина совпадает с последней? 8. Показать, что в любом графе количество вершин нечетной степени четно. 9. Показать, что из всякого замкнутого маршрута нечетной длины можно выделить простую цепь. 10. Показать, что ребро, входящее в цикл графа, входит в некоторый его простой цикл. Для самостоятельной работы 1. Задан граф G (рис. 13 а). Найти путь с минимальным числом ребер из вершины v 1 в вершину v 7 графа G. 2. Для графа G (рис. 13 б) записать матрицу смежности и найти путь с минимальным числом ребер из вершины v 1 в вершину v 8. 3. Для графа G (рис. 13 б) записать матрицу инцидентности. 4. Для орграфа D (рис. 13 в) записать матрицу смежности и найти путь с минимальным числом ребер из вершины v 1 в вершину v 6. 5. Показать, что любая вершина, входящая в цикл, не является висячей. 6. Доказать, что если в орграфе отсутствуют вершины с нулевой полустепенью исхода (захода), то в орграфе имеется простой контур. 7. Доказать, что удаление из орграфа вершины v с d+(v) ≤ 1 (d-(v) ≤ 1) приводит к орграфу, контуры которого совпадают с контурами исходного орграфа. 8. Привести определение простой цепи: а) цепь, в которой вершины и ребра повторяются; б) чередование вершин и ребер; в) цепь, в которой все вершины попарно различны. 9. В чем заключается понятие смежности? а) сежными являются вершины, инцидентные одному ребру; б) смежными являются два ребра, не имеющие общих вершин; в) смежными являются вершины, соединенные некоторым маршрутом. 10. Задан псевдограф G. Цепь в G называется эйлеровой, если… а) она проходит по одному разу через каждую точку псевдографа; б) она проходит по одному разу через каждое ребро псевдографа; в) она проходит по одному разу через вершины и ребра. Литература 1. Новиков, Ф. А. Дискретная математика для программистов: учебник для вузов / Ф. А. Новиков. – СПб.: Питер, 2001. – 304 с. 2. Акимов, О. Е. Дискретная математика. Логика, группы, графы. – 2-е изд., доп. / О. Е. Акимов. – М.: Лаборатория базовых знаний, 2001. – 367 с.
Практическое занятие № 7
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 390; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.212.203 (0.016 с.) |

 b и b
b и b  a.
a.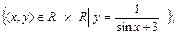
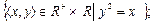
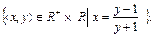
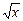 ;
;
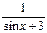 }.
}.
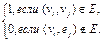
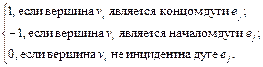

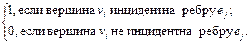
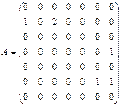
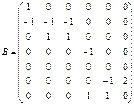 .
.


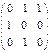 быть матрицей смежности неориентированного графа?
быть матрицей смежности неориентированного графа?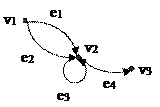

 Рис. 12
Рис. 12