
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Полные системы булевых функцийСодержание книги
Поиск на нашем сайте
Как известно, алгеброй называют систему, включающую в себя некоторое непустое множество объектов с заданными на нем функциями (операциями), результатами применения которых к объектам данного множества являются объекты того же множества. Булевой алгеброй илиалгеброй логики называется двухэлементное множество B = {0, 1} вместе с операциями конъюнкции, дизъюнкции и отрицания. Система булевых функций { f 1, f 2, …, fn } называется полной, если любая булева функция может быть выражена в виде суперпозиции этих функций. Все логические операции могут быть выражены через операции конъюнкции, дизъюнкции и отрицания. Поэтому система функций {Ø, &, Ú} является полной. Также полными являются следующие системы функций: а) {Ø, Ú}; б) {Ø, &}; в) {Ø, É}. Полнота систем {Ø, Ú} и {Ø, &} следует из полноты системы {Ø, &, Ú}, а также законов де Моргана и двойного отрицания, следствием которых является возможность выразить конъюнкцию через дизъюнкцию и наоборот: A & B ºØ(Ø A Ú Ø B); A Ú B º Ø(Ø A & Ø B). Поэтому система {Ø, &, Ú} может быть сокращена на одну функцию. Полнота системы {Ø, É} следует из полноты системы {Ø, Ú} и равносильности, позволяющей выразить импликацию через отрицание и дизъюнкцию: A É B ºØ A Ú B. Пусть дан класс функций B (т. е. конечное или бесконечное множество функций), объединенных по общему признаку. Замыканием этого класса (обозначение – [B]) будем называть множество всех суперпозиций функций из класса B. Класс B будем называть замкнутым, если его замыкание совпадает с ним самим B = [B]. Рассмотрим классы функций, которые являются замкнутыми. Класс Т0 – класс функций, сохраняющих константу 0. f( Класс Т1 – класс функций, сохраняющих константу 1. f( Класс S – класс самодвойственных функций. f( Функция Класс М – класс монотонных функций. f( На множестве наборов значений переменных
Класс L – класс линейных функций. f( Теорема Поста. Система функций полна тогда и только тогда, когда она не находится ни в одном из пяти важнейших замкнутых классов, а именно S, M, L, T0, T1. Пример. Исследовать полноту системы А = {f1 = x Å y, f2 = xy Å z, f3 = x Å y Å z Å 1, f4 = xy Å yz Å zx }(табл. 4). Решение. Результаты исследования на принадлежность функций каждому из пяти классов отображены в критериальной таблице (табл. 5). Таблица 5
а) f1, f2, f4 Î Т0, т. к. f1(0, 0) = 0 Å 0 = 0, f2(0, 0) = 0 Ù 0 Å 0 = 0, f4(0, 0, 0) = 0 Ù 0 Å 0 Ù 0 Å 0 Ù 0 = 0; f3 Ï Т0, т. к. f3(0, 0, 0) = 0 Å 0 Å 0 Å 1 = 1; б) f1, f2, f3ÏТ1, т. к. f1(1,1) = 1Å1= 0, f2(1,1) = 1Ù1Å1 = 0, f3(1, 1,1) = 1 Å 1 Å 1 Å 1 = 0; f4 ÎТ1, т. к. f4(1, 1, 1) = 1 Ù 1 Å 1 Ù 1 Å 1 Ù 1 = 1; в) f1, f3 Î L, т. к. f1 = x Å y, f3 = x Å y Å z Å 1 – представимы полиномом Жегалкина первой степени; f2, f4 Ï L, т. к. f2 = xy Å z, f4 = xy Å yz Å zx – представимы полиномом Жегалкина второй степени; г) f3, f4 Î S, т. к. f3*( f1, f2 Ï S, т. к. f1*( f2*( д) f1, f2, f3 Ï М, т. к. f1: (0, 0, 1, 1) Вывод: система функций А является полной, т. к. в каждом из столбцов критериальной таблицы есть хотя бы один «–». Задания Для аудиторных занятий 1. Построив таблицы для соответствующих функций, записать их в векторной форме. Выяснить, эквивалентны ли формулы f и g: а) f = x Ú y ~ х и g = (x ® y) Ù y; б) f = x (y ® z) и g = x ® (y ç zx). 2. С помощью табличного представления задать значения следующих булевых функций: а) f( в) f( г) f( 3. С помощью векторного представления задать значения следующих булевых функций: а) f( б) f( 4. Указать все фиктивные переменные у функции f:
а) f( в) f( г) f( д) f( 5. Указать все фиктивные и существенные переменные у функции f: а) f( в) f( г) f( 6. Перечислить существенные переменные у следующих функций: а) f( б) f( 7. Какие значения принимает булева функция двух переменных для x 1 Å x 2?Как называется эта функция? 8. Выяснить, является ли самодвойственной и монотонной функция f: f = x 1 x 2 Ú x 1 x 3 Ú x 3 x 2. 9. Выяснить, полна ли система функций: А = { xy, x Ú y, x Å y Å z Å 1}. Для самостоятельной работы 1. Построив таблицы для соответствующих функций, записать их в векторной форме. Выяснить, эквивалентны ли формулы f и g: а) f = xy ® х и g = xy ® y; б) f = xy Ù z и g = x ® (y ç zx). 2. С помощью табличного представления задать значения следующих булевых функций: а) f( в) f( г) f( 3. Указать все фиктивные переменные у функции f: а) f( в) f( 4. Указать все фиктивные и существенные переменные у функции f: а) f( в) f( г) f( 5. Перечислить существенные переменные у следующих функций. а) f( б) f( 6. С помощью векторного представления задать значения следующих булевых функций: а) f( б) f( 7. Какие значения принимает булева функция двух переменных для x 1 Å x 2? Как называется эта функция? 8. Выяснить, является ли самодвойственной и монотонной функция f f = x 1 ® x 2 Ú x 1 x 2 ~ 1. 9. Выяснить, полна ли система функций: А = { xy, x Ú y, x Å y, xy Ú yz Ú zx }.
Литература 1. Гаврилов, Г. П. Задачи и упражнения по курсу дискретной математики: учеб. пособие / Г. П. Гаврилов, А. А. Сапоженко. – М.: Наука, 1992 – 408 с. 2. Горбатов, В. А. Фундаментальные основы дискретной математики / В. А. Горбатов. – М.: Наука, 2000. – 544 с. 3. Нефедов, В. Н. Курс дискретной математики: учеб. пособие / В. Н. Нефедов, В. А. Осипова. – М.: Изд-во МАИ, 1992. – 264 с. 4. Новиков, Ф. А. Дискретная математика для программистов: учебник для вузов / Ф. А. Новиков. – СПб.: Питер, 2001. – 304 с.
Практическое занятие № 11
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 339; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.72.252 (0.007 с.) |

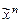 ) Î Т0 Û f(0, …, 0) = 0.
) Î Т0 Û f(0, …, 0) = 0.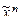 ) Î Т1 Û f(1, …, 1) = 1.
) Î Т1 Û f(1, …, 1) = 1.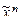 ) = f*(
) = f*(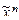 ).
).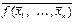 называется двойственной к f(
называется двойственной к f(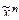 ), обозначается f*(
), обозначается f*(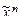 ), т. е. f *(
), т. е. f *(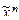 ) =
) = 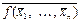 .
.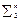 , таких, что a £ b Þ f(a) £ f(b).
, таких, что a £ b Þ f(a) £ f(b).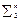 введем отношение порядка £, называемое отношением предшествования (отношением сравнимости), следующим образом: a £ b, если ai £ bi, i =
введем отношение порядка £, называемое отношением предшествования (отношением сравнимости), следующим образом: a £ b, если ai £ bi, i = 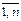 .
.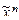 ) Î L Û f(
) Î L Û f(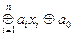 – представима полиномом Жегалкина не выше первой степени.
– представима полиномом Жегалкина не выше первой степени.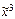 ) = (
) = ( ) = (1, 0, 0, 1, 0, 1, 1, 0) = f3(
) = (1, 0, 0, 1, 0, 1, 1, 0) = f3(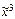 ), f4*(
), f4*(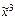 ) = (
) = (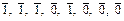 ) = (0, 0, 0, 1, 0, 1, 1, 1) = f4(
) = (0, 0, 0, 1, 0, 1, 1, 1) = f4( ) =
) = 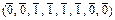 = (1, 1, 0, 0, 0, 0, 1, 1) ¹ f1(
= (1, 1, 0, 0, 0, 0, 1, 1) ¹ f1(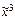 ) = (
) = (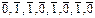 ) = (1, 0, 0, 1, 0, 1, 0, 1) ¹ f2(
) = (1, 0, 0, 1, 0, 1, 0, 1) ¹ f2(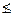 (1, 1, 0, 0), f2: (0, 1, 0, 1)
(1, 1, 0, 0), f2: (0, 1, 0, 1) 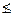 (0, 1, 1, 0), f3: (1, 0, 0, 1)
(0, 1, 1, 0), f3: (1, 0, 0, 1) 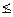 (0, 1, 1, 0); f4 Î М, т. к. f4: (0, 0, 0, 1) ≤ (0, 1, 1, 1); (0, 0) ≤ (0, 1) и (0,1) ≤ (1, 1); 0 ≤ 0 и 0 ≤ 1, и 1 ≤ 1.
(0, 1, 1, 0); f4 Î М, т. к. f4: (0, 0, 0, 1) ≤ (0, 1, 1, 1); (0, 0) ≤ (0, 1) и (0,1) ≤ (1, 1); 0 ≤ 0 и 0 ≤ 1, и 1 ≤ 1.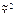 ) = (х 2 ® х 1)(х 2 ¯ х 2); б) f(
) = (х 2 ® х 1)(х 2 ¯ х 2); б) f(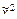 ) = (х 2 ~ х 1)(х 1| х 2);
) = (х 2 ~ х 1)(х 1| х 2);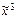 ) = (х 1 Å х 2) ® х 3)×ù(х 3 ® х 2);
) = (х 1 Å х 2) ® х 3)×ù(х 3 ® х 2); 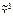 ) = (х 1 Ú х 2 Ú
) = (х 1 Ú х 2 Ú 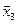 ) ® (х 1× х 2|
) ® (х 1× х 2| 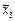 ) Å (х 2 ® х 1)×
) Å (х 2 ® х 1)× 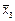 .
.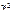 ) = ((х 2 Ú х 1) ® х 1× х 2 ) Å (х 1® х 2) Ù ( х 2 ® х 2);
) = ((х 2 Ú х 1) ® х 1× х 2 ) Å (х 1® х 2) Ù ( х 2 ® х 2);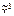 ) = (х 1 ® х 2 х 3)× (х 2 ® х 1 х 3) Ú (х 1 ~ х 2).
) = (х 1 ® х 2 х 3)× (х 2 ® х 1 х 3) Ú (х 1 ~ х 2). ) = (1, 0, 1, 0, 1, 0, 1, 0); б) f(
) = (1, 0, 1, 0, 1, 0, 1, 0); б) f(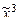 ) = (0, 1, 1, 0, 0, 1, 1, 0);
) = (0, 1, 1, 0, 0, 1, 1, 0); 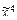 ) = (1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1);
) = (1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1); 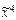 ) = (0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1).
) = (0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1).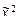 ) = (х 2 ® х 1)(х 2 ¯ х 2); б) f(
) = (х 2 ® х 1)(х 2 ¯ х 2); б) f(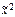 ) = (х 2 ~ х 1)(х 1| х 2);
) = (х 2 ~ х 1)(х 1| х 2);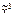 ) = (х 1 Å х 2) ® х 3)×ù(х 3 ® х 2);
) = (х 1 Å х 2) ® х 3)×ù(х 3 ® х 2); 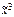 ) = (х 1 Ú х 2 Ú
) = (х 1 Ú х 2 Ú 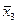 ) ® (х 1× х 2|
) ® (х 1× х 2| 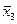 .
.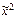 ) = ((х 2 Ú х 1) ® х 1× х 2) Å (х 1 ® х 2)(х 2 ® х 2);
) = ((х 2 Ú х 1) ® х 1× х 2) Å (х 1 ® х 2)(х 2 ® х 2);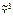 ) = (х 1 ® х 2 х 3)× (х 2 ® х 1 х 3) Ú (х 1 ~ х 2).
) = (х 1 ® х 2 х 3)× (х 2 ® х 1 х 3) Ú (х 1 ~ х 2). ) = (х 2 ~ х 1)(х 2 ¯ х 2); б) f(
) = (х 2 ~ х 1)(х 2 ¯ х 2); б) f(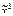 ) = (х 1Ú х 2|
) = (х 1Ú х 2| 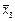 ) ® (х 2 ® х 1)×
) ® (х 2 ® х 1)× 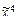 ) = (1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1); д) f(
) = (1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1); д) f(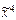 ) = (1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0).
) = (1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0).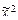 ) = (х 2 ~ х 1)(х 2 ¯ х 2); б) f(
) = (х 2 ~ х 1)(х 2 ¯ х 2); б) f(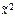 ) = (х 2 ® х 1)(х 1| х 2);
) = (х 2 ® х 1)(х 1| х 2);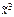 ) = (х 1 ~ х 2 Ú
) = (х 1 ~ х 2 Ú 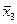 ) ® (х 1× х 2|
) ® (х 1× х 2| 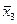 ) Å (х 2 ® х 1)×
) Å (х 2 ® х 1)× 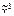 ) = (х 1 ® х 2 Å х 3)× (х 2 ® х 1 Ú х 3) Ú (х 1 ~ х 2).
) = (х 1 ® х 2 Å х 3)× (х 2 ® х 1 Ú х 3) Ú (х 1 ~ х 2).


