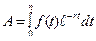Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Річна рента з платежами в середині періодівСодержание книги
Поиск на нашем сайте
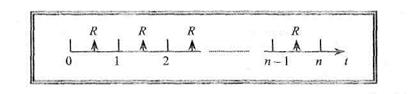
Аналіз фінансових потоків у різних сферах діяльності може суттєво різнитися. Так, орендні, податкові та митні платежі часто здійснюють на початку відповідного періоду, тому вони являють собою авансову ренту. Відсотки за депозитами та кредитами, дивіденди за акціями зазвичай нараховують наприкінці періоду, тому вони є звичайною рентою. Однак, у цілому, рентні платежі можуть надходити в будь-які моменти часу, а не лише на початку чи в кінці періоду. Наприклад, аналізуючи не фінансові, а виробничі інвестиції, можна побачити, що, за відсутності фактору сезонності, надходження і вилучення коштів на виробництві відбуваються майже рівномірно (а іноді — навіть постійно) протягом відповідного періоду (року, кварталу, місяця тощо). В такому разі доцільним є застосування рент з платежами, які здійснюють у середині періодів, оскільки обчислення саме за такою рентою дасть точніший результат. Розглянемо основні вартісні характеристики ренти з платежами, які здійснюють в середині періодів. Постійну скінчену річну ренту з платежами в середині періодів з параметрами { R,п, r } з погляду розташування платежів у часі графічно відображено на рис. 5.5.
Рис. 5.5. Постійна скінчена річна рента з платежами в середині періодів
На рис. 5.5 показано, що розмір періодичних платежів R = со nst, платежі в початковий (нульовий) та в останній (n -ний) момент часу не здійснюють, платежі надходять в середині відповідних періодів. Порівнявши графіки виплат, наведені на рис. 5.1, 5.4 та 5.5, можна зробити висновки, що фактично виплату для рент з платежами в середині періодів здійснюють на півперіоду раніше, ніж для звичайних рент та на півперіоду пізніше, ніж для авансових рент. Отже, за аналогією з рівнянням (5.11) для ренти з платежами в середині періодів можна записати таку формулу:
де S1/2 — нарощена сума ренти з платежами в середині періодів, Spost — нарощена сума ренти постнумерандо. Рівняння (5.17) дозволяє визначити майбутню вартість ануїтету з платежами в середині періодів за відомої майбутньої вартості звичайного ануїтету. Для визначення теперішньої вартості ануїтету з платежами в середині періодів, за відомої теперішньої вартості звичайного ануїтету, за аналогією з (5.15), можна записати співвідношення (5.18):
Таким чином, для обчислення початкової та кінцевої вартості скінченої ренти з платежами в середині періодів, спочатку зазвичай обчислюють вартісні характеристики для ідентичної ренти постнумерандо, а потім перемножують відповідні вартісні характеристики ренти постнумерандо на множник нарощування за половину періоду. Для оцінювання вартісних характеристик одразу для ренти з платежами в середині періодів необхідно скористатися формулою:
Рівняння (5.19) дозволяє визначити майбутню вартість ануїтету з платежами в середині періодів. Для оцінювання його теперішньої вартості запишемо рівняння (5.20):
Інші види фінансових рент Вище було висвітлено основні види річних рент (ануїтетів), які найбільш широко застосовують на практиці. Проте у загальному випадку будь-яка рента може передбачати р платежів за рік, при цьому проценти на них нараховують т разів на рік. Причому періодичність та кількість платежів р не обов'язково збігається з періодичністю та кількістю нарахувань процентів т. Зрозуміло, що у цьому разі питання оцінювання теперішньої та майбутньої величин таких рент значно ускладнюється. Розглянемо це питання на прикладі рент постнумерандо. Нехай скінчена рента постнумерандо передбачає р платежів за рік, при цьому проценти, нараховують т разів на рік. Подивимось, як видозміняться канонічні рівняння (5.4) та (5.6) залежно від кількості платежів та періодичності нарахувань процентів. Розглянемо наступні співвідношення. Загальний випадок — т ≠р У цьому випадку для нарощеної суми маємо:
Знаючи нарощену величину такої ренти, можна знайти її теперішню вартість з рівняння (5.22):
Розглянемо окремі випадки цієї ренти. Річна рента (р = 1) з нарахуванням процентів т разів за рік. Якщо проценти нараховують т разів на рік, а платежі річні, то нарощена сума дорівнює:
Теперішню величину такої ренти обчислюють за формулою (5.23). р - термінова рента з нарахуванням процентів один раз за рік (т = 1) Якщо платежі здійснюються декілька разів за рік, а проценти нараховують один раз за рік нарощена сума дорівнює:
Теперішню величину такої ренти розраховують за формулою (5.5). р — термінова рента з т =р Досить часто у фінансових обчисленнях припускають, що кількість платежів за рік та кількість нарахувань процентів збігаються (тобто т=р). Майбутня сума такої ренти дорівнює:
Теперішню величину цієї ренти обчислюють за формулою (5.23). Підставивши вираз (5.25) у рівняння (5.22) отримаємо:
Аналогічні рівняння можна вивести не лише для рент з платежами наприкінці періоду, а й для рент з платежами в довільний момент часу. Повертаючись до класифікації, наведеної в табл. 2.1, підкреслимо, що уточнюючи ще ряд параметрів, окрім періодичності платежів та нарахування процентів, можна отримати зовсім інші типи рент. Наприклад, було розглянуто лише постійні ренти, в яких величини всіх членів ренти однакові. Зрозуміло, що існують і змінні ренти з різними розмірами платежів. Причому в деяких випадках члени такої ренти змінюються за певними закономірностями. Наприклад, виокремлюють змінні ренти з постійним абсолютним приростом платежів (розміри членів ренти змінюються за арифметичною прогресією) та постійним відносним приростом платежів (за геометричною прогресією). Крім того, було розглянуто лише дискретні ренти, за якими платежі надходять через фіксовані проміжки часу. Але інколи потік платежів розглядають як неперервний процес. Найскладнішими в математичному плані є фінансові ренти, що описують неперервним змінним потоком платежів. На сьогодні, вони майже не застосовні на практиці, проте є окремим напрямом наукових досліджень. У фінансових обчисленнях, які стосуються таких потоків платежів, вважають, що коли потік неперервний, то розміри платежів у часі описуються функцією Тоді нарощену суму неперервного змінного потоку платежів, відповідно до введених раніше позначень, визначають так:
Відповідно, теперішня вартість такого потоку дорівнює:
Необхідно зазначити, що оскільки через потоки платежів описуються будь-які фінансові розрахунки в економіці, то розмаїття схем та механізмів фінансових операцій зумовлює появу безлічі інших видів фінансових рент.
ТЕМА 6 ОЦІНКА ТА ПЛАНУВАННЯ СХЕМ ФІНАНСОВО-КРЕДИТНИХ РОЗРАХУНКІВ 6.1. Застосування теорії рент у плануванні схем фінансово-кредитних розрахунків
Якщо фінансова операція передбачає не відокремлений (одноразовий) платіж, а певну послідовність платежів у часі, то для планування схеми таких розрахунків доцільно скористатися теорією фінансових рент.
Теорія фінансових рент — сучасна фінансова теорія, яка з'явилася порівняно недавно. Однак, можна стверджувати, що саме поява методології математичного дисконтування потоків платежів, значно розширило межі та можливості кількісного фінансового аналізу, зокрема дозволивши точніше враховувати вартість фінансових потоків у часі. Основні види фінансових рент та обчислення їх вартісних характеристик було наведено в попередньому розділі. Тепер, на підґрунті розглянутого вище фінансово-математичного апарату, доцільно розглянути існуючі у практиці схеми фінансово-кредитних розрахунків. Зазначимо, що фінансові обчислення щодо потоків платежів мають суто прикладний характер, визначаючи конкретні фінансові схеми розрахунків. Насамперед, у вигляді фінансових рент представляють різноманітні кредитні операції та відповідні схеми погашення заборгованостей. Сучасні економічні відносини передбачають, що переважна більшість суб'єктів господарювання для свого розвитку застосовують ті чи інші варіанти кредитування. Оптимізацію кредитних розрахунків, що полягає у пошуку зручних схем кредитних виплат, провадять на підґрунті аналізу відповідних потоків платежів. Розглянемо основні умови кредитування, які аналізують у теорії фінансових рент: — термін кредиту (позики); — метод (схема) погашення основної суми боргу та процентів; — рівень процентів за кредитом та метод нарахування процентів; — додаткові умови (пільговий період, можливості дострокового погашення, пролонгації, реструктуризації тощо). Зрозуміло, що фінансове навантаження щодо обслуговування боргу залежатиме від розміру та періодичності виплат, розміру першої виплати, принципів нарахування процентів на суму боргу та багатьох інших чинників. Визначення оптимальних умов кредитних розрахунків передбачає опис кредитних виплат у вигляді певного потоку платежів з подальшою оцінкою його вартісних характеристик. Причому, залежно від розподілу платежів у часі, буде відкориговано й інші параметри кредитної угоди. Таким чином, за допомогою операції математичного дисконтування можна знайти такий потік платежів, що забезпечуватиме оптимальне (прийнятне) фінансове навантаження для боржника відповідно до його виробничих циклів, оборотності коштів тощо. Отже, кількісний аналіз фінансових потоків платежів - основа проведення більшості кредитно-фінансових операцій, зокрема:
• лізингових операцій; • споживчого кредитування; • іпотечного кредитування; • орендних платежів з подальшим викупом майна; • амортизаційних відрахувань; • створення фондів нагромадження коштів; • в створення спеціальних фондів погашення боргу тощо. Крім того, за допомогою теорії фінансових рент визначають вартісні характеристики різних видів цінних паперів. Наприклад, вартісна оцінка акцій ґрунтується на моделях дисконтування дивідендів, а оцінка процентних облігацій передбачає дисконтування процентних (купонних) виплат. У цій темі розглянемо лише основні схеми фінансових розрахунків та відповідні співвідношення, які, мають найбільше прикладне значення. В цілому ж, сфера застосування теорії рент настільки широка й універсальна, що можна навіть стверджувати, що без її використання неможливо побудувати ефективну систему фінансового менеджменту будь-якого суб'єкта господарювання незалежно від напряму його діяльності.
|
||||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 103; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.201.169 (0.012 с.) |

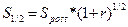 (5.17)
(5.17)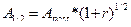 (5.18)
(5.18)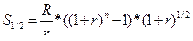 (5.19)
(5.19)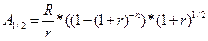 (5.20)
(5.20)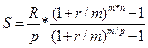 (5.21)
(5.21)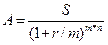 (5.22)
(5.22)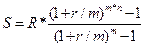 (5.23)
(5.23)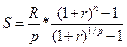
 (5.24)
(5.24)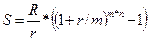 (5.25)
(5.25)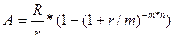
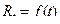 , а для нарахування процентів використовують процентну ставку у вигляді сили росту.
, а для нарахування процентів використовують процентну ставку у вигляді сили росту.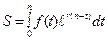 (5.26)
(5.26)