Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обчислення за правилом складних відсотків в умовах змін вихідних параметрівСодержание книги
Поиск на нашем сайте
За правилом складних процентів вартісні характеристики фінансової угоди (кінцева та початкова вартість коштів) безпосередньо залежатимуть від строку (кількості періодів) та норми дохідності фінансової операції. Проаналізуємо чутливість вартісних характеристик угоди до змін параметрів часу та дохідності. Класична формула нарощування складних процентів (3.1) передбачає, що протягом усіх періодів п ставка дохідності r є сталою величиною. Однак в реальних економічних умовах, ринкові ставки дохідності весь час змінюються, отже, у довгострокових фінансових угодах фіксувати ставку нарощування (або дисконтування) на весь термін угоди на визначеному початковому рівні не завжди доцільно. У разі плаваючих (змінних) ставок дохідності, зазвичай весь строк угоди розбивають на періоди, протягом яких ставка є незмінною. Таким чином, коли впродовж терміну угоди ставки дохідності змінюються в часі, але в певні терміни, то нарощену за складними процентами суму визначають за формулою:
де Т — загальна кількість періодів нарощування; r — ставка дохідності у періоді t; п, — тривалість t періоду, у якому ставка дохідності не змінюється. Для визначення середньої ставки дохідності складних процентів r за повний строк дії фінансової угоди N необхідно розв'язати відносно r таке рівняння:
звідси
Отже, множник нарощування за середньою ставкою складних процентів Окрім плаваючої ставки дохідності, іншим змінним вихідним параметром фінансової операції є загальна кількість періодів нарощування чи дисконтування. У практиці фінансових розрахунків часто трапляються ситуації, коли за фіксованого загального строку угоди п змінюється кількість періодів нарахувань коштів. Наприклад, за банківським депозитом вказується річна ставка складних процентів r, а нарахування здійснюють щомісяця чи щокварталу тощо. Отже, у деяких фінансових угодах капіталізація (нарахування) процентів відбувається т разів однаковими частками через однакові проміжки часу протягом кожного періоду часу t (t =1,…, n). В такому разі класична формула (3.1) для обчислення майбутньої вартості за правилом складних процентів, набуде вигляду:
де п — загальний строк угоди (кількість років чи інших періодів часу); т — кількість нарахувань процентів протягом одного періоду часу. Зазначимо, що коли т = 1 (тобто загальна кількість нарахувань процентів співпадає з загальною кількістю періодів), то вираз (3.14) повністю співпадатиме з виразом (3.1). Отже, класичну формулу нарощування складних процентів можна вважати частковим випадком рівняння (3.14). Приклад 3.3. Вкладник поклав на депозит у банк 1 тис. грн. під 16 % річних. Умовами угоди передбачено, що на цю суму банк нараховує складні проценти щокварталу. Треба знайти суму, що акумулюється на депозитному рахунку через рік. Рішення. За формулою (3.14) маємо:
Тобто, фактична річна дохідність банківського депозиту, завдяки щоквартальному нарахуванню коштів, становить близько 17 %. Якщо б нарахування за річною ставкою в 16 % відбулося лише один раз на рік, то на депозитному рахунку була б менша сума— 1,16 тис. грн. Таким чином, коли виплати здійснюють за правилом складних процентів кілька разів на рік, то фактична річна дохідність фінансової угоди більша від задекларованої річної дохідності за рахунок реінвестування коштів. Зазначимо, що за правилом простих процентів фактична дохідність угоди завжди співпадатиме із задекларованою дохідністю, оскільки проценти нараховують лише на початкову суму (не реінвестуються), отже нарощена величина не залежатиме від кількості нарахувань протягом одного періоду часу.
|
||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 94; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.222.132 (0.01 с.) |

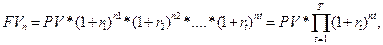 (3.12)
(3.12)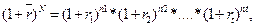
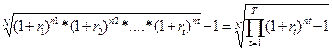 (3.13)
(3.13)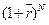 визначають за формулою зваженої середньої геометричної величини.
визначають за формулою зваженої середньої геометричної величини.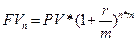 (3.14)
(3.14)