
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Київський національний економічний університетСтр 1 из 19Следующая ⇒
КИЇВСЬКИЙ НАЦІОНАЛЬНИЙ ЕКОНОМІЧНИЙ УНІВЕРСИТЕТ ІМ. В. ГЕТЬМАНА КРИВОРІЗЬКИЙ ЕКОНОМІЧНИЙ ІНСТИТУТ
Кафедра фінансів
ФІНАНСОВІ РОЗРАХУНКИ КОНСПЕКТ ЛЕКЦІЙ
(для спеціальності 6.508 „Фінанси”)
Зміст
Тема 1 Концептуальні засади фінансових розрахунків Час як фактор вартості
В практичних фінансових операціях гроші незалежно від їх призначення або походження обов’язково пов’язуються з конкретними моментами або періодами часу. Для цього в контрактах фіксуються відповідні строки, дати, періодичність грошових виплат. Фактор часу, особливо у довгострокових операціях, відіграє не менш важливу, іноді, навіть, більшу роль, ніж розмірі грошових сум. Необхідність врахування часового фактору виходить із суті фінансування та кредитування і відображається у принципі нерівноцінності грошей, що відносяться до різних періодів часу. Очевидно, що 1000 грн., отримані через 5 років, нерівноцінні цій же сумі, отриманій сьогодні, навіть, якщо не приймати до уваги інфляцію та ризик їх неотримання (Час-Гроші). Значущість фактора часу в комерційних і фінансових операціях обумовлена: - продуктивністю використання в часі коштів як фінансового активу, що приносить дохід; - наявністю й рівнем інфляційних процесів, які ведуть до знецінення грошей у часі; - невизначеністю майбутнього й пов'язаним із цим ризиком неотримання доходу.
Нерівномірність грошей у часі викликає: - необхідність обліку фактора часу при проведенні фінансових операцій і оцінці фінансових результатів виробничо-господарської й підприємницької діяльності; - некоректність з погляду довгострокових фінансових операцій сумування грошових величин, що відносяться до різних періодів часу.
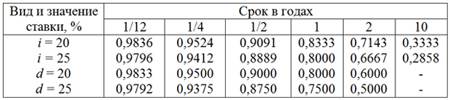
Дисконтні множники
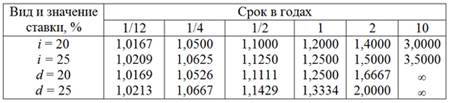
Таблиця 1.3 Множники нарощення
Дані таблиць 1.2, 1.3 наочно свідчать про чутливість фінансових і комерційних операцій до фактора часу. З даних таблиць видно, що вплив цього фактора підсилюється при збільшенні розміру ставки, як для операцій нарощення, так і для дисконтування. У процесі аналізу інвестиційних рішень прийнято використовувати складні відсотки. Складний відсоток характеризує суму доходу, яка утворюється в результаті інвестування грошей за умови, що сума нарахованого простого відсотка (r) не виплачується наприкінці кожного періоду, а приєднується до суми основного внеску (PV) і в наступному платіжному періоді (n) сама приносить дохід, капіталізується. Майбутнє значення вартості грошей (FV) має вигляд (формула 1.1):
Теперішнє значення вартості майбутньої суми грошей має значення (формула 1.2):
Оскільки процес інвестування має, як правило, більшу тривалість, у практиці аналізу ефективності капітальних вкладень доводиться мати справу не з одиничними грошовими сумами, а з потоками коштів. Обчислення нарощеної та дисконтованої оцінок коштів у цьому випадку здійснюється для кожного елемента грошового потоку. Зміна вартості грошей у часі пов'язана з об'єктивними умовами здійснення відтворювального процесу в економічній системі, який завжди супроводжується тими або іншими змінами вартості. Чим швидше здійснюється відтворювальний процес, тим швидше змінюється вартість грошей і навпаки. Збільшення вартості валового внутрішнього продукту приводить до зміни грошової маси в обігу, необхідної для його обслуговування. Отже, об'єктивною основою зміни вартості грошей у часі виступає результат відтворювального процесу. Однак найчастіше ці зміни зв'язують із інфляцією або з ризиком не одержання або неповної суми одержання доходів у вигляді дивідендів або відсотків на вкладений капітал. У цьому випадку вартість грошей у часі розглядають як деякий механізм порівняння різних видів вкладень і доходів. У практиці фінансових і комерційних операцій такий підхід вважають цілком виправданим, тому що фактор часу, особливо в довгострокових фінансових операціях або в умовах нестабільної економічної ситуації має більше значення, ніж розміри вкладених або одержуваних грошових сум. Таким чином, при здійсненні довготривалих фінансових операцій фактор часу відіграє важливу роль у практиці укладених угод і викликає необхідність його обліку шляхом порівняння й оцінки вартості грошей на початку фінансової операції й при їхньому поверненні у вигляді майбутніх грошових надходжень. Вплив фактора часу підсилюється інфляційними процесами й вимагає додаткових розрахунків. При визначенні ефективності угод просте підсумовування грошових величин, що відносяться до різних періодів часу, не припустиме. Для цього необхідно використовувати приведення економічних величин (доходів, прибутків, витрат) з різних тимчасових періодів до обраного моменту або інтервалу часу (до початку або до кінця розглянутого періоду). Облік фактора часу дає можливість, не тільки рівно привести тимчасові доходи й витрати комерційної й фінансової діяльності до порівнянного виду, але й оцінити їх динаміку на основі побудови й аналізу вартісно-тимчасових залежностей.
ТЕМА 2 Прості відсотки ТЕМА 3 СКЛАДНІ ВІДСОТКИ Рис. 3.1. Графік зростання вартості за правилом складних процентів
Із наведеного графіка видно, що нарощування вартості в часі за складними процентами є показниковоюфункцією. Криві прибутковості Будь-яка позичкова або кредитна операція припускає використання процентної ставки, з якою погодилися обидві сторони, що брати участь в операції. Як уже зазначалося вище, значення ставки залежить від багатьох факторів. Для практика важливо уявити собі закономірність зміни розміру ставок залежно від певного фундаментального фактору. Імовірно, найбільш важливим з таких факторів є ризик неповернення позички. Очевидно, що подібного роду ризик залежить від ряду факторів, серед яких, в свою чергу, важливим є строк операції. Так, при всіх інших рівних умовах позичка на п'ять років є більш ризикованою, ніж, скажімо, на два роки. Компенсувати ризик власникові грошей може підвищення прибутковості. Таким чином, залежність „прибутковість — ризик” приблизно можна охарактеризувати за допомогою залежності „прибутковість — строк”, одержати яку для практичних цілей суттєво простіше. Таку залежність, представлену у вигляді графіка, називають кривої прибутковості (рис.3.2).
Рис. 3.2. Криві прибутковості t
На графіку по вертикалі відкладають прибутковість (Y), по горизонталі — строк (t). Якщо графік охоплює широкий діапазон строків (як короткострокові, так і довгострокові операції), то для виміру строку застосовують логарифмічну шкалу. Спостережувані значення прибутковості звичайно перебувають близько кривої або безпосередньо на ній.
Отже, крива прибутковості характеризує зміну прибутковості однорідних кредитно-позичкових операцій або фінансових інструментів (наприклад, довгострокових облігацій, акцій компаній і т.д.) залежно від їхнього строку. Конкретна крива прибутковості відповідає реальної ситуації, що склалася на грошово-кредитному ринку, і характерна для короткого тимчасового періоду. Зміна ситуації змінює форму кривої та її положення на графіку. Для нормальних економічних умов крива прибутковості має форму кривої Ана рис. 3.2. Прибутковість зростає в міру збільшення строку інвестицій. Причому кожна наступна одиниця приросту строку дає все менше збільшення прибутковості. Таку криву називають позитивною, або нормальною, кривою прибутковості. Нормальна форма кривої спостерігається в умовах, коли інвестори враховують такі фактори, як скорочення ступеня ліквідності й зростання невизначеності фінансових результатів при збільшенні строку. Крива прибутковості, близька до горизонтальної прямої (крива Б на рис. 3.2), вказує на те, що інвестори не беруть до уваги або в малому ступені враховують ризик, пов'язаний зі строком. Іноді зустрічаються „негативні” і „згорблені” криві прибутковості. Перша відповідає зменшенню прибутковості в міру збільшення строку (нестабільність фінансового ринку), друга — падінню прибутковості після періоду деякого її росту. Існують дві конкуруючі (а іноді доповнюючі) теорії, що пояснюють „поведінку” прибутковості — теорія ліквідності й теорія очікувань. Перша зміну прибутковості пов'язує зі збільшенням ризику ліквідності в міру збільшення строку. Саме із цієї позиції пояснюються вище позитивна й горизонтальна криві прибутковості. Згідно із другою теорією стверджується, що форма кривої може розглядатися і як узагальнена характеристика очікувань інвесторів, вірніше, їхньої поведінки в теперішній момент у зв'язку з очікуваннями змін процентних ставок у майбутньому. Однак інтерпретація форми кривої у цьому плані неоднозначна, та й не може бути іншою, оскільки доводиться брати до уваги принаймні дію двох факторів — ризику й очікування змін ставок. Наприклад, позитивна крива іноді може інтерпретуватися як вказівка на те, що інвестори очікують зростання ставок у майбутньому. Однак частіше ця ж форма кривої вважається симптомом відносної стабільності грошово-кредитного ринку. Криві прибутковості одержали поширення як інструмент, що допомагає при розв'язку ряду інвестиційних проблем. Зокрема, при порівнянні прибутковості різних фінансових інструментів (сполучення на одному графіку декількох кривих прибутковості), корегуванню портфеля активів тощо. Приклад 3.4. Розглянемо на прикладі один із простих способів застосування кривої прибутковості. Припустимо, необхідно інвестувати деяку суму грошей на чотири роки. Причому, у інвестора є тільки два варіанти для цього: розмістити цю суму на депозиті відразу на весь строк або спершу на три роки, а потім на один рік. Нехай рівні процентних ставок відносяться до нормальної кривої прибутковості: по трирічних депозитах — 10%, по чотирирічним — 10,5% складних річних. Розмір ставки для депозиту на один рік (тобто на четвертий рік) у момент ухвалення рішення, невідомий. Який варіант розміщення коштів повинен вибрати інвестор?
Рішення. Очевидно, що при виборі другого варіанта інвестор повинен мати результат не гірше, ніж при першому варіанті. Завдання, отже, зводиться до визначення того значення ставки для четвертого року, при якому обидва варіанти будуть рівноцінними (еквівалентними) у фінансовім відношенні. Назвемо таку ставку критичною, або бар'єрною. Позначимо як i3 і і4 рівні процентних ставок для депозитів на три й чотири роки, а через і0 — невідому критичну ставку для річного депозиту. В силу фінансової еквівалентності результатів розміщення коштів множники нарощення для обох варіантів повинні бути рівними один одному. Звідси:
а, відповідно,
За даними прикладу знайдемо критичну ставку:
Таким чином, для того щоб інвестор зупинився на другому варіанті, він повинен очікувати, що через три роки ставка за однорідними депозитами буде не менш 12,014 %, тобто рівень ставок підвищиться. Відповідно, якщо він очікує, що ставка не досягне цього рівня, слід обрати перший варіант. ТЕМА 4 ФІНАНСОВА ЕКВІВАЛЕНТНІСТЬ Рис. 4. 1. Графік множників нарощування вартості за правилами простих та складних процентів З рис. 4.1 неважко побачити, що на проміжку t є (0;1) більшими є значення функції множника нарощування простих процентів, а на проміжку t є (1;n ), навпаки — значення функції, що відповідає правилу складних процентів. Графіки функцій множників нарощування перетинаються лише один раз при t = 1. Тобто, еквівалентність (рівність) множників нарощування простих та складних процентів, за умови однакових параметрів r та п, досягається лише за одноразового нарощування коштів. Дійсно, за умов r іс = ris = r та t =1: В цілому, порівнюючи множники нарощування простих та складних процентів можна зробити відповідні висновки. Якщо взяти однакові за величиною, але різні за правилом нарощування процентів річніставки нарощування, то: · для строку меншогоза один рік вартість нарощується швидше за правилом простихпроцентів, тобто:
· для строку більшого,ніж один рік вартість нарощується швидше за правилом складнихпроцентів, тобто
· для строку t=1рік множники нарощування дорівнюють
Оскільки у комерційних розрахунках тип множників нарощування зазвичай вибирають відповідно з принципами максимізації прибутку, то існує правило — у короткострокових фінансових угодах (строк менший за 1 рік) нарощування краще здійснювати за простими процентами, а у довгострокових — за складними процентами. Рис. 4.2. Графік множників утримання вартості за правилами простих та складних процентів
Зазначимо, що хоча обидві функції, зображені на рис. 4.2, є спадними, їхня область існування обмежена проміжком [0;1], що в свою чергу накладає певні обмеження на допустимі значення параметрів d та п. Зрозуміло, що кут нахилу цих функцій залежить від величини ставки утримання d. Чим більша ця ставка, тим швидше зменшується вартість у часі, і тим крутіший нахил відповідної функції. З рис. 4.2 неважко побачити, що на проміжку t є (0;1) більшими є значення функції множника утримання простих процентів, а на проміжку t є (1;n), навпаки — значення функції множника утримання складних процентів. Графіки функцій множників утримання перетинаються лише один раз при t=1. Тобто, еквівалентність (рівність) множників утримання простих та складних процентів, за умови однакових параметрів r та п, досягається лише за одноразового утримання коштів. Дійсно, за умов d іс = dis = d та t =1: Стосовно множника утримання складних процентів також необхідно підкреслити, що зі збільшенням кількості періодів п темп спадання вартості значно уповільнюється. Саме тому, у практиці фінансових обчислень методику утримання складних процентів рідко застосовують для великої кількості періодів. Як правило, кількість періодів утримання не перевищує 2-3. В цілому, порівняння множників утримання простих та складних процентів дає змогу зробити відповідні висновки. Якщо взяти однакові за величиною, але різні за правилом нарощування процентів річніоблікові ставки, маємо: · для строку меншогоза один рік спадання (утримання) вартості
· для строку більшого,ніж один рік спадання (утримання) вартості відбувається швидше за правилом простихпроцентів, тобто:
· для строку t = 1 рік множники утримання дорівнюють один
Нагадаємо, що взагалі операція утриманняпроцентів має обмежену сферу застосування, тобто обліковіставки (d) не так поширені, як ставки дисконтування (r). Проте, якщо комерційні розрахунки передбачають застосування облікових ставок, то, відповідно принципам максимізації прибутку, рекомендовано дотримуватися правила — у короткострокових фінансових угодах (строк менший за 1 рік) утримання здійснювати за складними процентами, а у довгострокових — за простими процентами. ТЕМА 5 Рис. 5.1. Постійна скінчена річна рента постнумерандо
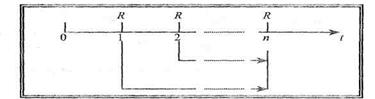
На рис. 5.1 показано, що розмір періодичних платежів R = со nst, платіж у початковий (нульовий) момент часу не здійснюють, платежі надходять наприкінці періодів з 1-го по останній (n -ний). Для того, щоб знайти нарощену величину такої ренти, необхідно всі періодичні платежі привести (наростити) до останнього періоду часу з урахуванням ставки r. Ілюструє операцію нарощування постійної скінченої річної ренти постнумерандо рис. 5.2.
Рис. 5.2. Нарощування звичайного ануїтету у часі Відповідно до наведеної на рис. 5.2 схеми, нарощена сума п членів звичайного ануїтету становитиме:
Числова послідовність є геометричною прогресією з першим членом, що дорівнює R та темпом росту (1+ r). Скориставшись формулою суми геометричної прогресії вираз (5.3) можна спростити так:
Величину ((1+ r) n -1)/ r, яка входить до складу рівняння (5.4), називають множником нарощування звичайного ануїтету (Future Value Interest Factor Annuities, FVIFA).
Розглянемо основні засади оцінювання початкової (дисконтованої) вартості звичайного ануїтету. Ілюструє операцію дисконтування постійної скінченої річної ренти постнумерандо рис. 5.3.
Рис. 5.3. Дисконтування звичайного ануїтету у часі Відповідно до наведеної на рис. 5.3 схеми, приведена (дисконтована) сума п членів звичайного ануїтету становитиме:
Отримане рівняння взаємозв'язку (5.5) між теперішньою та кінцевою величинами звичайного ануїтету повністю відповідає загальній властивості грошових потоків (5.2). Підставивши вираз (5.4) у рівняння (5.5), отримаємо:
Величину (1-(1+ r)- n / r, яка входить до складу рівняння (5.6), називають множником дисконтування звичайного ануїтету (Present Value Interest Annuities, PVIFA). Для підвищення ефективності розрахунків в умовах відсутності засобів обчислювальної техніки, для множників нарощування та дисконтування звичайних ануїтетів існують спеціальні довідкові фінансові таблиці. Таким чином, користуючись рівняннями (5.4) і (5.6'), знаючи три параметри: розмір щорічного платежу R, кількість років п та ставку дохідності r, завжди можна знайти теперішню та майбутню величини звичайного ануїтету. При плануванні схем погашення боргу, часто розв'язують обернену задачу — за відомої теперішньої або майбутньої величини боргу та необхідної ставки дохідності, оцінюють розмір щорічного платежу за кредитом, залежно від строку кредиту. Розв'яжемо рівняння (5.4) і (5.6) відносно величини щорічного платежу R.. За відомої кінцевої величини звичайного ануїтету маємо:
Відповідно, за відомої початкової величини звичайного ануїтету отримаємо:
Отримані вирази (5.7) та (5.8) дозволяють оцінити необхідну величину щорічного платежу за кредитною угодою та дозволяють її коригувати залежно від строку, суми боргу, ставки по кредиту тощо. Навівши основні рівняння щодо вартісних характеристик звичайного ануїтету, для кращого розуміння сутності ануїтет них платежів, розглянемо як відбувається нарощення ануїтету по роках. Приклад. Маємо звичайний ануїтет з такими параметрами: строк ренти n=5 років, річний платіж R=1000 грн., ставка дисконтування r=10%. Знайти нарощені суми наприкінці кожного року. Рішення. Насправді механізм нарахування ренти простий. До суми, що була на рахунку на початок періоду, додається річний платіж. У результаті отримуємо суму на кінець періоду. Потім на останню нараховуємо складний процент. Отримана величина – це сума на початок наступного періоду. Далі цикл повторюється до закінчення строку ренти. Розрахунки наведено нижче в таблиці.
Отже, нарощена сума становить 6105,1 грн., а теперішня величина ренти за формулою (5.5) дорівнює 6105,1/1,15=3791 грн. Нескінчена рента постнумерандо (перпетуїтет) Розглядаючи ренти постнумерандо, необхідно окремо зупинитися на так званій „ вічній” (нескінченій) ренті. Нескінчена рента (перпетуїтет) — це рента, послідовність платежів за якою нескінчена, тобто вважається, що така рента буде виплачуватися необмежено довго. Аналіз часткового випадку рівнянь (5.4) та (5.6) за умов, що п →∞, дає змогу зробити висновки стосовно вартісних характеристик перпетуїтету. Нарощена величина S нескінченої ренти теж прямує до нескінченості, а теперішню величину нескінченої ренти знаходять з рівняння (5.9):
З виразу (5.9) видно, що теперішня вартість нескінченої ренти залежить лише від розміру щорічного платежу та річної ставки дохідності. Причому припускається, що ринкова дохідність r з плином часу залишається незмінною. Приклад 5.1. Компанія орендує приміщення за 60 тис. грн. на рік. Чому дорівнює викупна ціна оренди, якщо річна ставка ринкової дохідності складає 15 %? Рішення. Викупна ціна — це теперішня величина всіх майбутніх орендних платежів. За формулою (5.9) вона дорівнює: А = 60 / 0,15 = 400 тис. грн. Неважко побачити, що при збільшенні річної ставки до 20 % викупна ціна становитиме лише 300 тис. грн., тобто номінальну (недисконтовану) суму п'ятирічних орендних платежів. Зазначимо, що згідно виразу (5.9), при збільшенні ринкової норми дохідності теперішня вартість нескінченої ренти буде зменшуватися, тобто строк окупності капіталовкладень буде коротший.
Рис. 5.4. Постійна скінчена річна рента пренумерандо На рис. 5.4 показано, що розмір періодичних платежів R = со nst, перший платіж здійснюють в початковий (нульовий) момент часу, платежі надходять на початку періодів, тобто в останній (n -ний) момент часу платіж не здійснюють. Порівнявши графіки виплат, наведені на рис. 5.1 та 5.4, можна зробити висновки, що фактично виплату для авансових рент здійснюють на один період раніше, ніж для звичайних рент. Відповідно до введених раніше позначень, запишемо вираз (5.10) для нарощеної суми п- членів авансового ануїтету:
Порівнявши вирази (5.3) та (5.10), можна вивести наступне співвідношення нарощених сум для звичайних та авансових рент:
де З рівняння (5.11) видно, що для авансового ануїтету, з погляду нарахування процентів, кожний член ренти „спрацьовує” на один раз більше, ніж для звичайного ануїтету. Врахувавши властивість (5.11) у формулі (5.4), можна записати таке рівняння для знаходження нарощеної вартості авансового ануїтету:
Вираз (5.12) доцільно використовувати у разі наявності довідкових фінансових таблиць множників нарощування звичайних ануїтетів. Тоді для визначення нарощеної вартості авансового ануїтету значення з фінансової таблиці достатньо помножити на (1+ r). Розглянемо питання оцінювання теперішньої вартості авансового ануїтету. Відповідно до наведеної на рис. 5.4 схеми, приведена (дисконтована) сума п- членів скінченої ренти пренумерандо становитиме:
Зрозуміло, що для авансових рент, так само як і для інших видів рент, виходячи із загальної властивості грошових потоків (5.2), можна записати формулу:
Вираз (5.14) пов'язує між собою теперішню та кінцеву вартість авансового ануїтету. Для визначення теперішньої вартості авансового ануїтету за відомої теперішньої вартості звичайного ануїтету, за аналогією з (5.11), можна записати співвідношення (5.15):
Врахувавши властивість (5.15) у формулі (5.6), можна записати таке рівняння для знаходження теперішньої вартості авансового ануїтету:
Отриманий вираз (5.16) є досить складним, проте у разі наявності довідкових фінансових таблиць множників дисконтування звичайних ануїтетів, для визначення теперішньої вартості авансового ануїтету значення з фінансової таблиці достатньо помножити на (1+ r). Рис. 5.5. Постійна скінчена річна рента з платежами в середині періодів
На рис. 5.5 показано, що розмір періодичних платежів R = со nst, платежі в початковий (нульовий) та в останній (n -ний) момент часу не здійснюють, платежі надходять в середині відповідних періодів. Порівнявши графіки виплат, наведені на рис. 5.1, 5.4 та 5.5, можна зробити висновки, що фактично виплату для рент з платежами в середині періодів здійснюють на півперіоду раніше, ніж для звичайних рент та на півперіоду пізніше, ніж для авансових рент. Отже, за аналогією з рівнянням (5.11) для ренти з платежами в середині періодів можна записати таку формулу:
де S1/2 — нарощена сума ренти з платежами в середині періодів, Spost — нарощена сума ренти постнумерандо. Рівняння (5.17) дозволяє визначити майбутню вартість ануїтету з платежами в середині періодів за відомої майбутньої вартості звичайного ануїтету. Для визначення теперішньої вартості ануїтету з платежами в середині періодів, за відомої теперішньої вартості звичайного ануїтету, за аналогією з (5.15), можна записати співвідношення (5.18):
Таким чином, для обчислення початкової та кінцевої вартості скінченої ренти з платежами в середині періодів, спочатку зазвичай обчислюють вартісні характеристики для ідентичної ренти постнумерандо, а потім перемножують відповідні вартісні характеристики ренти постнумерандо на множник нарощування за половину періоду. Для оцінювання вартісних характеристик одразу для ренти з платежами в середині періодів необхідно скористатися формулою:
Рівняння (5.19) дозволяє визначити майбутню вартість ануїтету з платежами в середині періодів. Для оцінювання його теперішньої вартості запишемо рівняння (5.20):
Інші види фінансових рент Вище було висвітлено основні види річних рент (ануїтетів), які найбільш широко застосовують на практиці. Проте у загальному випадку будь-яка рента може передбачати р платежів за рік, при цьому проценти на них нараховують т разів на рік. Причому періодичність та кількість платежів р не обов'язково збігається з періодичністю та кількістю нарахувань процентів т. Зрозуміло, що у цьому разі питання оцінювання теперішньої та майбутньої величин таких рент значно ускладнюється. Розглянемо це питання на прикладі рент постнумерандо. Нехай скінчена рента постнумерандо передбачає р платежів за рік, при цьому проценти, нараховують т разів на рік. Подивимось, як видозміняться канонічні рівняння (5.4) та (5.6) залежно від кількості платежів та періодичності нарахувань процентів. Розглянемо наступні співвідношення. Загальний випадок — т ≠р У цьому випадку для нарощеної суми маємо:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 77; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.140.5 (0.219 с.) |
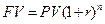 (1.1)
(1.1)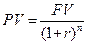 (1.2)
(1.2)
 Y A
Y A Б
Б

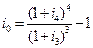

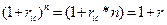 , що відповідає множнику нарощування для одноразового нарощування коштів.
, що відповідає множнику нарощування для одноразового нарощування коштів.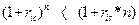 ;
;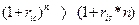 ;
;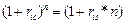
 , що відповідає множнику утримання для одноразового утримання (зменшення) вартості. Також зазначимо, що при строку t більшому за одиничний період, темп зменшення вартості за правилом простих процентів набагато швидший. Так, за правилом утримання простих процентів вартість зменшується до нуля в кінцевому періоді часу п = 1/ dis. Наприклад, за ставки dis = 20 %, множник утримання простих процентів, а отже, й кінцева вартість дорівнюватимуть нулю вже через 5 періодів часу. При цьому, множник утримання складних процентів, за тих самих умов, дорівнюватиме Dis 5;20% = 0,32768.
, що відповідає множнику утримання для одноразового утримання (зменшення) вартості. Також зазначимо, що при строку t більшому за одиничний період, темп зменшення вартості за правилом простих процентів набагато швидший. Так, за правилом утримання простих процентів вартість зменшується до нуля в кінцевому періоді часу п = 1/ dis. Наприклад, за ставки dis = 20 %, множник утримання простих процентів, а отже, й кінцева вартість дорівнюватимуть нулю вже через 5 періодів часу. При цьому, множник утримання складних процентів, за тих самих умов, дорівнюватиме Dis 5;20% = 0,32768. ;
;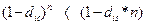 ;
;
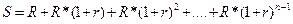 (5.3)
(5.3)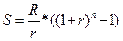 (5.4)
(5.4)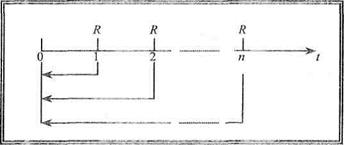
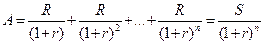 (5.5)
(5.5)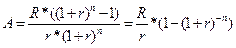 (5.6)
(5.6)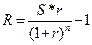 (5.7)
(5.7)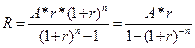 (5.8)
(5.8)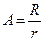 (5.9)
(5.9)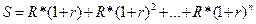 (5.10)
(5.10)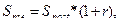 (5.11)
(5.11) — нарощена сума ренти пренумерандо,
— нарощена сума ренти пренумерандо, 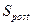 — нарощена сума ренти постнумерандо.
— нарощена сума ренти постнумерандо. (5.12)
(5.12)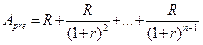 (5.13)
(5.13) (5.14)
(5.14)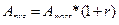 (5.15)
(5.15) (5.16)
(5.16)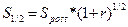 (5.17)
(5.17)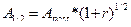 (5.18)
(5.18)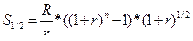 (5.19)
(5.19)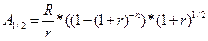 (5.20)
(5.20)


