
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предел последовательности. Геометрический смысл предела.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть каждому Число xn –элемент последовательности.
Пример 17.2. 1) 2)
Если xn=const, то последовательность называется постоянной.
Последовательность {xn} ограничена, если
Определение 17.3. Число а называется пределом числовой последовательности {xn}, если для любого положительного числа ε существует номер N такой, что при всех n>N выполняется неравенство
Обозначение: Последовательность, имеющая предел называется сходящейся, не имеющая его – расходящейся.
Пример 17.3. Определить предел последовательности (Ответ: Геометрический смысл предела числовой последовательности Число a – предел последовательности xn, если в любую окрестность числа а, начиная с некоторого номера попадают все члены последовательности
Пример 17.4. Показать, что последовательность Выберем интервал
Основные свойства сходящихся последовательностей
Теорема 17.2. Если последовательность {xn} имеет предел, то он единственный.
Доказательство Пусть {xn} имеет два предела a и b. Накроем их интервалами(c,d) и (e,f) (т.е.
Теорема 17.3. Если последовательность {xn} сходится, то она ограничена. Доказательство Пусть Известно, что
поэтому
Пусть тогда очевидно, что
Арифметические действия над последовательностями, имеющими предел
Замечание 1. Пусть Действительно, Это значит, что любой элемент последовательности {xn}, имеющей пределом число
Замечание 2. Произведение бесконечно малой последовательности на число есть бесконечно малая последовательность. Замечание 3. Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность. Замечание 4. Так как
Теорема 17.4. Если существуют конечные пределы последовательностей 1) 2) 3)
Доказательство Идея доказательства построена на неравенстве:
Пусть 1) 2) 3)
|
||||
|
Последнее изменение этой страницы: 2019-12-15; просмотров: 3131; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.94.221 (0.006 с.) |

 по некоторому закону поставлено в соответствие действительное число xn. Тогда говорят, что определена последовательность чисел x1,x2,…,xn или {xn}.
по некоторому закону поставлено в соответствие действительное число xn. Тогда говорят, что определена последовательность чисел x1,x2,…,xn или {xn}. ;
; .
. .
. .
.
 или
или  .
.
 .
. .)
.) .
. не имеет предела. Действительно, пусть а – предел xn..
не имеет предела. Действительно, пусть а – предел xn.. с длиной
с длиной  . Расстояние между -1 и 1 равно 2 и, следовательно, они оба не могут попадать в этот интервал.
. Расстояние между -1 и 1 равно 2 и, следовательно, они оба не могут попадать в этот интервал. ) Т.к. a=lim xn , то все элементы {xn} начиная с некоторого номера лежат в (c,d) и значит это противоречит тому, что b – предел.
) Т.к. a=lim xn , то все элементы {xn} начиная с некоторого номера лежат в (c,d) и значит это противоречит тому, что b – предел. . Зададим
. Зададим  . Тогда
. Тогда  :
:  .
.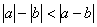 ,
, <1
<1 .
. ,
, .
.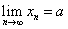 , тогда
, тогда  - бесконечно малая последовательность.
- бесконечно малая последовательность. .
. , можно представить в виде:
, можно представить в виде: (17.1).
(17.1). , то
, то  .
. , то справедливы равенства:
, то справедливы равенства: (17.2)
(17.2) (17.3)
(17.3) если
если  (17.4).
(17.4). .
. . Тогда согласно равенству (17.1):
. Тогда согласно равенству (17.1): - бесконечно малая последовательность (согласно 17.1);
- бесконечно малая последовательность (согласно 17.1); (бесконечно малая последовательность);
(бесконечно малая последовательность); (бесконечно малая последовательность).
(бесконечно малая последовательность).


